1736019749.png)
جواب فعالیت صفحه 36 درس 2 حسابان دوازدهم (مثلثات)
تعداد بازدید : 78.77Mپاسخ فعالیت صفحه 36 حسابان دوازدهم
-گام به گام فعالیت صفحه 36 درس مثلثات
-فعالیت صفحه 36 درس 2
-شما در حال مشاهده جواب فعالیت صفحه 36 حسابان دوازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
1 چند زاویه را که مقدار سینوس آنها برابر \(\frac{1}{2}\) است مثال بزنید.
\(\frac{\pi }{6}\,,\,\frac{{5\pi }}{6}\,,\,\frac{{13\pi }}{6}\,,\,\frac{{17\pi }}{6}\)
2 خط \(y = \frac{1}{2}\) و نمودار y=sinx را در زیر رسم کرده ایم. مقادیری را که مثال زده اید روی نمودار پیدا کنید. این مقادیر متناظر با چه نقاطی از شکل زیر می باشند؟
آیا مقادیری که پیدا کرده اید در بین نقاط نمایش داده شده در زیر هستند؟
A و B
بله.
3 طول تعدادی از نقاط تقاطع دو نمودار \(y = \frac{1}{2}\) و y=sinx را که در شکل فوق مشخص شده اند، در معادله \(\sin x = \frac{1}{2}\) جایگذاری کنید. آیا در معادله صدق می کنند؟ چه نتیجه ای می گیرید؟
\(\begin{array}{l}\sin \frac{\pi }{6} = \frac{1}{2}\\\sin \frac{{5\pi }}{6} = \sin (\pi - \frac{\pi }{6}) = \frac{1}{2}\\\sin - \frac{{7\pi }}{6} = \sin ( - \pi - \frac{\pi }{6}) = \frac{1}{2}\end{array}\)
بله؛ همگی صدق می کنند؛ نتیجه ای که می گیریم این است که تمامی نقاطی که از برخورد دو نمودار بدست می آیند، در معادله صدق می کنند.
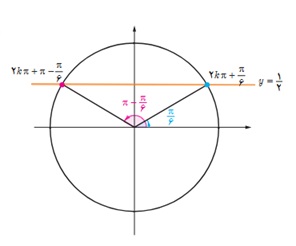
4 در دایره مثلثاتی زیر خط \(y = \frac{1}{2}\) و زوایای \(\pi - \frac{\pi }{6}\;,\;\frac{\pi }{6}\) که سینوس آنها برابر \(\frac{1}{2}\) است رسم شده اند. کدام دسته از زوایای مشخص شده بر روی نمودار سؤال قبل هم انتها با زاویه \(\frac{\pi }{6}\) و کدام دسته هم انتها با زاویه \(\pi - \frac{\pi }{6}\) هستند؟ آنها را در جاهای خالی زیر مرتب کنید. آیا می توانید دو دسته زیر را از دو طرف ادامه دهید؟
\( \cdots \cdots \,,\, - 2\pi + \frac{\pi }{6}\,,\,\frac{\pi }{6}\,,\,2\pi + \frac{\pi }{6}\,,\, \cdots \cdots \) :هم انتها با \(\frac{\pi }{6}\)
\( \cdots \cdots \,,\, - \pi - \frac{\pi }{6}\,,\,\pi - \frac{\pi }{6}\,,\,3\pi - \frac{\pi }{6}\,,\, \cdots \cdots \) :هم انتها با \(\pi - \frac{\pi }{6}\)
\( - 4\pi + \frac{\pi }{6}\,,\, - 2\pi + \frac{\pi }{6}\,,\,\frac{\pi }{6}\,,\,2\pi + \frac{\pi }{6}\,,\,4\pi + \frac{\pi }{6}\) :هم انتها با \(\frac{\pi }{6}\)
\( - 3\pi - \frac{\pi }{6}\,,\, - \pi - \frac{\pi }{6}\,,\,\pi - \frac{\pi }{6}\,,\,3\pi - \frac{\pi }{6}\,,\,5\pi - \frac{\pi }{6}\) :هم انتها با \(\pi - \frac{\pi }{6}\)
بله؛ می توان دو دسته زیر را از دو طرف ادامه داد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
