1736019749.png)
جواب کار در کلاس صفحه 141 درس 8 ریاضی نهم (حجم و مساحت)
تعداد بازدید : 78.77Mپاسخ کار در کلاس صفحه 141 ریاضی نهم
-گام به گام کار در کلاس صفحه 141 درس حجم و مساحت
-کار در کلاس صفحه 141 درس 8
-شما در حال مشاهده جواب کار در کلاس صفحه 141 ریاضی نهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
1 مساحت کل هرم منتظم مقابل را به دست آورید. طول همهٔ یال های آن a است.
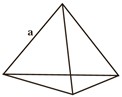
شکل گسترده هرم بدین صورت خواهد بود بنابراین داریم:
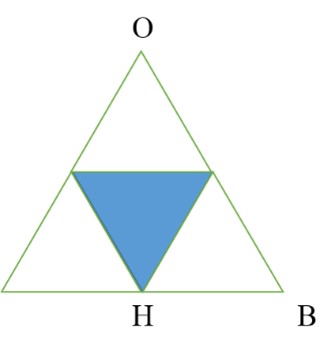
\(\begin{array}{l}O{H^2} = O{B^2} - B{H^2}\\\\ \Rightarrow {(2a)^2} - {a^2} = 4{a^2} - {a^2} = 3{a^2}\\\\ \Rightarrow OH = a\sqrt 3 \\\\ \Rightarrow S = \frac{{(a\sqrt 3 \times 2a)}}{2} = {a^2}\sqrt 3 \end{array}\)
2- با توجه به اندازه های داده شده، گستردهٔ هرم را رسم کنید و مساحت جانبی آن را به دست آورید.
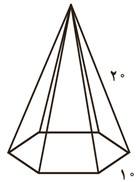
گسترده هرم به صورت زیر می شود:
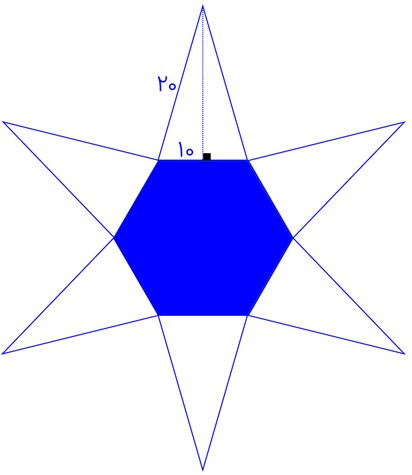
ابتدا ارتفاع یک وجه را محاسبه می کنیم:
\(\begin{array}{l}{h^2} = {20^2} - {(\frac{{10}}{2})^2} = 400 - 25 = 375\\\\ \Rightarrow h = \sqrt {375} = 5\sqrt {15} \end{array}\)
اکنون به این دلیل که همه وجه ها با یکدیگر متشابه هستند، کافی است که برای بدست آوردن مساحت جانبی هرم، مساحت یکی از وجوه را بدست آورده و در عدد 6 ضرب نماییم:
\(\begin{array}{l}{h^2} = {20^2} - {(\frac{{10}}{2})^2} = 400 - 25 = 375\\\\ \Rightarrow h = \sqrt {375} = 5\sqrt {15} \\\\S = 6 \times \frac{{5\sqrt {15} \times 10}}{2} = 150\sqrt {15} \simeq 581\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
