جواب تمرین صفحه 71 درس 3 ریاضیات گسسته (ترکیبیّات (شمارش))
تعداد بازدید : 84.72Mپاسخ تمرین صفحه 71 ریاضیات گسسته
-گام به گام تمرین صفحه 71 درس ترکیبیّات (شمارش)
-تمرین صفحه 71 درس 3
-شما در حال مشاهده جواب تمرین صفحه 71 ریاضیات گسسته هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 می خواهیم 8 نفر را که دوبه دو برادر یکدیگرند در دو طرف طول یک میز مستطیل شکل بنشانیم. اگر بخواهیم هر نفر روبه روی برادرش بنشیند، به چند طریق می توان این کار را انجام داد؟
مسئله را به این صورت بیان می کنیم که:
مطابق شکل دور یک میز 4 جفت صندلی روبروی هم داریم که می خواهیم 4 جفت برادر را روی آن ها بنشانیم. طبق اصل شمارش، این عمل به 4! حالت امکان پذیر است. از طرفی برای هر جفت صندلی که دو برادر می خواهند روی آن بنشینند، 2 حالت داریم (کدام برادر روی صندلی آبی و کدام برادر روی صندلی سبز بنشیند) و با وجود 2 صندلی طبق اصل شمارش باید 4! در 24 ضرب شود. بنابراین جواب مسئله \(4! \times {2^4}\) است.

٢ اگر داشته باشیم {A={1,2,3,4 و {B={5,6,7,8,9 در اینصورت چند رمز یا کد 5 رقمی می توان نوشت که هر یک شامل دو رقم از A و سه رقم از B باشد؟
تعداد حالات انتخاب 2 رقم از 4 رقم مجموعه ی A برابر است با: \(\left( {\begin{array}{*{20}{c}}4\\2\end{array}} \right) = 6\)
تعداد حالات انتخاب 3 رقم از 5 رقم مجموعه ی B برابر است با : \(\left( {\begin{array}{*{20}{c}}5\\3\end{array}} \right) = 10\)
از طرفی تعداد حالات چینش 5 رقم به صورت یک کد 5 رقمی برابر 5! می باشد، لذا طبق اصل ضرب جواب مسئله \(\left( {\begin{array}{*{20}{c}}4\\2\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}5\\3\end{array}} \right) \times 5! = 7200\) است.
3 4 کتاب فیزیک متفاوت و 5 کتاب ریاضی متفاوت را می توانیم به چند طریق در قفسه ای و در یک ردیف بچینیم. به نظر شما، این عمل به چند روش امکان پذیر است؟ اگر:
الف هیچ محدودیتی نباشد؛
ب همواره کتاب های فیزیک کنار هم باشند؛
پ هیچ دو کتاب ریاضی کنار هم نباشند؛
ت یک کتاب ریاضی خاص و دو کتاب فیزیک خاص همواره کنار هم باشند.
الف
چیدن 9 کتاب بدون هیچ محدودیت به 9! طریق امکان پذیر است.
ب
4 کتاب فیزیک را به عنوان یک پک کتاب که به همراه 5 کتاب ریاضی ، 6 شیء محسوب می شود و تعداد جایگشت آن ها 6! خواهد بود. از طرفی 4 کتاب فیزیک به تعداد 4! طریق با هم امکان جابجایی دارند، لذا طبق اصل ضرب، جواب مسئله \(6! \times 4!\) است.
پ
باید کتاب ها بنا به موضوع یکی در میان چیده شوند: RFRFRFRFR
لذا برای ریاضی ها 5! و برای فیزیک ها 4! حالت داریم و طبق اصل ضرب در کل \(5! \times 4!\) روش امکان پذیر است.
ت
کتاب های خاص را به عنوان یک پَک 3 تایی که به 3! طریق کنار هم قرار می گیرند، در نظر می گیریم. از طرفی یک پک به همراه 6 کتاب باقی مانده به 7! طریق می توان کنار هم چید.
در نتیجه بنا به اصل ضرب به \(3! \times 7!\) روش امکان پذیر است.
٤ برای کنار هم قرار گرفتن 4 دانش آموز پایه دوازدهم و 6 دانش آموز پایه یازدهم مسئله ای طرح کنید که پاسخ آن !4×!7 باشد.
4 دانش آموز پایه دوازدهم و 6 دانش آموز پایه یازدهم به چند طریق می توانند در یک صف کنار هم قرار بگیرند، به طوری که همواره دانش آموزان پایه دوازدهم پهلوی هم باشند؟
٥ با ارقام 5، 6، 7، 7، 5 و 7 چه تعداد کد 6 رقمی می توان نوشت؟
\(\frac{{6!}}{{2! \times 3!}}\)
٦ می خواهیم روی تعدادی جعبه حاوی اجناس تولید شده خاصی را کدگذاری و هر جعبه را با یک کد، شامل 9 حرف d,d,d,c,c,a,b,a,a از بقیه مجزا کنیم. حداکثر چند جعبه را می توانیم با این کدها از بقیه مجزا کنیم؟
\(\frac{{9!}}{{3! \times 3! \times 2!}}\)
7 7 نفر به چند طریق می توانند در دو اتاق دونفره و یک اتاق سه نفره قرار بگیرند؟
\(\frac{{7!}}{{3! \times 2! \times 2!}}\)
٨ به چند طریق می توان از بین 5 نوع گل 11 شاخه گل انتخاب کرد اگر بخواهیم:
الف به دلخواه انتخاب کنیم؛
ب از هر نوع گل حداقل 1 شاخه انتخاب کنیم؛
پ از گل نوع دوم حداقل دو شاخه و از گل نوع پنجم بیش از سه شاخه انتخاب کنیم؛
ت از گل نوع سوم انتخاب نکرده و از گل نوع چهارم حداقل 5 شاخه انتخاب کنیم.
الف
\({x_i}\) را به عنوان گُل نوع \(i\)اُم معرفی می کنیم، در نتیجه جواب مسئله همان تعداد جواب های صحیح نامنفی معادله \({x_1} + {x_2} + {x_3} + {x_4} + {x_5} = 11\) است. بنابراین پاسخ آن \(\left( {\begin{array}{*{20}{c}}{11 + 5 - 1}\\{5 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{15}\\4\end{array}} \right)\) است.
ب
تعداد جواب های صحیح مثبت معادله قسمت قبل، جواب مسئله می باشد: \(\left( {\begin{array}{*{20}{c}}{11 - 1}\\{5 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{10}\\4\end{array}} \right)\)
پ
یعنی در معادله \({x_1} + {x_2} + {x_3} + {x_4} + {x_5} = 11\) شرایط \({x_2} \ge 2\) و \({x_5} > 3\) به همراه صحیح و نامنفی بودن دیگر متغیرهای آن برقرار است:
\(\begin{array}{l}\left. \begin{array}{l}{x_2} \ge 2 \Rightarrow \underbrace {{x_2} - 2}_{{y_2}} \ge 0\\{x_5} > 3 \Rightarrow {x_5} \ge 4\end{array} \right\} \Rightarrow \\\\\left. \begin{array}{l}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{x_2} = {y_2} + 2\\\underbrace {{x_5} - 4}_{{y_5}} \ge 0 \Rightarrow {x_5} = {y_5} + 4\end{array} \right\} \Rightarrow \\\\{x_1} + {y_2} + 2 + {x_3} + {x_4} + {y_5} + 4 = 11\\\\ \Rightarrow {x_1} + {y_2} + {x_3} + {x_4} + {y_5} = 5\\\\ \Rightarrow \left( {\begin{array}{*{20}{c}}{5 + 5 - 1}\\{5 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}9\\4\end{array}} \right)\end{array}\)
ت
یعنی در معادله \({x_1} + {x_2} + {x_3} + {x_4} + {x_5} = 11\) شرایط \({x_3} = 0\) و \({x_4} \ge 5\) به همراه صحیح و نامنفی بودن دیگر متغیرهای آن برقرار است:
\(\begin{array}{l}{x_4} \ge 5 \Rightarrow \underbrace {{x_4} - 5}_{{y_4}} \ge 0 \Rightarrow {x_4} = {y_4} + 5\;\\\\\;\mathop \Rightarrow \limits^{{x_3} = 0} \;\;{x_1} + {x_2} + 0 + {y_4} + 5 + {x_5} = 11\\\\ \Rightarrow {x_1} + {x_2} + {y_4} + {x_5} = 6\\\\ \Rightarrow \left( {\begin{array}{*{20}{c}}{6 + 4 - 1}\\{4 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}9\\3\end{array}} \right)\end{array}\)
٩ مطلوب است تعداد جواب های صحیح و نامنفی هریک از معادلات زیر با شرط های داده شده:
الف \({x_1} + {x_2} + ... + {x_5} = 10\;\;\;\;{x_i} > 0\;,\;2 \le i \le 5\)
ب \({x_1} + {x_2} + ... + {x_6} = 12\;\;\;\;{x_1} > 2\;,\;{x_5} \ge 4\)
پ \({x_1} + {x_2} + ... + {x_5} = 11\;\;\;\;{x_i} \ge 1\;,\;1 \le i \le 5\)
ت \({x_1} + 3{x_2} + {x_3} + {x_4} = 7\;\;\;\;{x_i} \ge 0\;,\;1 \le i \le 4\)
ث \({x_1} + \sqrt {{x_2}} + {x_3} + {x_4} = 3\;\;\;\;{x_i} \ge 0\;,\;1 \le i \le 4\)
الف
\(\begin{array}{l}\mathop \Rightarrow \limits^{2 \le i \le 5} \;\;{x_i} > 0 \Rightarrow {x_i} \ge 1\\\\ \Rightarrow \underbrace {{x_i} - 1}_{{y_i}} \ge 0 \Rightarrow {x_i} = {y_i} + 1\\\\ \Rightarrow {x_1} + {y_2} + 1 + {y_3} + 1 + {y_4} + 1 + {y_5} + 1 = 10\\\\ \Rightarrow {x_1} + {y_2} + {y_3} + {y_4} + {y_5} = 6\\\\ \Rightarrow \left( {\begin{array}{*{20}{c}}{6 + 5 - 1}\\{5 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{10}\\4\end{array}} \right)\end{array}\)
ب
\(\begin{array}{l}\left. \begin{array}{l}{x_1} > 2 \Rightarrow {x_1} \ge 3 \Rightarrow \underbrace {{x_1} - 3}_{{y_1}} \ge 0 \Rightarrow {x_1} = {y_1} + 3\\{x_5} \ge 4 \Rightarrow \underbrace {{x_5} - 4}_{{y_5}} \ge 0 \Rightarrow {x_5} = {y_5} + 4\end{array} \right\}\\\\ \Rightarrow {y_1} + 3 + {x_2} + {x_3} + {x_4} + {y_5} + 4 + {x_6} = 12\\\\ \Rightarrow {y_1} + {x_2} + {x_3} + {x_4} + {y_5} + {x_6} = 5\\\\ \Rightarrow \left( {\begin{array}{*{20}{c}}{5 + 6 - 1}\\{6 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{10}\\5\end{array}} \right)\end{array}\)
پ
طبق شرط مسئله، باید تعداد جواب های صحیح و مثبت (طبیعی) را حساب کنیم که برابر است با:
\(\left( {\begin{array}{*{20}{c}}{11 - 1}\\{5 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{10}\\4\end{array}} \right)\)
ت
بدیهی است که با توجه به ضریب x2 ، برای آن 3 حالت می توان در نظر گرفت:
\({x_2} = 0 \Rightarrow {x_1} + {x_3} + {x_4} = 7 \Rightarrow \) :حالت اول
\(\left( {\begin{array}{*{20}{c}}{7 + 3 - 1}\\{3 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}9\\2\end{array}} \right) = 36\) :تعداد جواب های صحیح نامنفی
\({x_2} = 1 \Rightarrow {x_1} + {x_3} + {x_4} = 4 \Rightarrow \) :حالت دوم
\(\left( {\begin{array}{*{20}{c}}{4 + 3 - 1}\\{3 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}6\\2\end{array}} \right) = 15\) :تعداد جواب های صحیح نامنفی
\({x_2} = 2 \Rightarrow {x_1} + {x_3} + {x_4} = 1 \Rightarrow \) :حالت سوم
\(\left( {\begin{array}{*{20}{c}}{1 + 3 - 1}\\{3 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}3\\2\end{array}} \right) = 3\) :تعداد جواب های صحیح نامنفی
\(36 + 15 + 3 = 54\) :مجموع حالت ها
ث
با توجه به شرایط معادله، چهار حالت برای x2 وجود دارد:
\({x_2} = 0 \Rightarrow {x_1} + {x_3} + {x_4} = 3 \Rightarrow \) :حالت اول
\(\left( {\begin{array}{*{20}{c}}{3 + 3 - 1}\\{3 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}5\\2\end{array}} \right) = 10\) :تعداد جواب های صحیح نامنفی
\({x_2} = 1 \Rightarrow {x_1} + {x_3} + {x_4} = 2 \Rightarrow \) :حالت دوم
\(\left( {\begin{array}{*{20}{c}}{2 + 3 - 1}\\{3 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}4\\2\end{array}} \right) = 6\) :تعداد جواب های صحیح نامنفی
\({x_2} = 4 \Rightarrow {x_1} + {x_3} + {x_4} = 1 \Rightarrow \) :حالت سوم
\(\left( {\begin{array}{*{20}{c}}{1 + 3 - 1}\\{3 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}3\\2\end{array}} \right) = 3\) :تعداد جواب های صحیح نامنفی
\({x_2} = 9 \Rightarrow {x_1} + {x_3} + {x_4} = 0 \Rightarrow \) :حالت چهارم
\( = \left( {\begin{array}{*{20}{c}}{0 + 3 - 1}\\{3 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}2\\2\end{array}} \right) = 1\) :تعداد جواب های صحیح نامنفی
\(10 + 6 + 3 + 1 = 20\) :مجموع حالت ها
10 به چند طریق می توان 5 توپ یکسان را بین 3 نفر و به دلخواه توزیع کرد؟
\( = \left( {\begin{array}{*{20}{c}}{5 + 3 - 1}\\{3 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}7\\2\end{array}} \right) = 21\) تعداد جواب های صحیح نامنفی \({x_1} + {x_2} + {x_3} = 5\mathop \to \limits^{{x_i} \ge \;0} \)
به 21 طریق می توان 5 توپ یکسان را بین 3 نفر توزیع کرد.
11 به چند طریق می توان 8 توپ یکسان را بین 4 نفر توزیع کرد هرگاه بخواهیم هر نفر حداقل یک توپ داشته باشد؟
\({x_1} + {x_2} + {x_3} + {x_4} = 8\mathop \to \limits^{{x_i} \ge \;1} \)
\(\left( {\begin{array}{*{20}{c}}{8 - 1}\\{4 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}7\\3\end{array}} \right) = 35\) :تعداد جواب های صحیح و مثبت (طبیعی)
به 35 طریق می توان 8 توپ یکسان را بین 4 نفر چنان توزیع کرد که به هر نفر حداقل یک توپ تعلق گیرد.
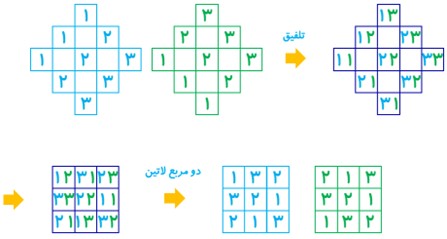
12 آیا مربع لاتین حاصل از اعمال یک جایگشت روی اعضای یک مربع لاتین دلخواه می تواند با مربع اولیه متعامد باشد؟
خیر، امکان ندارد متعامد باشند؛ زیرا اگر مثلا در جایگشت، \(1 \to a\) باشد، آن گاه در مقابل تمام 1 های مربع اول، عدد \(a\) در مربع دوم ظاهر می شود که در مربع تلفیق زوجِ \(1a\) تکراری خواهد بود. برای درک بهتر به مربع روبرو همراه با جایگشت آن دقت کنید:

13 مربع لاتین 3 × 3 مقابل را در نظر بگیرید.
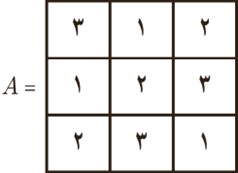
الف سطر دوم و سوم مربع A را جابه جا کنید و مربع حاصل را A1 بنامید. آیا A و A1 متعامدند؟
ب ابتدا سطر اول و سطر سوم مربع A را جابه جا کنید. سپس در مربع حاصل، سطر دوم و سوم را جابه جا کنید و مربع حاصل را A2 بنامید. آیا A و A2 متعامدند؟
پ با توجه به قسمت های (الف) و (ب) به سؤالات زیر جواب دهید.
1 آیا می توان گفت با تعویض جای سطرهای یک مربع لاتین، همواره مربع لاتینی متعامد با مربع لاتین اول به دست می آید؟
2 آیا می توان گفت با تعویض جای سطرهای یک مربع لاتین، همواره مربع لاتینی غیرمتعامد با مربع لاتین اول به دست می آید؟
الف

متعامد هستند.
ب

همانطور که مشاهده می کنیم متعامد نیستند.
پ
1
خیر؛ به طور قطع نمی توان گفت، ممکن است متعامد باشند یا نباشند.
2
خیر؛ در بعضی مواقع ممکن است.
14 قرار است شش مدرس T1 ، T2 و ... و T6 در شش جلسه متوالی در شش کلاس C1 ، C2 و ... و C6 به گونه ای تدریس کنند که هر مدرس در هر کلاس دقیقا یک جلسه تدریس کند. برای این منظور برنامه ریزی نمایید.
یک مربع لاتین \(6 \times 6\) که هر سطر آن یکی از جلسات و هر ستون آن یکی از کلاس ها را مشخص می کند. به عنوان نمونه معلم T1 جلسه اول را در کلاس C1 است.

15 دو مربع لاتین متعامد از مرتبه 3 و دو مربع لاتین متعامد از مرتبه 7 بنویسید.



16 در یک مسابقه اتومبیل رانی قرار است 7 راننده در هفت روز هفته با هفت ماشین مختلف در هفت مسیر مختلف مسابقه دهند به طوریکه شرایط زیر برقرار باشد:
الف هر راننده هر روز با یک ماشین در یک مسیر رانندگی کند؛
ب هر راننده با هر ماشین دقیقا یک روز رانندگی کند؛
پ هر راننده هر روز دقیقا در یک مسیر رانندگی کند؛
ت هر ماشین در هر مسیر دقیقایکبار به کار گرفته شود.
ــ برای این منظور یک برنامه ریزی انجام دهید.
کافی است دو مربع لاتین 7×7 بنویسیم به طوری که سطرهای آن ها، روزهای هفته و ستون های آن ها، راننده ها نام گذاری شوند. برای سهولت در نوشتن، راننده ها را \(a\;,\;b\;,\;c\;,\;d\;,\;e\;,\;f\;,\;g\) نام گذاری می کنیم.
اگر آن دو مربع را A و B بنامیم، اعداد درون مربع های A شماره ماشین و اعداد درون مربع های B شماره مسیر را مشخص می کنند. لذا مربع حاصل از کنار هم قرر دادن درایه های آن ها، جواب مسئله است.
برای این منظور از مربع های بدست آمده در سوال 15 استفاده می کنیم:

مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















