جواب تمرین صفحه 41 درس 2 ریاضیات گسسته (گراف و مدل سازی)
تعداد بازدید : 84.72Mپاسخ تمرین صفحه 41 ریاضیات گسسته
-گام به گام تمرین صفحه 41 درس گراف و مدل سازی
-تمرین صفحه 41 درس 2
-شما در حال مشاهده جواب تمرین صفحه 41 ریاضیات گسسته هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 گراف G با مجموعه رأس های {V(G) = {a, b, c, d, e, f و مجموعه یال های {E(G)={ab, ac, cd, ef, db, cf, be مفروض است. نمودار آن را رسم کنید و به موارد زیر جواب دهید.
الف مرتبه و اندازه گراف G را بنویسید.
ب درجه رأس های G را مشخص نمایید.
پ مجموع درجات رئوس این گراف برابر چند است؟
ت کدام رأس های گراف G با رأس f مجاورند؟
ث گراف H با مجموعه رأس های {V(H) = {v1 , v2 , v3 , v4
و مجموعه یال های {E(H)={v1v2,v1v3,v2v3,v2v4,v3v4,v4v1 مفروض است. بدون کشیدن نمودار آن به قسمت های (الف) تا (پ) در مورد گراف H پاسخ دهید.
الف
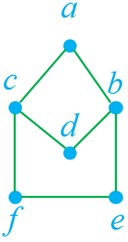
p = 6 , q = 7
ب
\(\begin{array}{l}\deg (a) = \deg (d) = \deg (e) = \deg (f) = 2\;\;,\\\\\deg (b) = \deg (c) = 3\end{array}\)
پ
c و e
ت
\(2 + 3 + 2 + 2 + 3 + 2 = 14\)
ث
الف) q = 6 و p = 4
ب) \(\deg ({v_1}) = \deg ({v_2}) = \deg ({v_3}) = \deg ({v_4}) = 3\)
پ) رأس f در این گراف تعریف نشده است.
ت) 12 = 3 × 4
٢ گراف G (شکل 21) را در نظر بگیرید.
الف مجموعه های (V(G و (E(G را بنویسید.
ب \(Δ(G)\) و \(δ(G)\) را مشخص نمایید.
پ مجموعه همسایه های رأس های f و g و e را بنویسید.
ت اگر {NG(x) = {a , c آنگاه x کدام رأس است؟
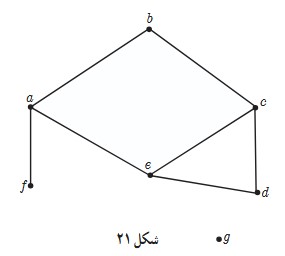
الف
\(\begin{array}{l}V(G) = \left\{ {a\;,\;b\;,\;c\;,\;d\;,\;e\;,\;f\;,\;g} \right\}\\\\E(G) = \left\{ {ab\;,\;ae\;,\;af\;,\;bc\;,\;cd\;,\;ce\;,\;de} \right\}\end{array}\)
ب
\(\Delta (G) = 3\quad ,\quad \delta (G) = 0\)
پ
\(\begin{array}{l}{N_G}(f) = \left\{ a \right\}\\\\{N_G}(g) = \emptyset \\\\{N_G}(e) = \left\{ {a\;,\;c\;,\;d} \right\}\end{array}\)
ت
x رأسی هست که هم با a و هم با c همسایه باشد، با توجه به شکل، x=b است.
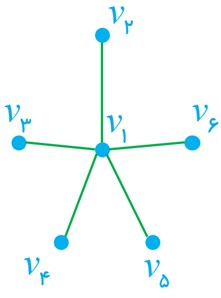
3 گراف G با مجموعه رأس های {V(G) = {v1 , v2 , v3 , v4 , v5 , v6 مفروض است. اگر (NG(v1 دارای 5 عضو باشد و مجموعه های (NG(vi برای 2 ≤ i ≤ 6 تک عضوی باشند، گراف G را رسم کنید.
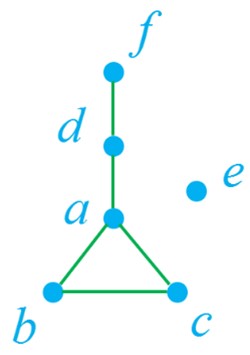
4 در گراف G با مجموعه رأس های {V(G) = {a , b , c , d , e , f داریم:
\(\begin{array}{*{20}{l}}{{N_G}\left( a \right){\rm{ }} = {\rm{ }}\left\{ {b{\rm{ }},{\rm{ }}c{\rm{ }},{\rm{ }}d} \right\}}\\{{N_G}\left( b \right){\rm{ }} = {\rm{ }}\left\{ {a{\rm{ }},{\rm{ }}c} \right\}}\\{{N_G}\left( c \right){\rm{ }} = {\rm{ }}\left\{ {a{\rm{ }},{\rm{ }}b} \right\}}\\{{N_G}\left( d \right){\rm{ }} = {\rm{ }}\left\{ {a{\rm{ }},{\rm{ }}f} \right\}}\\{{N_G}\left( e \right){\rm{ }} = {\rm{ }}\left\{ \; \right\}}\\{{N_G}\left( {f{\rm{ }}} \right){\rm{ }} = {\rm{ }}\left\{ d \right\}}\end{array}\)
گراف G را رسم و اندازه آن را مشخص کنید.
٥ گراف G (شکل 22) رسم شده است. مجموع درجه های رأس های گراف G را مشخص کنید و همچنین درجات رئوس a و c در گراف G را تعیین نمایید.
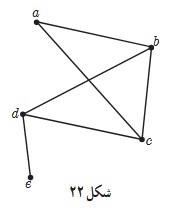
تعداد یال های گراف\( - \;G\) تعداد کل یال های ممکن در گراف 5 رأسی \( = \;({K_5})\) تعداد یال های گراف \(\overline G \)
\(\; = \;8\) مجموع درجات گراف \( = \frac{{5 \times 4}}{2} - 6 = 4\overline G \)تعداد یال های گراف \( \Rightarrow \quad \overline G \)
\(\quad \Rightarrow \quad \left\{ \begin{array}{l}{\deg _G}(a) = 2 \Rightarrow {\deg _{\overline G }}(a) = 4 - 2 = 2\\{\deg _G}(c) = 3 \Rightarrow {\deg _{\overline G }}(c) = 4 - 3 = 1\end{array} \right.\) درجه هر رأس در گراف کامل 4 است.
٦ گراف کامل Kp دارای 36 یال است. در این گراف \(Δ(G)\) و \(δ(G)\) را مشخص کنید.
در گراف کامل p رأسی تعداد یال ها برابر است با\(\frac{{p(p - 1)}}{2}\) ؛ در نتیجه:
\(\frac{{p(p - 1)}}{2} = 36 \Rightarrow p(p - 1) = 72 \Rightarrow p = 9\)
از طرفی گراف کامل\({K_9}\) یک گراف 8 – منتظم است؛ بنابراین درجه تمام رئوس یکسان بوده و\(\Delta = \delta = 8\) است.
٧ گراف های کامل از مرتبه 1 تا 5 را رسم کنید.
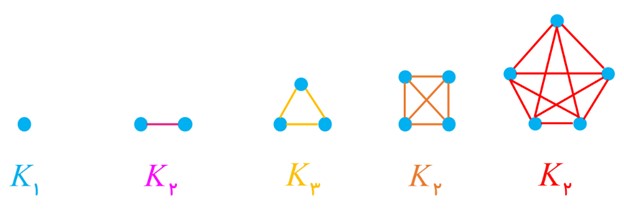
٨ در هر یک از حالات زیر در صورت امکان یک گراف -r منتظم از مرتبه n رسم کنید.
الف n=4 r=1
ب n=4 r=2
پ n=5 r=2
ت n=5 r=3
ث n=6 r=4
ج n=7 r=3
الف
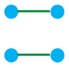
ب
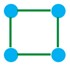
پ
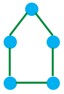
ت
امکان پذیر نیست؛ زیرا مجموع در حالت 15=5×3، عدد فرد بوده و طبق قضیه بایستی زوج باشد.
ث
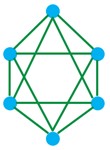
ج
امکان پذیر نیست؛ زیرا مجموع در حالت 21=7×3، عدد فرد بوده و طبق قضیه بایستی زوج باشد.
٩ برای هر یک از حالت های زیر در صورت امکان یک گراف 5 رأسی رسم کنید به طوریکه:
الف یک رأس تنها داشته باشد.
ب دو رأس تنها داشته باشد.
پ سه رأس تنها داشته باشد.
ت چهار رأس تنها داشته باشد.
ث پنج رأس تنها داشته باشد.
الف
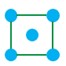
ب
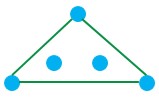
پ
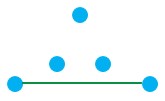
ت
امکان پذیر نیست؛ زیرا اگر بخواهیم چهار رأس تنها باشند، رأس پنجم نمی تواند به هیچ کدام از آن ها متصل شود، پس رأس پنجم نیز تنها خواهد ماند!
ث

10 هفت نفر در یک اتاق هستند و برخی از آنها با یکدیگر دست می دهد. 6 نفر از آنها هر کدام دقیقا با 2 نفر دست داده اند. نشان دهید نفر هفتم نمی تواند دقیقا با 5 نفر دست داده باشد.
اگر هفت نفر به عناون 7 رأس یک گراف در نظر بگیریم و در صورتی که دو نفر با هم دست بدهند، بین دو رأس منسوب به آن ها یال رسم مس کنیم. در نتیجه 6 رأس گراف درجه 2 خواهد بود و اگر رأس هفتم درجه 5 باشد، یعنی پراف دارای یک رأس درجه فرد است که با نتیجه ی قضیه تناقض دارد، زیرا باید تعداد رئوس درجه فرد، زوج باشد، پس نفر هفتم نمی تواند با 5 نفر دست داده باشد.
11 علی، سامان، محمد، ناصر و مهرداد، در یک شبکه اجتماعی عضو هستند و هر کدام از آنها ممکن است در فهرست دوستان هر کدام از 4 نفر دیگر باشد یا نباشد.
الف چند حالت مختلف می تواند وجود داشته باشد؟
ب اگر بودن در فهرست دوستان به این صورت باشد که هر دونفر، یا هر دو در فهرست دوستان هم هستند و یا هیچکدام در فهرست دوستان دیگری نیست، در این صورت چند حالت مختلف می تواند وجود داشته باشد؟
الف
5 نفر را به عنوان 5 رأس یک گراف جهت دارد در نظر می گیریم. به طور مثال اگر نام علی در فهرست دوستان سامان وجود دارد، یک یال جهت دار از علی به سمت سامان رسم می کنیم و برعکس، اگر نام سامان در فهرست دوستان علی باشد، یک یال جهت دار از سامان به علی رسم می کنیم. به همین ترتیب الی آخر پیش می رویم.
حداکثر تعداد یال ها در گراف جهت دار 5 رأسی\(p(p - 1) = 5 \times 4 = 20\) می باشد.
از طرفی برای هر یال دو حالت داریم ( وجود داشتن یا وجود نداشتن آن یال)؛ پس تعداد کل حالات برای آن\({2^{20}}\) می باشد.
ب
این قسمت همچون قسمت الف بوده، با این تفاوت که گراف جهت دار نیست. پس حداکثر تعداد یال ها\(\frac{{p(p - 1)}}{2} = \frac{{5 \times 4}}{2} = 10\) می باشد. بنابراین تعداد کل حالات 210 می باشد.
1٢ یک گراف 9 رأسی رسم کنید به طوریکه:
الف دورهایی به طول 5 و 6 و 7 و 9 داشته باشد و هیچ دوری به طول غیر از اعداد مذکور نداشته باشد.
ب دورهایی به طول 5 و 6 و 8 و 9 داشته باشد و دوری به طول غیر از اعداد مذکور نداشته باشد.
الف
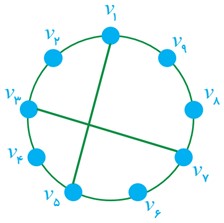
\({v_1}{v_2}{v_3}{v_4}{v_5}{v_1}\) :دوری به طول 5
\({v_1}{v_5}{v_6}{v_7}{v_8}{v_9}{v_1}\) :دوری به طول 6
\({v_1}{v_5}{v_4}{v_3}{v_7}{v_8}{v_9}{v_1}\) :دوری به طول 7
\({v_1}{v_5}{v_6}{v_7}{v_8}{v_9}{v_1}\) :دوری به طول 9
ب
ابتدا همچون قسمت الف با دوری به طول 9 رسم می کنیم و از\({v_1}\) به\({v_5}\) یالی رسم کرده تا دورهایی به طول 6 و 5 ساخته شود.
حال برای ساختن دورهایی به طول های 7 و 8 باید یال دیگری رسم کنیم. به طور مثال رأس\({v_2}\) را انتخاب می کنیم که فقط می توان آن را به رأس\({v_7}\) رسم کرد؛ زیرا در غیر این صورت دورهایی به طول 3 یا 4 ایجاد می شود که خواست مسئله نیست.
اگر مطابق شکل (یال آبی رنگ)\({v_2}\) را به\({v_7}\) وصل کنیم دور به طول 8 ایجاد می شود (\({v_2}{v_3}{v_4}{v_5}{v_1}{v_9}{v_8}{v_7}{v_2}\)) ولی دور به طول 7 ایجاد نمی شود!
همچنین در قسمت قبل مشاهده شد که اگر رأس\({v_3}\) انتخاب شود، دور به طول 7 ایجاد شده ولی به طول 8 ایجاد نمی شود!
به همین ترتیب با انتخاب رئوس دیگر متوجه می شویم که با این کار با رسم دو قطر امکان پذیر نیست.
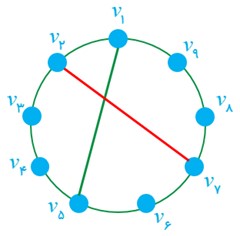
اما در صورتی که سه قطر رسم کنیم، یکی برای ایجاد دورهایی به طول 5 و 6 و دیگری برای به طول 7 و سومی برای ایجاد دور به طول 8، باز هم قابل قبول نبوده؛ زیرا دورهایی به طول 3 یا 4 نیز ساخته شده که خواسته مسئله نیست. بنابراین چنین گرافی وجود ندارد.
13 فرض کنید G یک گراف باشد و \(δ(G) ≥ K\) درستی یا نادرستی هر یک از موارد زیر را ثابت کنید.
الف G لزوما شامل یک مسیر به طول K است.
ب G لزوما شامل یک مسیر به طول K + 1 است.
الف
درست است؛ اثبات:
رأس دلخواه\({v_1}\) را در گراف\(G\) در نظر می کیریم، حتما\({v_1}\) به رأس دیگری ( مثل\({v_2}\) ) متصل است؛ زیرا در غیر این صورت\(\delta = 0\) خواهد شد. همچنین \({v_2}\) به رأسی به جز\({v_1}\) متصل می باشد ( مثل\({v_3}\) ) زیرا در غیر این صورت\(\delta = 1\) خواهد شد.
حتما\({v_3}\) به رأسی به غیر از\({v_1}\) و\({v_2}\) ( مثل\({v_4}\) ) وصل است؛ زیرا در غیر این صورت، حداکثر مقدار \(\delta \)، دو خواهد بود. این روند ادامه دارد تا به رأس جدید\({v_k}\) برسیم که با استدلال مشابه قبل بایستی به رأس جدیدی مانند\({v_{K + 1}}\) وصل باشد. بنابراین مسیر\({v_1}{v_2}{v_3} \cdots {v_{K + 1}}\) یک مسیر به طول\(K\) در گراف\(G\) است.
ب
نادرست است. مثال نقض برای ردّ آن مطرح می کنیم:
مثال نقض اول: در گراف یک رأسی روبرو\(K = \delta = 0\) مسیری به طول\(0 + 1 = 1\) وجود ندارد.

مثال نقض دوم: در گراف دو رأسی روبرو\(K = \delta = 1\) مسیری به طول\(1 + 1 = 2\) وجو ندارد.

توجه : هر گراف کامل می تواند یک مثال نقض برای آن محسوب شود.
14 یک گراف 4 رأسی غیر تهی -K منتظم بکشید که:
الف K بیشترین مقدار ممکن را داشته باشد.
ب K کمترین مقدار ممکن را داشته باشد.
الف

ب
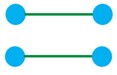
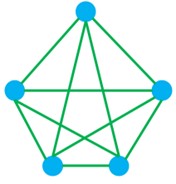
1٥ یک گراف 5 رأسی غیر تهی -K منتظم بکشید که:
الف K بیشترین مقدار ممکن را داشته باشد.
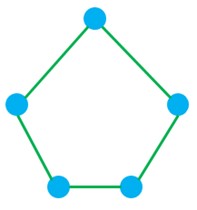
ب K کمترین مقدار ممکن را داشته باشد.
الف
ب
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















