آیا تمام سوالات کار در کلاس صفحه 46 ریاضیات گسسته، مطابق با آخرین تغییرات کتب درسی پاسخ داده شده است ؟

بله، تمام جواب ها به کار در کلاس صفحه 46 ریاضیات گسسته مطابق با آخرین تغییرات کتب درسی 1402 - 1401 است.

آیا جواب ها به صورت آموزش محور و کامل بیان شده اند ؟

بله، جواب سوالات به صورت کاملا تشریحی و با هدف یادگیری و تسلط به مبحث بیان شده اند.

جواب کار در کلاس صفحه 46 درس 2 ریاضیات گسسته (گراف و مدل سازی)

تعداد بازدید : 78.8M

پاسخ کار در کلاس صفحه 46 ریاضیات گسسته

گام به گام کار در کلاس صفحه 46 درس گراف و مدل سازی

کار در کلاس صفحه 46 درس 2

شما در حال مشاهده جواب کار در کلاس صفحه 46 ریاضیات گسسته هستید. ما در تیم مای درس، پاسخ‌نامه‌های کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کرده‌ایم. اگر به دنبال به‌روزترین پاسخ‌ها برای این صفحه هستید و می‌خواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخ‌های گام به گام، به گنجینه‌ای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مای‌درس را نصب نمایید.

1 مشخص کنید کدام یک ازمجموعه های زیر برای گراف شکل 5 احاطه گر هست و کدام نیست؟

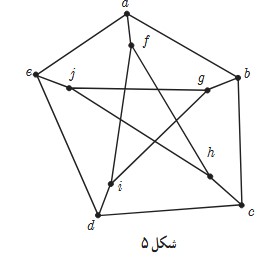
الف A = {a, b, c, d, e}

ب B = {f, g, h, I, j}

پ C = {a, b, j, h, g}

ت D = {a, I, h}

ث E = {f, g, h, e, d}

ج F = {f, g, h, e}

چ H = {g, h, e}

الف

احاطه گر هست

احاطه گر نیست

احاطه گر هست

٢ از مجموعه های مطرح شده در سؤال 1 که احاطه گر بودند در کدام یک از آنها رأس یا رأس هایی وجود دارد که با حذف آنها مجموعه باقیمانده هنوز احاطه گر باشد؟

تعریف: یک مجموعه احاطه گر را که با حذف هر یک از رأس هایش دیگر احاطه گر نباشد احاطه گر مینیمال می نامیم.

قسمت ت؛ اگر از مجموعه ی\(E = \left\{ {f\;,\;g\;,\;h\;,\;e\;,\;d} \right\}\) رأس\(d\) را حذف کنیم، مجموعه جدید همان مجموعه\(F = \left\{ {f\;,\;g\;,\;h\;,\;e} \right\}\) بوده که احاطه گر است.

3 مجموعه ای احاطه گر با کمترین تعداد رأس که می توانید، بنویسید و پاسخ خود را با پاسخ هم کلاسی های خود مقایسه کنید.

\(F = \left\{ {c\;,\;j\;,\;f} \right\}\)

4 یک مجموعه احاطه گر مینیمال مشخص کنید که مینیمم نباشد.

\(A = \left\{ {a\;,\;b\;,\;c\;,\;d\;,\;e} \right\}\)

5 آیا می توان هر مجموعه احاطه گر دلخواه غیرمینیمال را با حذف برخی رئوسش به یک مجموعه احاطه گر مینیمال تبدیل کرد؟ (استدلال کنید)

بله؛ اگر\(A = \left\{ {{v_1}\;,\;{v_2}\;,\; \cdots \;,\;{v_n}} \right\}\) یک مجموعه احاطه گر باشد، عضوی مانند v₁ را در نظر می کیریم، اگر با حذف آن، هنوز مجموعه احاطه گر باقی ماند، آن را حذف می کنیم، در غیر این صورت آن را نگه داشته و همین کار را برای سایر رئوس انجام می دهیم. با توجه به غیر مینیمال بودنِ مجموعه، قطعاً حداقل یک عضو یافت می شود که با حذف آن، هنوز احاطه گر خواهد ماند.