جواب تمرین صفحه 83 درس 3 ریاضیات گسسته (ترکیبیّات (شمارش))
تعداد بازدید : 86.34Mپاسخ تمرین صفحه 83 ریاضیات گسسته
-گام به گام تمرین صفحه 83 درس ترکیبیّات (شمارش)
-تمرین صفحه 83 درس 3
-شما در حال مشاهده جواب تمرین صفحه 83 ریاضیات گسسته هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 در بین اعداد طبیعی 1 تا 90 (\(1≤n≤90\)) چند عدد وجود دارد که بر 2 یا 3 بخش پذیر باشند؟
مجموعه اعدادی که بر 2 بخش پذیرند را با A و مجموعه اعدادی که بر 3 بخش پذیرند را با B نمایش می دهیم. بنابراین:
\(\begin{array}{l}\left. \begin{array}{l}\left| A \right| = \left[ {\frac{{90}}{2}} \right] = 45\\\left| B \right| = \left[ {\frac{{90}}{3}} \right] = 30\\\left| {A \cap B} \right| = \left[ {\frac{{90}}{6}} \right] = 15\end{array} \right\}\\\\\\ \Rightarrow \left| {A \cup B} \right| = \left| A \right| + \left| B \right| - \left| {A \cap B} \right|\\\\ = 45 + 30 - 15 = 60\end{array}\)
٢ در بین اعداد طبیعی 1 تا 200(1≤n≤200) چند عدد وجود دارد که بر 4 بخش پذیر باشند ولی بر 7 بخش پذیر نباشند؟
مجموعه اعدادی که بر 4 بخش پذیرند را با A و مجموعه اعدادی که بر 7 بخش پذیرند را با B نمایش می دهیم. بنابراین:
\(\begin{array}{l}\left. \begin{array}{l}\left| A \right| = \left[ {\frac{{200}}{4}} \right] = 50\\\left| {A \cap B} \right| = \left[ {\frac{{200}}{{28}}} \right] = 7\end{array} \right\}\\\\ \Rightarrow \left| {A - B} \right| = \left| {A \cap B'} \right| = \left| A \right| - \left| {A \cap B} \right|\\\\ = 50 - 7 = 43\end{array}\)
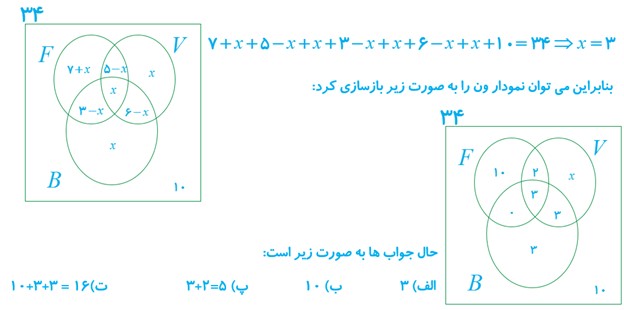
٣ در یک کلاس 34 نفری، 15 نفر فوتبال بازی می کنند، 11 نفر والیبال و 9 نفر بسکتبال بازی می کنند. اگر بدانیم 10 نفر عضو هیچ یک از این سه تیم نبوده و 5 نفر فوتبال و والیبال، 6 نفر والیبال و بسکتبال و 3 نفر فوتبال و بسکتبال بازی می کنند مشخص کنید:
الف چند نفر هر سه رشته ورزشی را بازی می کنند؟
ب چند نفر فقط فوتبال بازی می کنند؟
پ چند نفر والیبال بازی می کنند ولی بسکتبال بازی نمی کنند؟
ت چند نفر فقط در یک رشته بازی می کنند؟
الف
\(\begin{array}{l}\left\{ \begin{array}{l}\left| F \right| = 15\\\left| V \right| = 11\\\left| B \right| = 9\end{array} \right.\;\;\;,\;\;\;\left\{ \begin{array}{l}\left| {V \cap B} \right| = 5\\\left| {F \cap B} \right| = 3\\\left| {F \cap V} \right| = 5\end{array} \right.\;\;,\\\\\left| {F \cup V \cup B} \right| = 34 - 10 = 24\\\\\left| {F \cup V \cup B} \right| = \left| F \right| + \left| V \right| + \left| B \right| - \left| {F \cap V} \right| - \left| {V \cap B} \right| - \left| {F \cap B} \right| + \left| {F \cap V \cap B} \right|\\\\ \Rightarrow 24 = 15 + 11 + 9 - 5 - 6 - 2 + \left| {F \cap V \cap B} \right| \Rightarrow \left| {F \cap V \cap B} \right| = 2\end{array}\)
ب
\(\left| F \right| - \left| {F \cap V} \right| - \left| {F \cap B} \right| + \left| {F \cap V \cap B} \right| = 15 - 5 - 3 + 3 = 10\)
پ
\(\left| {V - B} \right| = \left| V \right| - \left| {V \cap B} \right| = 11 - 6 = 5\)
ت
\( = \left| F \right| - \left| {F \cap V} \right| - \left| {F \cap B} \right| + \left| {F \cap V \cap B} \right| = 15 - 5 - 3 + 3 = 10\) فقط فوتبال
\( = \left| V \right| - \left| {F \cap V} \right| - \left| {V \cap B} \right| + \left| {F \cap V \cap B} \right| = 11 - 5 - 6 + 3 = 3\) فقط والیبال
\( = \left| B \right| - \left| {B \cap F} \right| - \left| {V \cap B} \right| + \left| {F \cap V \cap B} \right| = 9 - 3 - 6 + 3 = 3\) فقط بسکتبال
16 = فقط بسکتبال + فقط والیبال + فقط فوتبال
روش ساده تر:
پیشنهاد می شود برای حل این نوع سوالات از نمودار ون به شکل زیر استفاده شود:
٤ اگر بخواهیم یک قفل دارای رمز 5 رقمی و فاقد صفر را که سه رقم آن 7 و 2 و 3 هستند باز کنیم و تمام اعداد 5 رقمی را که شامل حداقل یک رقم 7 و یک رقم 2 و یک رقم 3 هستند در اختیار داریم و بستن و امتحان کردن هریک از این اعداد 5 رقمی، 6 ثانیه طول بکشد، برای باز کردن این قفل حداکثر چقدر زمان نیاز داریم؟
می خواهیم با ارقام 9 و 8 و 7 و 6 و 5 و 4 و 3 و 2 و1 رمزهای 5 رقمی بسازیم که شامل حداقل یک رقم 2 و یک رقم 3 و یک رقم 7 باشد. بدون در نظر گرفتن شرط وجود حداقل یک رقم اعداد گفته شده، یعنی در حالت کلی 95 رمز می توان ساخت. به عبارت دیگر: \(\left| S \right| = {9^5}\)
مجموعه رمزهای فاقد رقم 2 را با A و مجموعه رمزهای فاقد 3 را با B و مجموعه رمزهای فاقد 7 را با C نمایش می دهیم؛ بنابراین:
\(\begin{array}{l}\left| A \right| = \left| B \right| = \left| C \right| = {8^5}\\\left| {A \cap B} \right| = \left| {A \cap C} \right| = \left| {B \cap C} \right| = {7^5}\\\left| {A \cap B \cap C} \right| = {6^5}\\\left| {A \cup B \cup C} \right| = 3 \times {8^5} - 3 \times {7^5} + {6^5}\\ \Rightarrow \left| {\overline A \cap \overline B \cap \overline C } \right| = \left| {\overline {A \cup B \cup C} } \right| = \left| S \right| - \left| {A \cup B \cup C} \right| = {9^5} - (3 \times {8^5} - 3 \times {7^5} + {6^5}) = 3390\end{array}\)
حال در صورتی که امتحان کردن هر 5 رقمی 6 ثانیه طول بکشد، حداکثر 20340=6×3390 ثانیه معادل 5 ساعت و 39 دقیقه وقت لازم است.
5 چه تعداد تابع چون \(f:\;A \to B\) می توان تعریف کرد اگر بدانیم |A| = 5 و |B| = 4 است؟ چه تعداد از این توابع یک به یک هستند؟
تعداد توابع مورد نظر است با 45 که هیچکدام از آن ها یک به یک نیست؛ زیرا تعداد اعضای دامنه تابع (A) بیشتر از تعداد اعضای هم دامنه تابع (B) است.
6 به چند طریق می توان 5 کتاب مختلف را بین 8 نفر توزیع کرد، اگر بخواهیم به هر نفر حداکثر یک کتاب بدهیم؟
روش اول:

روش دوم :
تعداد حالت های ممکن برابر است با تعداد توابع یک به یک از مجموعه ای 5 عضوی به یک مجموعه 8 عضوی
\({(8)_5} = P(8\;,\;5) = \frac{{8!}}{{3!}}\)
7 به چند طریق می توان 6 فیلم سینمایی را بین سه داور برای داوری تقسیم کرد، به طوریکه هر داور حداقل یک فیلم را داوری کند؟
تعداد این حالت ها برابر است با تعداد توابع پوشا از یک مجموعه 6 عضوی به یک مجموعه 3 عضوی.
با فرض \(X = \left\{ {{x_1}\;,\;{x_2}\;,\;{x_3}\;,\;{x_4}\;,\;{x_5}\;,\;{x_6}} \right\}\) و \(Y = \left\{ {{y_1}\;,\;{y_2}\;,\;{y_3}} \right\}\)، تعداد توابع پوشا از X به Y را محاسبه می کنیم.
\( = S \Rightarrow \left| S \right| = {3^6}\) مجموعه تمام توابع قابل ساخت از X به Y
\( = A \Rightarrow \left| A \right| = {2^6}\) مجموعه تمام توابعی که برد آن ها \(\left\{ {{y_2}\;,\;{y_3}} \right\}\) می باشد ( برد فاقد عضو \({y_1}\) است).
\( = B \Rightarrow \left| B \right| = {2^6}\) مجموعه تمام توابعی که برد آن ها \(\left\{ {{y_1}\;,\;{y_3}} \right\}\) می باشد ( برد فاقد عضو \({y_2}\) است).
\( = C \Rightarrow \left| C \right| = {2^6}\) مجموعه تمام توابعی که برد آن ها \(\left\{ {{y_1}\;,\;{y_2}} \right\}\) می باشد ( برد فاقد عضو \({y_3}\) است).
\(\begin{array}{l} \Rightarrow \left| {A \cap B} \right| = \left| {A \cap C} \right| = \left| {B \cap C} \right| = 1\quad ,\quad \left| {A \cap B \cap C} \right| = 0\\\\\;\mathop \Rightarrow \limits^{\left| {A \cup B \cup C} \right| = \left| A \right| + \left| B \right| + \left| C \right| - \left| {A \cap B} \right| - \left| {A \cap C} \right| - \left| {B \cap C} \right| + \left| {A \cap B \cap C} \right|} \;\;\left| {A \cup B \cup C} \right| = 3 \times {2^6} - 3 + 0\\\\ \Rightarrow \left| {\overline A \cap \overline B \cap \overline C } \right| = \left| {\overline {A \cup B \cup C} } \right| = \left| S \right| - \left| {A \cup B \cup C} \right| = {3^6} - (3 \times {2^6} - 3) = 540\end{array}\)
8 ثابت کنید، در بین هر 368 نفر حداقل دو نفر هستند که در یک روز متولد شده اند.
در صورتی که هر نفر را به عنوان یک کبوتر و هر روز را یک لانه در نظر بگیریم، می خواهیم 368 کبوتر را در 365 یا 366 لانه ( هر سال 365 روز است به استثناء سال های کبیسه که 366 روز می باشند) جای دهیم.
لذا طبق اصل لانه کبوتری حداقل دو لانه وجود دارد که حداقل دو کبوتر درون آن قرار خواهد گرفت، به عبارت دیگر حداقل 2 نفر هستند که در یک روز سال متولد شده اند.
9 ثابت کنید، اگر در یک دبیرستان حداقل 505 دانش آموز مشغول تحصیل باشند لااقل 7 نفر از آنها روز هفته و ماه تولدشان یکسان است.
منظور از یکسان بودن روزِ هفته و ماه تولد آن است که ایام طبق اعضای مجموعه زیر ر نظر گرفته شده اند:
(فروردین و جمعه) ، ... ، (فروردین و دوشنبه) ، (فروردین و یکشنبه) ، (فروردین و شنبه)}
{(اسفند و جمعه) ، ... ، (اردیبهشت و شنبه) ،
که هر عضو به عنوان یک لانه محسوب شده و در نتیجه 84 = 12 × 7 لانه داریم.
حال در صورتی که هر دانش آموز را به عنوان یک کبوتر، در نظر بگیریم، 505 کبوتر داریم. بنابراین:
\(505 = k \times 84 + 1 \Rightarrow k = 6 \Rightarrow k + 1 = 7 \Rightarrow \)
حداقل 7 نفر از آن ها روز هفته و ماه تولدشان یکسان است.
10 حداقل چند نفر در یک سالن ورزشی مشغول تماشای مسابقه کشتی باشند تا مطمئن باشیم لااقل 20 نفر از آنها روز تولدشان یکسان است؟
برای سهولت در حل مسئله، سال را غیر کبیسه در نظر می گیریم:
\(\left. \begin{array}{l}k + 1 = 20 \Rightarrow k = 19\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;n = 365\end{array} \right\}\;\;\mathop \Rightarrow \limits^{n\;k + 1} \)
حداقل 6936 = 1 + 19 × 365 نفر، تماشاگر مسابقه کشتی هستند.
11 ثابت کنید در بین هر سه عدد طبیعی حداقل دو عدد طبیعی وجود دارد که مجموعشان عددی زوج باشد.
می دانیم باقیمانده هر عدد طبیعی بر 2، برابر 0 یا 1 می باشد.
اگر سه عدد طبیعی را به عنوان کبوترها و باقی مانده تقسیم اعداد طبیعی بر 2 ( یعنی 0 و 1) را به عنوان 2 لانه در نظر بگیریم، طبق اصل لانه کبوتری، حداقل دو کبوتر در یک لانه جای خواهند گرفت، یعنی حداقل دو عدد طبیعی از بین اعداد انتخابی، باقیمانده یکسان در تقسیم بر 2 دارند.
حال این دو عدد که باقیمانده یکسان دارند، هر دو فرد یا هر دو زوج خواهند بود، که در هر صورت مجموعشان عددی زوج است.
1٢ مجموعه اعداد {A={1, 2, ..., 84 را در نظر می گیریم. نشان دهید هر زیر مجموعه 43 عضوی از A دارای حداقل 2 عضو است که مجموعشان برابر با 85 باشد.
اعداد مجموعه B در 42 قفس به شکل زیر افراز می کنیم:
\(\left\{ {1\;,\;84} \right\}\;,\;\left\{ {2\;,\;83} \right\}\;,\;\left\{ {3\;,\;82} \right\}\;,\; \cdots \;,\;\left\{ {42\;,\;43} \right\}\)
قفس ها را به عنوان لانه ها و اعداد درون آن ها را کبوتر در نظر می گیریم، به طوری که می خواهیم از این لانه ها 43 کبوتر به عنوان یک زیر مجموعه 43 عضوی انتخاب کنیم.
طبق اصل لانه کبوتری، حداقل دو کبوتر از یک لانه برداشته خواهند شد، یعنی حداقل دو عدد در زیر مجموعه وجود دارند که مجموع آن ها 85 است.
13 مجموعه اعداد { A={1, 5, 9, 13, ..., 77, 81, 85را که به صورت یک تصاعد عددی مرتب شده اند، در نظر می گیریم. اگر از این مجموعه 13 عضو انتخاب کنیم، نشان دهید که حداقل 2 عدد در این 13 عدد وجود دارد که مجموعشان برابر با 90 باشد.
مجموعه A را به 13 زیرمجموعه به شکل زیر افراز می کنیم:
\(\begin{array}{l}{A_1} = \left\{ {1\;,\;84} \right\}\;\;,\;\;{A_2} = \left\{ {9\;,\;81} \right\}\;,\\{A_3} = \left\{ {13\;,\;77} \right\}\;\;,\;\;{A_4} = \left\{ {17\;,\;73} \right\}\;,\\\\{A_5} = \left\{ {21\;,\;69} \right\}\;\;,\;\;{A_6} = \left\{ {25\;,\;65} \right\}\;,\\\\{A_7} = \left\{ {29\;,\;61} \right\}\quad ,\quad \;{A_8} = \left\{ {33\;,\;57} \right\}\;,\\\\{A_9} = \left\{ {37\;,\;53} \right\}\;\;,\;\;{A_{10}} = \left\{ {41\;,\;49} \right\}\;,\\\\{A_{11}} = \left\{ {45} \right\}\;\;,\;\;{A_{12}} = \left\{ 1 \right\}\end{array}\)
همانطور که مشاهده می شود مجموع اعداد درون زیر مجموعه های دو عضوی برابر 90 است.
زیر مجموعه های فوق را به عنوان 12 لانه در نظر می گیریم که می خواهیم 13 کبوتری از درون آن ها انتخاب کنیم، طبق اصل لانه کبوتری حداقل یکی از لانه ها 2 کبوتر انتخاب خواهد شد، یعنی حداقل دو عدد انتخاب شده از یک زیر مجموعه هستند. واضح است که مجموع آن دو برابر 90 است.
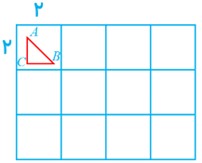
14 13 نقطه درون یک مستطیل 8×6 قرار دارند. نشان دهید حداقل 2 نقطه از این 13 نقطه وجود دارد که فاصله آنها از هم، کمتر از \(\sqrt 8 \) باشد.
مطابق شکل، مستطیل را به 12 مربع به ضلع 2 تقسیم می کنیم و هر کدام از آن ها را به عنوان یک لانه در نظر می گیریم.
در صورتی که هر نقطه را به عنوان یک کبوتر فرض کنیم، می خواهیم 13 کبوتر را در 12 لانه جای دهیم. طبق اصل لانه کبوتری، حداقل دو کبوتر در یک لانه جای می گیرند، یعنی حداقل دو نقطه مانند A و B در یک مربع واقع خواهند شد.
حال طبق قضیه فیثاغورث:
\(\begin{array}{l}A{B^2} = A{C^2} + B{C^2}\;\;\mathop \Rightarrow \limits_{BC < 2}^{AC < 2} \;\;A{B^2} < {2^2} + {2^2}\\\\ \Rightarrow A{B^2} < 8 \Rightarrow AB < \sqrt 8 \end{array}\)
15 نقطه در صفحه با مختصات صحیح در نظر می گیریم. ثابت کنید حداقل دو نقطه از این 5 نقطه وجود دارد، طوری که مختصات نقطه وسط این دو نقطه نیز صحیح می باشد.
پنج نقطه با مختصات های صحیح را به عنوان 5 کبوتر معرفی می کنیم.
برای هر نقطه با مختصات صحیح یکی از چهار حالت زیر وجود دارد، که اگر به عنوان چهار لانه در نظر گرفته شوند.

طبق اصل لانه کبوتری حداقل دو کبوتر در یک لانه جای می گیرند، یعنی حداقل دو نقطه از آن نقاط از نظر زوج یا فرد بودن مختصات شبیه هم خواهند بود. پس مجموع طول های آن ها زوج و مجموع عرض های آن ها نیز زوج است؛ در نتیجه مختصات نقطه وسط صحیح خواهد شد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















