جواب فعالیت صفحه 77 درس 3 ریاضیات گسسته (ترکیبیّات (شمارش))
تعداد بازدید : 84.74Mپاسخ فعالیت صفحه 77 ریاضیات گسسته
-گام به گام فعالیت صفحه 77 درس ترکیبیّات (شمارش)
-فعالیت صفحه 77 درس 3
-شما در حال مشاهده جواب فعالیت صفحه 77 ریاضیات گسسته هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
اگر f تابعی از مجموعه A به مجموعه B باشد و |A|=m و |B|=n در این صورت برای هر \({a_i} \in A\) که \(1≤i≤m \) می توان به n طریق (f(ai را تعریف کرد (f(ai) =b1 یا f(ai) =b2 یا ... یا f(ai) =bn) و لذا طبق اصل ضرب تعداد کل توابع از A به B برابر است با: \({\left| B \right|^{\left| A \right|}} = {n^m}\) حال اگر |A|=5 و |B|=3 در این صورت می خواهیم تعداد توابعی چون f از A به B را تعیین کنیم به طوری که Rf=B (روی تمام اعضای B پیکانی رسم شده باشد، به چنین تابع هایی، تابع پوشا گفته می شود).
1- اگر فرض کنیم {B={b1 , b2 , b3 و {A={a1 , a2 , a3 , a4 , a5 تعریف کنیم،
\(\begin{array}{l}{A_1} = \left\{ {f:A \to B|f\left( {{a_i}} \right) \ne {b_1}\;;\;1 \le i \le 5} \right\}\\\\{A_2} = \left\{ {f:A \to B|f\left( {{a_i}} \right) \ne {b_1}\;;\;1 \le i \le 5} \right\}\\\\{A_3} = \left\{ {f:A \to B|f\left( {{a_i}} \right) \ne {b_1}\;;\;1 \le i \le 5} \right\}\end{array}\)
در این صورت A1 مجموعه ای شامل همه تابع هایی از A به B است که حداقل یک پیکان از اعضای A روی b1 می آورند.
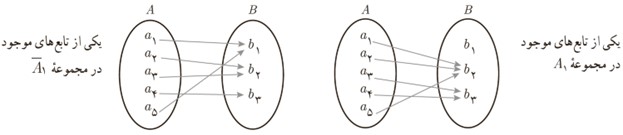
\(\begin{array}{l}{A_1} = \left\{ {f:A \to B|f\left( {{a_i}} \right) \ne {b_1}\;;\;1 \le i \le 5} \right\}\\\\{A_2} = \left\{ {f:A \to B|f\left( {{a_i}} \right) \ne {b_2}\;;\;1 \le i \le 5} \right\}\\\\{A_3} = \left\{ {f:A \to B|f\left( {{a_i}} \right) \ne {b_3}\;;\;1 \le i \le 5} \right\}\end{array}\)
٢ مجموعه \(\left( {\overline {{A_1}} \cap \overline {{A_2}} \cap \overline {{A_3}} } \right) = \left( {\overline {{A_1} \cup {A_2} \cup {A_3}} } \right)\) را تعریف کنید و با استفاده از نتیجه اصل شمول، پاسخ را بیابید.
\(\begin{array}{l}\left| S \right| = {3^{\;...}} = \;...\;,\;\left| {{A_1}} \right| = \left| {{A_2}} \right| = \left| {{A_3}} \right| = {2^{\;...}} = \;...\\\\\left| {{A_1} \cap {A_2}} \right| = \left| {{A_1} \cap {A_3}} \right| = \left| {{A_2} \cap {A_3}} \right| = ...\;,\;\left| {{A_1} \cap {A_2} \cap {A_3}} \right| = 0\\\\\left( {\overline {{A_1} \cup {A_2} \cup {A_3}} } \right) = \left| S \right| - \left| {{A_1} \cup {A_2} \cup {A_3}} \right|\\\\ = 243 - \left( {\;...\; + \;...\; + \;...\; - \;...\; - \;...\; - \;...\; + \;...} \right) = \;...\end{array}\)
\(\begin{array}{l}\left| S \right| = {3^5} = 243\;,\;\left| {{A_1}} \right| = \left| {{A_2}} \right| = \left| {{A_3}} \right| = {2^5} = \;32\\\\\left| {{A_1} \cap {A_2}} \right| = \left| {{A_1} \cap {A_3}} \right| = \left| {{A_2} \cap {A_3}} \right| = 1\;,\;\left| {{A_1} \cap {A_2} \cap {A_3}} \right| = 0\\\\\left( {\overline {{A_1} \cup {A_2} \cup {A_3}} } \right) = \left| S \right| - \left| {{A_1} \cup {A_2} \cup {A_3}} \right|\\\\ = 243 - \left( {32 + 32 + 32 - 1 - 1 - 1 + 0} \right) = \;150\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















