دانلود اپلیکیشن
مفاهیم و مهارت ها
در این فصل اصطلاحات زیر به کار رفته اند.مطمئن شوید که می توانید با جمله های خود، آنها را توصیف کنید و برای هر کدام مثالی بزنید.
1 چندضلعی محدّب
2 چندضلعی مقعّر
3 مرکز تقارن
4 چندضلعی منتظم
5 زاویهٔ داخلی
6 زاویهٔ خارجی
1 چندضلعی محدّب
چندضلعی‌ای است که هیچ‌کدام از زاویه‌های آن بیشتر از ۱۸۰ درجه نباشد (یعنی فرورفتگی یا «غار» نداشته باشد).
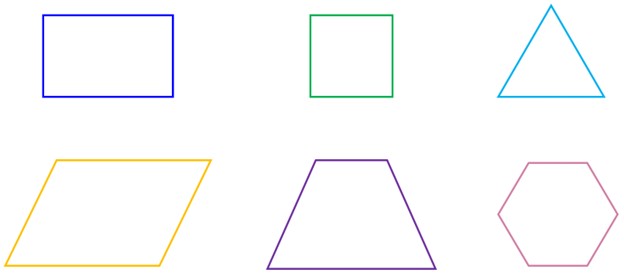
2 چندضلعی مقعّر
برعکس محدب، حداقل یک زاویه بزرگ‌تر از ۱۸۰ درجه دارد (انگار یک قسمت آن به داخل فرو رفته است).
3 مرکز تقارن
نقطه‌ای است که اگر شکل را حول آن ۱۸۰ درجه بچرخانیم، شکل دقیقاً روی خودش می‌افتد.
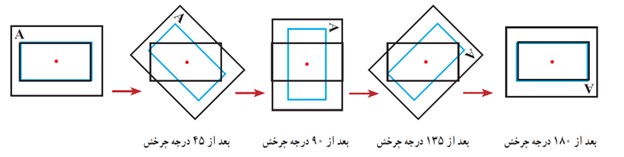
4 چندضلعی منتظم
یک شکل ایده‌آل است! هم تمام ضلع‌هایش با هم مساوی‌اند و هم تمام زاویه‌هایش.
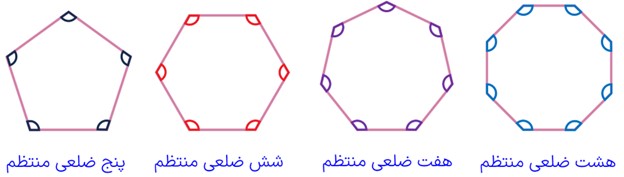
نکته
لوزی منتظم نیست (چون زاویه‌هایش برابر نیستند)، مستطیل هم منتظم نیست (چون ضلع‌هایش برابر نیستند). فقط «مربع» یک چهارضلعی منتظم است.
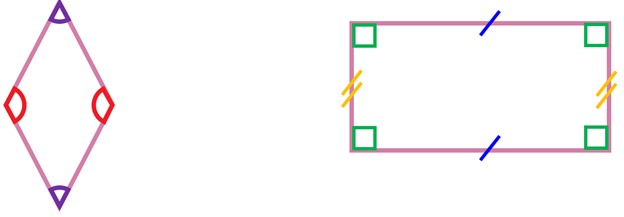
5 زاویهٔ داخلی
زاویه داخلی، زاویه درون شکل است.
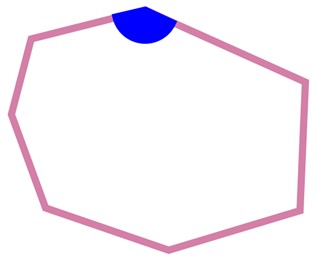
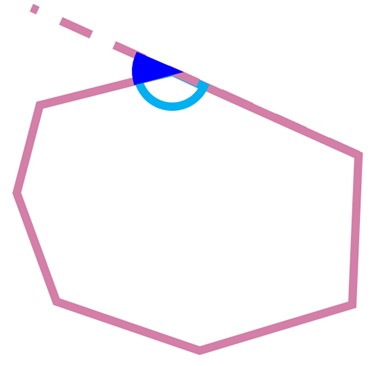
6 زاویهٔ خارجی
زاویه خارجی، زاویه‌ای است که از امتداد دادن یک ضلع با ضلع دیگر در بیرون شکل ساخته می‌شود.
در این فصل، روش های اصلی زیر مطرح شده اند. هر کدام را با یک مثال توضیح دهید و در دفتر خود خلاصهٔ درس را بنویسید.
1 بررسی مرکز تقارن یک شکل
2 پیدا کردن زاویه های مساوی و مکمل در خط های موازی و مورب
3 تعریف متوازی الاضلاع
4 تعریف مستطیل
5 تعریف لوزی
6 تعریف مربع
7 رابطهٔ چهارضلعی ها
8 خاصیت های چهارضلعی ها
9 پیدا کردن مجموع زاویه های داخلی یک چند ضلعی
10 پیدا کردن زاویهٔ داخلی یک چند ضلعی منتظم
11 پیدا کردن مجموع زاویه های خارجی یک چند ضلعی
12 پیدا کردن زاویهٔ خارجی یک رأس مثلث
1 بررسی مرکز تقارن یک شکل
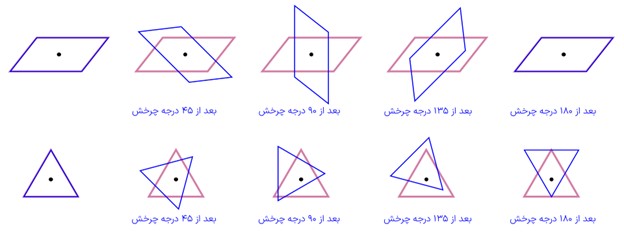
اگر شکلی را حول یک نقطه (مرکز دوران) به اندازه ۱۸۰ درجه بچرخانیم و نتیجهٔ دوران دقیقاً روی خود شکل منطبق شود، می‌گوییم آن شکل مرکز تقارن دارد.
مثال:
متوازی‌الاضلاع دارای مرکز تقارن است، زیرا با چرخش ۱۸۰ درجه حول محل برخورد قطرها، روی خودش می‌افتد. اما مثلث متساوی‌الاضلاع مرکز تقارن ندارد.
2 پیدا کردن زاویه های مساوی و مکمل در خط های موازی و مورب
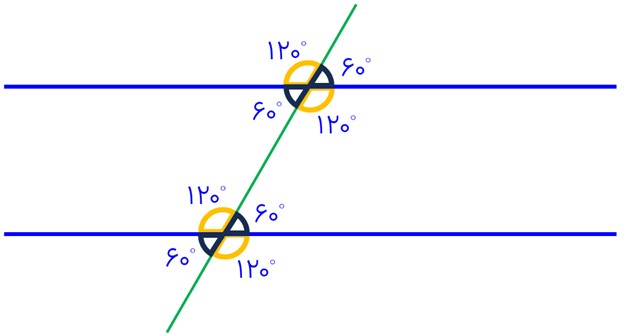
وقتی یک خط مورب دو خط موازی را قطع می‌کند، زاویه‌های تند (حاده) با هم برابرند و زاویه‌های باز (منفرجه) نیز با هم برابرند. همچنین یک زاویه تند و یک زاویه باز مکمل یکدیگرند (مجموعشان ۱۸۰ درجه است).
مثال:
اگر خط مورب با یکی از خطوط موازی زاویه ۶۰ درجه بسازد، تمام زاویه‌های تند ایجاد شده ۶۰ درجه و تمام زاویه‌های باز ۱20 درجه خواهند بود (60 = 120 - 180).
3 تعریف متوازی الاضلاع
چهارضلعی‌ای است که ضلع‌های روبه‌روی آن دو به دو با هم موازی باشند.
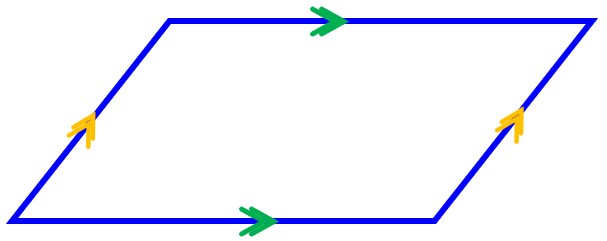
4 تعریف مستطیل
مستطیل، متوازی‌الاضلاعی است که زاویه‌های قائمه (۹۰ درجه) دارد.
نکته
چون مستطیل نوعی متوازی‌الاضلاع است، تمام ویژگی‌های آن را دارد
5 تعریف لوزی
لوزی، متوازی‌الاضلاعی است که چهار ضلع آن با هم برابرند.
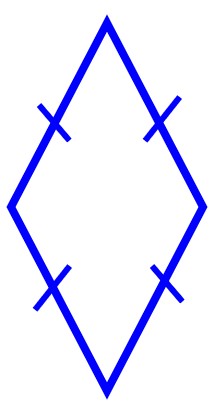
6 تعریف مربع
مربع، متوازی‌الاضلاعی است که هم چهار ضلع مساوی دارد و هم زاویه‌های قائمه دارد.
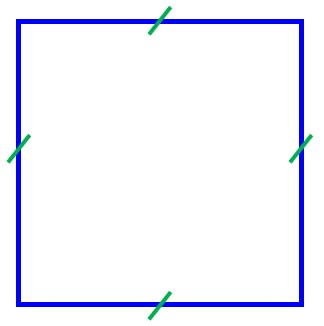
نکته
مربع هم لوزی است (چون ضلع‌های برابر دارد) و هم مستطیل است (چون زاویه‌های قائمه دارد).
7 رابطهٔ چهارضلعی ها
می‌توانیم چهارضلعی‌ها را به صورت مجموعه‌های زیرمجموعه در نظر بگیریم. همه مربع‌ها، مستطیل‌ها و لوزی‌ها، نوعی متوازی‌الاضلاع هستند.
مثال:
هر مربعی یک لوزی است، اما هر لوزی‌ای مربع نیست (مگر اینکه زاویه ۹۰ درجه داشته باشد).
8 خاصیت های چهارضلعی ها
این خاصیت‌ها شامل ویژگی‌های ضلع‌ها، زاویه‌ها و قطرهاست:
متوازی‌الاضلاع: قطرهایش یکدیگر را نصف می‌کنند.
مستطیل: علاوه بر نصف کردن، قطرها با هم برابرند.
لوزی: علاوه بر نصف کردن، قطرها بر هم عمودند.
مربع: قطرها هم مساوی‌اند، هم منصف‌اند و هم بر یکدیگر عمودند.
9 پیدا کردن مجموع زاویه های داخلی یک چند ضلعی
برای یک n ضلعی، از فرمول زیر استفاده می‌کنیم:
\((n - 2) \times {180^ \circ }\)
مثال:
برای یک پنج‌ضلعی :(n=5)
\((5 - 2) \times {180^ \circ } = 3 \times {180^ \circ } = {540^ \circ }\)
10 پیدا کردن زاویهٔ داخلی یک چند ضلعی منتظم
چون در چندضلعی منتظم همه زاویه‌ها با هم برابرند، مجموع زاویه‌ها را بر تعداد اضلاع (n) تقسیم می‌کنیم:
\(\frac{{(n - 2) \times {{180}^ \circ }}}{n}\)
مثال:
اندازه هر زاویه یک ۶ضلعی منتظم:
\(\frac{{(6 - 2) \times {{180}^ \circ }}}{6} = \frac{{{{720}^ \circ }}}{6} = {120^ \circ }\)
11 پیدا کردن مجموع زاویه های خارجی یک چند ضلعی
مجموع زاویه‌های خارجی هر چندضلعی محدب ، همواره برابر با ۳۶۰ درجه است و به تعداد اضلاع بستگی ندارد.
12 پیدا کردن زاویهٔ خارجی یک رأس مثلث
در هر مثلث، اندازه هر زاویه خارجی برابر است با مجموع دو زاویه داخلیِ غیر مجاور آن.
مثال:
اگر دو زاویه داخلی یک مثلث ۵۰ و ۶۰ درجه باشند، زاویه خارجی رأس سوم برابر است با:
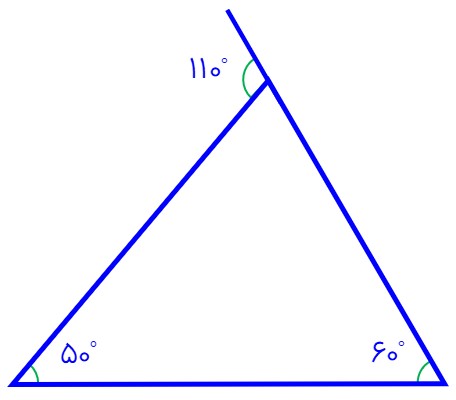
\({50^ \circ } + {60^ \circ } = {110^ \circ }\)
کاربرد
این درس به شما در درک بهتر شکل های هندسی و رابطهٔ بین آنها کمک می کند. ما در انواع صنایع دستی و آثار معماری کشور خود شکل های مختلف هندسی را می توانیم ببینیم.
تمرین های ترکیبی
1 هر خانهٔ جدول زیر را با علامت × یا P کامل کنید.
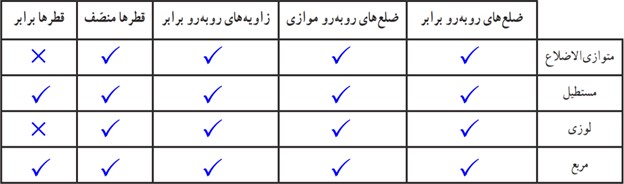
2 اندازهٔ زاویه های داخلی و خارجی یک هشت ضلعی منتظم را پیدا کنید.
\( = \frac{{(n - 2) \times {{180}^ \circ }}}{n} = \frac{{(8 - 2) \times {{180}^ \circ }}}{8} = {135^ \circ }\) زاویه داخلی
\( = \frac{{{{360}^ \circ }}}{n} = \frac{{{{360}^ \circ }}}{8} = {45^ \circ }\) زاویه خارجی
1736019749.png)
