1736019749.png)
جواب فعالیت صفحه 31 درس 3 ریاضی هشتم (چندضلعی ها)
تعداد بازدید : 78.8Mپاسخ فعالیت صفحه 31 ریاضی هشتم
-گام به گام فعالیت صفحه 31 درس چندضلعی ها
-فعالیت صفحه 31 درس 3
-شما در حال مشاهده جواب فعالیت صفحه 31 ریاضی هشتم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
1 یک ورق کاغذ پوستی روی مستطیل روبه رو قرار دهید و تصویر مستطیل را روی آن رسم کنید.
نوک مدادتان را روی مرکز دوران بگذارید و مانند شکل های زیر، کاغذ پوستی را 180 درجه حول مرکز دوران بچرخانید.
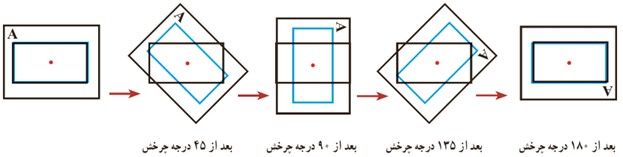
آیا تصویر، روی شکل منطبق می شود؟
بله، تصویر بر روی شکل منطبق می شود.
اگر شکلی را حول یک نقطه، ١٨٠ درجه دوران دهیم و نتیجه دوران، روی خودش منطبق شود، می گوییم شکل مرکز تقارن دارد و نقطهٔ مورد نظر، مرکز تقارن شکل است.
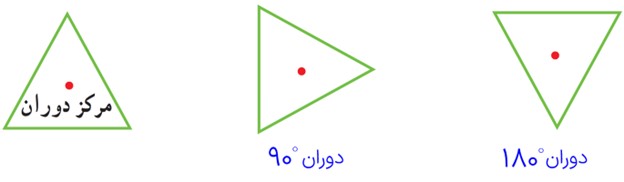
2 شکل روبه رو مثلثی متساوی الاضلاع است. یک ورق کاغذ پوستی روی آن قرار دهید و مراحل فعّالیت (1) را تکرار کنید. آیا تصویر، روی شکل منطبق می شود؟ چه نتیجه ای می گیرید؟
خیر؛ نقطه مشخص شده مرکز تقارن شکل نیست:
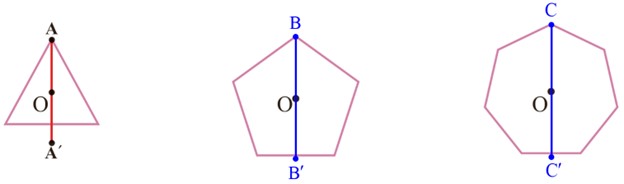
3 در کدام یک از چندضلعی های منتظم زیر، نقطهٔ مشخص شده مرکز تقارن است؟
به نظر شما نُه ضلعی منتظم مرکز تقارن دارد؟
ده ضلعیِ منتظم چطور؟ از این فعّالیت چه نتیجه ای می گیرید؟
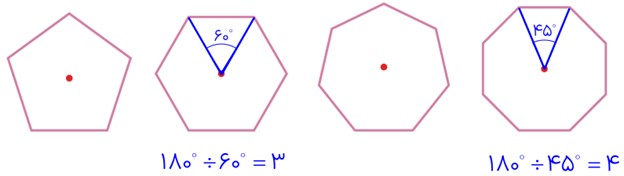
در شش ضلعی و هشت ضلعی منتظم، نقطۀ مشخص شده مرکز تقارن است.
نُه ضلعی منتظم مرکز تقارن ندارد.
ده ضلعی منتظم مرکز تقارن دارد.
نتیجه
اگر n زوج باشد، آنگاه هر n ضلعی منتظم مرکز تقارن دارد.
4 یکی از راه های تشخیص اینکه نقطهٔ O در مثلث متساوی الاضلاع مرکز تقارن نیست، این است که می توان روی شکل، نقطه ای پیدا کرد که قرینهٔ آن نسبت به نقطهٔ O روی خود شکل قرار نگرفته باشد. مانند نمونه، نشان دهید که نقطهٔ O در دو شکل دیگر هم، مرکز تقارن نیست.
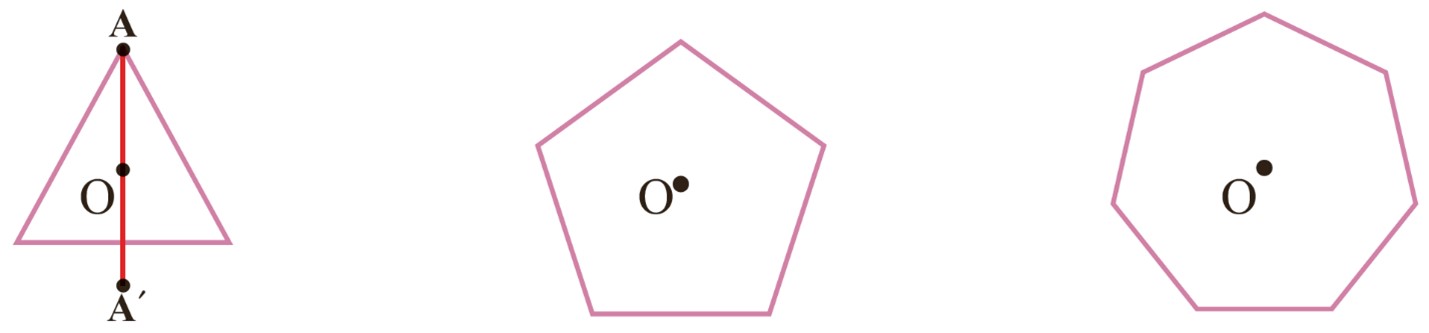
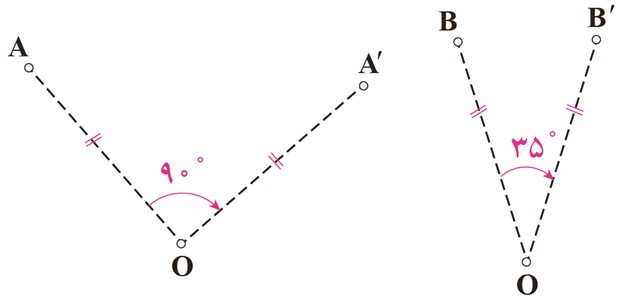
5 شکل های مقابل چگونگی پیدا کردن دوران یافتهٔ نقاط A و B حول مرکز O را به اندازۀ \({90^ \circ }\) و \({35^ \circ }\) در جهت عقربه های ساعت نشان می دهد.
کدام یک از شکل های فعّالیت (3) با دوران \({90^ \circ }\) حول نقطهٔ مشخص شده در جهت عقربه های ساعت روی خودش می افتد؟
8 ضلعی منتظم
نکته
هر n ضلعی منتظم با دوران هایی که مضرب \(\frac{{{{360}^ \circ }}}{n}\) باشد، بر روی خودش منطبق می شود؛ مثلاً هر 10 ضلعی منتظم با هر دوران که مضربی از \({36^ \circ }\) باشد، بر روی خودش منطبق می شود.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
