گام به گام تمرین صفحه 29 درس 1 هندسه (2) (دایره)

1)

فرض: ذوزنقه متساوی الساقین است.

حکم: ذوزنقه محاطی است.

-اثبات:

\(\left. \begin{array}{l}\widehat A + \widehat D = {180^ \circ }\;,\;\widehat C = \widehat D \Rightarrow \widehat A + \widehat C = {180^ \circ }\\\widehat A + \widehat D = {180^ \circ }\;,\;\widehat A = \widehat B \Rightarrow \widehat B + \widehat D = {180^ \circ }\end{array} \right\} \Rightarrow \)

ذوزنقه ABCD محاطی است

فرض: ذوزنقه محاطی است.

حکم: ذوزنقه متساوی الساقین است.

-اثبات:

\(AB\parallel DC\;,\;AD\) مورب

طبق قضیه خطوط موازی

\(\begin{array}{l}\left. \begin{array}{l}\widehat A + \widehat D = {180^ \circ }\\\widehat A + \widehat C = {180^ \circ }\end{array} \right\}\\ \Rightarrow \widehat A + \widehat D = \;{\kern 1pt} \widehat A + \widehat C \Rightarrow \;{\kern 1pt} \widehat C = \widehat D\end{array}\)

طبق قضیه زاویه های مکمل

\(\Rightarrow \;{\kern 1pt} \widehat A = \widehat B\)

2)

مرکز دایره محیطی، نقطه O محل برخورد عموئمنصف های اضلاع مثلث است و چون مثلث متساوی الاضلاع است، نقطه O محل برخورد میانه ها هم است. بنابراین :

\(\begin{array}{l}{S_{A\mathop B\limits^\Delta  C}} = \frac{{\sqrt 3 }}{4}{a^2} = 3{S_{O\mathop B\limits^\Delta  C}}\\ \Rightarrow 3 \times \frac{{OH \cdot a}}{2} = \frac{{\sqrt 3 }}{4}{a^2}\\ \Rightarrow OH = \frac{{\sqrt 3 }}{6}a\\\\{S_{A\mathop B\limits^\Delta  C}} = \frac{{\sqrt 3 }}{4}{a^2} = \frac{{AH \cdot a}}{2}\\ = \frac{{(AO + OH) \cdot a}}{2} = \frac{{(R + \frac{{\sqrt 3 }}{6}a) \cdot a}}{2}\\ \Rightarrow R + \frac{{\sqrt 3 }}{6}a = \frac{{\sqrt 3 }}{2}a\\ \Rightarrow R = \frac{{\sqrt 3 }}{3}a \Rightarrow a = \sqrt 3 R\\ \Rightarrow {S_{A\mathop B\limits^\Delta  C}} = \frac{{3\sqrt 3 }}{4}{R^2}\end{array}\)

3)

فرض نیمساز زاویه BAC، دایره محیطی را در نقطه D قطع می کند:

\(\widehat {BAD} = \widehat {CAD}\) , مثلث محاطی

\(\Rightarrow \widehat {BD} = \widehat {CD}\) , قضیه کمان ها و وترهای مساوی

\(\Rightarrow BD = CD\)

فاصله نقطه D از دو نقطه B و C به یک اندازه است، پس بنا بر خاصیت عمودمنصف نقطه D روی عمودمنصف پاره خط BC نیز قرار دارد.

4)

چون ذوزنقه ABCD محاطی است، پس متساوی الساقین است و چون محیطی است مجموع دو ضلع مقابل برابر است. در نتیجه:

\(2c = a + b\)

و مثلث ADF قائم الزاویه است.

\(\begin{array}{l}2c = a + b \Rightarrow c = \frac{{a + b}}{2}\quad ,\quad \\b = 2x + a \Rightarrow x = \frac{{b - a}}{2}\\{h^2} = {c^2} - {x^2} \Rightarrow \\{h^2} = {(\frac{{a + b}}{2})^2} - {(\frac{{b - a}}{2})^2}\\ \Rightarrow {h^2} = \frac{{4ab}}{4} \Rightarrow h = \sqrt {ab} \\{S_{ABCD}} = \frac{1}{2}(a + b) \times h\\ \Rightarrow {S_{ABCD}} = \frac{1}{2}(a + b)\sqrt {ab} \end{array}\)

5)

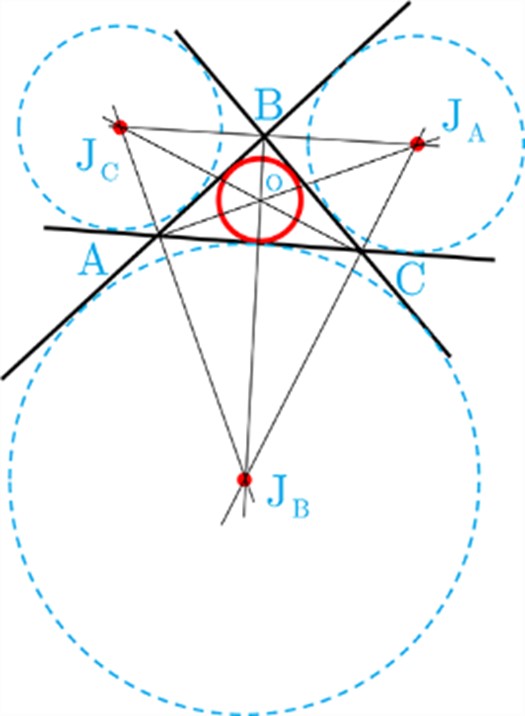
\(\begin{array}{l}\left. \begin{array}{l}S = {S_{A\mathop B\limits^\Delta  C}}\\P = \left( {a + b + c} \right) = 2p \Rightarrow p = \frac{{a + b + c}}{2}\end{array} \right\}\\ \Rightarrow S = rp \Rightarrow \frac{1}{r} = \frac{p}{S}\\\\{r_a} = \frac{S}{{p - a}} \Rightarrow \frac{1}{{{r_a}}} = \frac{{p - a}}{S}\\{r_b} = \frac{S}{{p - b}} \Rightarrow \frac{1}{{{r_b}}} = \frac{{p - b}}{S}\\{r_c} = \frac{S}{{p - c}} \Rightarrow \frac{1}{{{r_c}}} = \frac{{p - c}}{S}\\\\\frac{1}{{{r_a}}} + \frac{1}{{{r_b}}} + \frac{1}{{{r_c}}} = \frac{{p - a}}{S} + \frac{{p - b}}{S} + \frac{{p - c}}{S} = \frac{{3p - \left( {a + b + c} \right)}}{S}\\\begin{array}{*{20}{c}}{}&{}&{}\end{array}\quad \;\, = \frac{{3p - 2p}}{S} = \frac{p}{S} = \frac{1}{r} \Rightarrow \frac{1}{{{r_a}}} + \frac{1}{{{r_b}}} + \frac{1}{{{r_c}}} = \frac{1}{r}\end{array}\)

\(\begin{array}{l}\left. \begin{array}{l}S = \frac{1}{2}a \cdot {h_a} \Rightarrow {h_a} = \frac{{2S}}{a} \Rightarrow \frac{1}{{{h_a}}} = \frac{a}{{2S}}\\S = \frac{1}{2}b \cdot {h_b} \Rightarrow {h_b} = \frac{{2S}}{b} \Rightarrow \frac{1}{{{h_b}}} = \frac{b}{{2S}}\\S = \frac{1}{2}c \cdot {h_c} \Rightarrow {h_c} = \frac{{2S}}{c} \Rightarrow \frac{1}{{{h_c}}} = \frac{c}{{2S}}\end{array} \right\}\\\\ \Rightarrow \begin{array}{*{20}{c}}{\frac{1}{{{h_a}}} + \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}} = \frac{a}{{2S}} + \frac{b}{{2S}} + \frac{c}{{2S}}\quad \begin{array}{*{20}{c}}{}&{}&{}\end{array}}\\{\begin{array}{*{20}{c}}{}&{}&{}&{}\end{array}\;\;\, = \frac{{a + b + c}}{{2S}} = \frac{{2p}}{{2S}} = \frac{p}{S} = \frac{1}{r}}\end{array}\end{array}\)

6)

\({P_{A\mathop B\limits^\Delta  C}} = 2P = \left( {a + b + c} \right) \Rightarrow P = \frac{{a + b + c}}{2}\)

\(AM = AN = P – a\)

\(\begin{array}{l}\left. \begin{array}{l}AN = c - BN\\AM = b - CM\end{array} \right\}\\ \Rightarrow AM + AN = b + c - \left( {BN + CM} \right)\;,\\AM = AN\;\;,\;\;CM = CK\;\;,\;\;BN = BK\\ \Rightarrow 2AM = b + c - \left( {BK + CK} \right)\\ = b + c - a = \left( {a + b + c} \right) - 2a\\\\2AM = 2P - 2a \Rightarrow AM = P - a\end{array}\)

\(BN = BK = P - b\)

\(\begin{array}{l}\left. \begin{array}{l}BN = c - AN\\BK = a - CK\end{array} \right\}\\ \Rightarrow BN + BK = a + c - \left( {AN + CK} \right)\;,\\BK = BN\;,\;AN = AM\;,\;CK = CM\\ \Rightarrow 2BN = a + c - \left( {AM + CM} \right)\\ = a + c - b = \left( {a + b + c} \right) - 2b\\\\2BN = 2P - 2b \Rightarrow BN = P - b\end{array}\)

\(CM = CK = P – c\)

\(\begin{array}{l}\left. \begin{array}{l}CM = b - AM\\CK = a - BK\end{array} \right\}\\ \Rightarrow CM + CK = b + a - \left( {AM + BK} \right)\;,\\CM = CK\;,\;AN = AM\;,\;BK = BN\\ \Rightarrow 2CM = b + a - \left( {AN + BN} \right)\\ = b + a - c = \left( {a + b + c} \right) - 2c\\\\2CM = 2P - 2c \Rightarrow CM = P - c\end{array}\)

\(AT = AT' = P\)

\(\begin{array}{l}AT + AT' = c + BT + b + CT'\;\;,\\AT = AT'\;\;,\;\;BT = BO\;\;\;,\;\;\;CT' = CO\\ \Rightarrow 2AT = c + b + BO + CO = c + b + a = 2P\\ \Rightarrow 2AT = 2P \Rightarrow AT = AT' = P\end{array}\)

7)

\(\begin{array}{l}O\mathop H\limits^\Delta  D:\quad \widehat H = {90^ \circ }\;\;,\;\;OD = r\\ \Rightarrow \sin \frac{{180}}{n} = \frac{{HD}}{r} \Rightarrow 2\sin \frac{{180}}{n} = \frac{{2HD}}{r}\\,\;\;2HD = CD \Rightarrow CD = 2r\sin \frac{{180}}{n}\\\\O\mathop M\limits^\Delta  B:\quad \widehat M = {90^ \circ }\;\;,\;\;OM = r\\ \Rightarrow \tan \frac{{180}}{r} = \frac{{MB}}{r} \Rightarrow 2\tan \frac{{180}}{r} = \frac{{2MB}}{r}\\,\;\;2MB = AB \Rightarrow AB = 2r\tan \frac{{180}}{r}\end{array} \)

8)

الف)

اندازه هر زاویه داخلی شش ضلعی منتظم 120 درجه است. بنابراین زاویه های خارجی 60 درجه است. با توجه به شکل و مجموع زوایای داخلی هر مثلث نتیجه می گیریم که \(\widehat M = \widehat N = \widehat P = {60^ \circ } \) و در نتیجه مثلث MNP متساوی الاضلاع است.

ب)

اگر قطرهای شش ضلعی منتظم را رسم کنیم، آن را به شش مثلث متساوی الاضلاع تقسیم می کنیم و در مثلث MNP ، 9 مثلث همنهشت ایجاد می شود:

\(\frac{{{S_{ABCDEF}}}}{{{S_{M\mathop N\limits^\Delta  P}}}} = \frac{{6{S_{M\mathop A\limits^\Delta  B}}}}{{9{S_{M\mathop A\limits^\Delta  B}}}} = \frac{6}{9} = \frac{2}{3}\)

پ)

مجموع فاصله های هر نقطه درون مثلث متساوی الاضلاع مقداری ثابت است و این مقدار با ارتفاع مثلث برابر است :

\(TH = TH' = TH'' = MM'\)

ت)

مجموع فاصله های هر نقطه درون مثلث متساوی الاضلاع مقداری ثابت است و این مقدار با ارتفاع مثلث برابر است :

\(\begin{array}{l}{S_{T\mathop A\limits^\Delta  F}} + {S_{T\mathop D\limits^\Delta  F}} + {S_{T\mathop B\limits^\Delta  C}} = \frac{1}{2}AF \cdot TH'' + \frac{1}{2}DE \cdot TH' + \frac{1}{2}BC \cdot TH\\,\;\;AF = ED = BC = a\\\\ \Rightarrow {S_{T\mathop A\limits^\Delta  F}} + {S_{T\mathop D\limits^\Delta  F}} + {S_{T\mathop B\limits^\Delta  C}} = \frac{1}{2}a\left( {TH'' + TH' + TH} \right)\\\\ \Rightarrow {S_{T\mathop A\limits^\Delta  F}} + {S_{T\mathop D\limits^\Delta  F}} + {S_{T\mathop B\limits^\Delta  C}} = \frac{1}{2}a \cdot h\\\\{S_{M\mathop N\limits^\Delta  P}} = \frac{1}{2}MN \cdot h\;\;,\;\;MN = 3a \Rightarrow {S_{M\mathop N\limits^\Delta  P}} = \frac{3}{2}a \cdot h\\\\ \Rightarrow \frac{{{S_{T\mathop A\limits^\Delta  F}} + {S_{T\mathop D\limits^\Delta  F}} + {S_{T\mathop B\limits^\Delta  C}}}}{{{S_{M\mathop N\limits^\Delta  P}}}} = \frac{{\frac{1}{2}a \cdot h}}{{\frac{3}{2}a \cdot h}} = \frac{1}{3}\end{array}\)

9)

در چهارضلعی ABCD قطرها یکدیگر را نصف می کنند و با هم برابرند، پس مستطیل است و چون قطرها بر هم عمودند، نتیجه می گیریم که مربع است.

عمودمنصف هر ضلع، نیمساز رأس مقابل نیز است؛ بنابراین:

\(\begin{array}{l}\widehat {{O_1}} = \widehat {{O_2}} = \widehat {{O_3}} = \widehat {{O_4}} = \widehat {{O_5}} = \widehat {{O_6}} = \widehat {{O_7}} = \widehat {{O_8}}\\ \Rightarrow \widehat {AM} = \widehat {MB} = \widehat {BQ} = \widehat {QC} = \widehat {CP} = \widehat {PD} = \widehat {DN} = \widehat {NA}\\ \Rightarrow AM = MB = BQ = QC = CP = PD = DN = NA\end{array}\)