1736019749.png)
جواب سؤال متن صفحه 28 درس 1 هندسه یازدهم (دایره)
تعداد بازدید : 78.78Mپاسخ سؤال متن صفحه 28 هندسه یازدهم
-گام به گام سؤال متن صفحه 28 درس دایره
-سؤال متن صفحه 28 درس 1
-شما در حال مشاهده جواب سؤال متن صفحه 28 هندسه یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
قضیه: یک چهارضلعی محیطی است اگر و فقط اگر مجموع اندازه های دو ضلع مقابل، برابر مجموع اندازه های دو ضلع دیگر باشند.
اساس اثبات بر این است که اگر از نقطه ای بیرون دایره دو مماس بر دایره رسم کنیم دو پاره خط مماس هم اندازه اند.
اثبات
1 اگر چهارضلعی ABCD محیطی باشد، AB+CD=AM+…+PC+…=AQ+…+CN+…=AD+BC عکس این قضیه نیز با برهان خلف ثابت می شود.
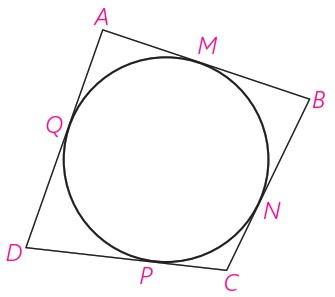
\(B+CD=AM+BM+PC+DP=AQ+BN+CN+DQ=AD+BC\)
2 فرض کنید: AB+CD=BC+AD.
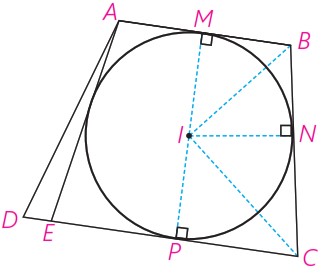
نیمسازهای دو زاویهٔ B و C همدیگر را در نقطه ای مانند I قطع می کنند. با توجه به ویژگی نیمساز، چرا نقطهٔ I از سه ضلع CD و BC و AB به یک فاصله است؟ (IM=IN=IP) چرا دایره ای به مرکز I وشعاع IM بر AB و BC و CD مماس است؟ حال اگر این دایره بر AD هم مماس باشد، حکم ثابت شده است.
اما اگر این دایره بر AD مماس نباشد از A بر آن مماسی رسم می کنیم تا خط CD را در نقطه ای مانند E قطع کند؛ در این صورت E بین P و D یا D بین E و P واقع می شود. پس، AB+EC=AE+BC؛ (چرا؟) از این رابطه با استفاده از رابطه فرض چگونه نتیجه می گیرید: AD=DE+AE ؟
این رابطه امکان ندارد؛ (چرا؟) پس E همان D است و دایره بر ضلع AD نیز مماس است.
نقطه I روی نیمساز زاویه B است؛ پس \(\left( 1 \right)\quad IM = IN\)
نقطه I روی نیمساز زاویه C است؛ پس \(\left( 2 \right)\quad IN = IP\)
از (1) و (2) نتیجه می گیریم که \(IM = IP\)
پس نقطه I از سه ضلع AB و BC و CD به یک فاصله است.
زیرا این شعاع ها در نقاط اشتراک با دایره بر آن عمود هستند.
چهارضلعی ABCE محیطی است، پس بنا بر بند (1) همین قضیه را نتیجه می گیریم که :
\(AB + CE = AE + BC\)
\(\begin{array}{l}\left. \begin{array}{l}AB + CD = AD + BC\\AB + CE = AE + BC\end{array} \right\}\\\\ \Rightarrow CD - CE = AD - AE\\\\ \Rightarrow CD - CE + AE = AD \Rightarrow DE + AE = AD\end{array}\)
بنا بر نامساوی مثلثی، در مثلث ADE داریم: \(DE + AE > AD\)
پس رابطه فوق امکان ندارد، مگر آن که E همان D باشد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
