دانلود اپلیکیشن
1 طرف دیگر تساوی ها را بنویسید.
\(\begin{array}{l}\vec a = \left[ {\begin{array}{*{20}{c}}3\\7\end{array}} \right] = \\\\\vec b = \left[ {\begin{array}{*{20}{c}}{}\\{}\end{array}} \right] = - 2\vec i + 5\vec j\\\\\vec c = \left[ {\begin{array}{*{20}{c}}{}\\{}\end{array}} \right] = 3\vec i - 2\vec j\\\\\vec d = \left[ {\begin{array}{*{20}{c}}{ - 2}\\{ - 4}\end{array}} \right] = \\\\\vec e = \left[ {\begin{array}{*{20}{c}}{ - 5}\\0\end{array}} \right] = \\\\\vec f = \left[ {\begin{array}{*{20}{c}}{}\\{}\end{array}} \right] = - 2\vec j\end{array}\)
\(\begin{array}{l}\vec a = \left[ {\begin{array}{*{20}{c}}3\\7\end{array}} \right] = 3\vec i + 7\vec j\\\\\vec b = \left[ {\begin{array}{*{20}{c}}{ - 2}\\5\end{array}} \right] = - 2\vec i + 5\vec j\\\\\vec c = \left[ {\begin{array}{*{20}{c}}3\\{ - 2}\end{array}} \right] = 3\vec i - 2\vec j\\\\\vec d = \left[ {\begin{array}{*{20}{c}}{ - 2}\\{ - 4}\end{array}} \right] = - 2\vec i - 4\vec j\\\\\vec e = \left[ {\begin{array}{*{20}{c}}{ - 5}\\0\end{array}} \right] = - 5\vec i\\\\\vec f = \left[ {\begin{array}{*{20}{c}}0\\{ - 2}\end{array}} \right] = - 2\vec j\end{array}\)
2 دو محور عمود برهم رسم کنید و بردارهای واحد مختصات را روی آنها مشخص کنید. آنگاه بردارهای زیر را روی آن دستگاه مختصات رسم کنید و هر بردار را برحسب بردارهای واحد i و j بنویسید.
\(\begin{array}{l}\vec a = \left[ {\begin{array}{*{20}{c}}2\\1\end{array}} \right]\\\\\vec b = \left[ {\begin{array}{*{20}{c}}{ - 2}\\3\end{array}} \right]\\\\\vec c = \left[ {\begin{array}{*{20}{c}}5\\{ - 1}\end{array}} \right]\\\\\vec d = \left[ {\begin{array}{*{20}{c}}{ - 6}\\{ - 4}\end{array}} \right]\end{array}\)
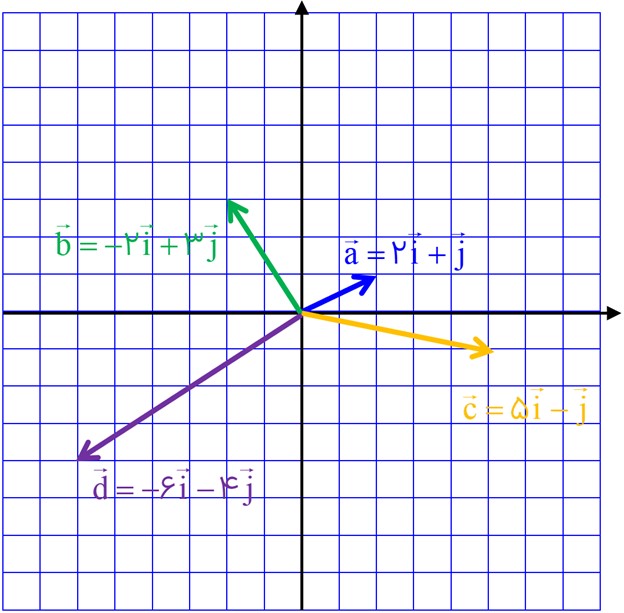
\(\begin{array}{l}\vec a = \left[ {\begin{array}{*{20}{c}}2\\1\end{array}} \right] = 2\vec i + \vec j\\\\\vec b = \left[ {\begin{array}{*{20}{c}}{ - 2}\\3\end{array}} \right] = - 2\vec i + 3\vec j\\\\\vec c = \left[ {\begin{array}{*{20}{c}}5\\{ - 1}\end{array}} \right] = 5\vec i - \vec j\\\\\vec d = \left[ {\begin{array}{*{20}{c}}{ - 6}\\{ - 4}\end{array}} \right] = - 6\vec i - 4\vec j\end{array}\)
3 با توجه به شکل زیر، مختصات بردار c را با دو روش زیر پیدا کنید.
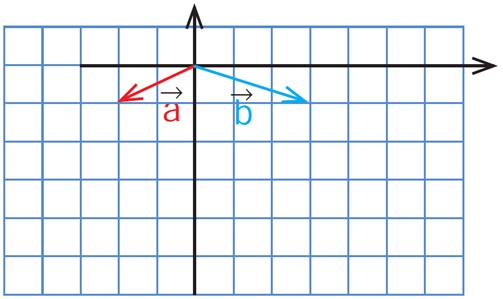
الف رسم شکل و نوشتن مختصات \(\vec c\) از روی شکل
\(\vec c = 3\vec a + 2\vec b = \left[ {\begin{array}{*{20}{c}}{}\\{}\end{array}} \right]\)
ب پیدا کردن مختصات \(\vec a\) و \(\vec b\) و قرار دادن آنها در تساوی زیر.
\(\vec c = 3\vec a + 2\vec b = 3\left[ {\begin{array}{*{20}{c}}{}\\{}\end{array}} \right] + 2\left[ {\begin{array}{*{20}{c}}{}\\{}\end{array}} \right]\)
ویژگی های هر روش را بیان کنید.
کدام روش برای رایانه ای شدن مناسب تر است؟ چرا؟
الف
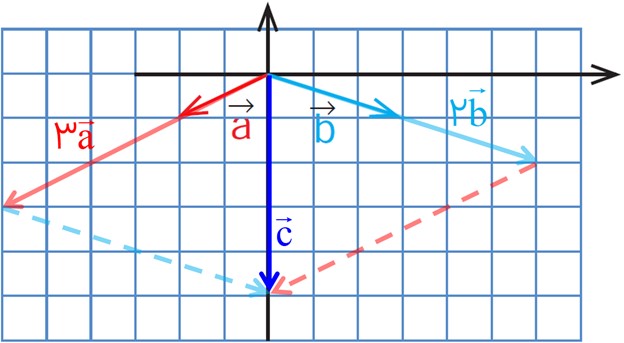
\(\vec c = 3\vec a + 2\vec b = \left[ {\begin{array}{*{20}{c}}0\\{ - 5}\end{array}} \right]\)
این روش را می توان روش هندسی نامید. به دست آوردن جواب از این راه نیاز به رسم دقیق بردارها دارد و نیاز به کمی زمان هست و هنگامی که اعداد بزرگ باشند، ایجاد مشکل می کند.
ب
\(\begin{array}{l}\vec c = 3\vec a + 2\vec b = \\\\3\left[ {\begin{array}{*{20}{c}}{ - 2}\\{ - 1}\end{array}} \right] + 2\left[ {\begin{array}{*{20}{c}}3\\{ - 1}\end{array}} \right] = \\\\\left[ {\begin{array}{*{20}{c}}{ - 6}\\{ - 3}\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}6\\{ - 2}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}0\\{ - 5}\end{array}} \right]\end{array}\)
روش ب را می توان روش جبری نامید که سریع تر و دقیق تر از روش هندسی است و با بزرگ شدن اعداد و مختصات بردارها، هیچ مشکلی ایجاد نمی شود. بنابراین این روش برای رایانه ای شدن مناسب تر است.
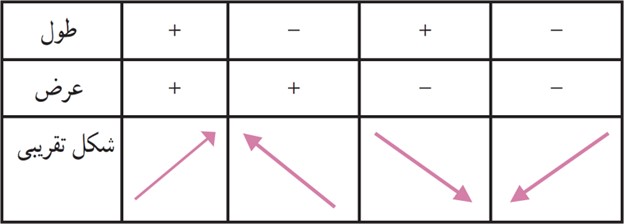
4 با توجه به علامت طول و عرض بردار، شکل تقریبی آن را مانند نمونه رسم کنید.
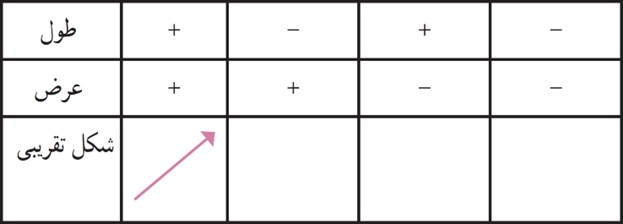
5 اگر \(\vec a = 2\vec i - 3\vec j\) و \(\vec b = \left[ {\begin{array}{*{20}{c}}{ - 1}\\2\end{array}} \right]\) باشد، بردار x را از معادلۀ زیر پیدا کنید.
\(2\vec x - \vec j = 2\vec a - \vec b\)
\(\begin{array}{l}2\vec x - \vec j = 2\vec a - \vec b\\\\ \Rightarrow 2\vec x - \vec j = 2(2\vec i - 3\vec j) - \left[ {\begin{array}{*{20}{c}}{ - 1}\\2\end{array}} \right]\\\\ \Rightarrow 2\vec x - \vec j = 2(2\vec i - 3\vec j) - ( - \vec i + 2\vec j)\\\\ \Rightarrow 2\vec x - \vec j = 4\vec i - 6\vec j + \vec i - 2\vec j\\\\ \Rightarrow 2\vec x - \vec j = 5\vec i - 8\vec j\\\\ \Rightarrow 2\vec x = 5\vec i - 8\vec j + \vec j\\\\ \Rightarrow 2\vec x = 5\vec i - 7\vec j\\\\ \Rightarrow \vec x = \frac{5}{2}\vec i - \frac{7}{2}\vec j = \left[ {\begin{array}{*{20}{c}}{\frac{5}{2}}\\{ - \frac{7}{2}}\end{array}} \right]\end{array}\)
6 یک روباتِ برنامه ریزی شده به صورت زیر از مبدأ مختصات حرکت می کند.
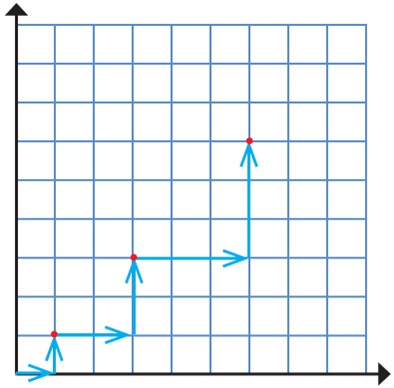
با مشاهدهٔ سه حرکت اولِ این روبات، الگویی برای حرکت آن کشف کنید و توضیح دهید. روبات پس از حرکت پنجم به کدام نقطه می رسد؟
در هر مرحله، یک واحد به مختصات طولی و عرضی حرکت اضافه شده است. در حرکت اول ربات در نقطه \(\left[ {\begin{array}{*{20}{c}}1\\1\end{array}} \right]\)، در حرکت دوم در نقطه \(\left[ {\begin{array}{*{20}{c}}{1 + 2}\\{1 + 2}\end{array}} \right]\) و در حرکت سوم \(\left[ {\begin{array}{*{20}{c}}{1 + 2 + 3}\\{1 + 2 + 3}\end{array}} \right]\) قرار دارد.
به طور کلی بعد از x بار حرکت، ربات به نقطۀ رو به رو می رسد:
\(\left[ {\begin{array}{*{20}{c}}{1 + 2 + 3 + \cdots + x}\\{1 + 2 + 3 + \cdots + x}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{\frac{{x(x + 1)}}{2}}\\{\frac{{x(x + 1)}}{2}}\end{array}} \right]\)
پس بعد از حرکت پنجم به نقطۀ \(\left[ {\begin{array}{*{20}{c}}{15}\\{15}\end{array}} \right]\) می رسد.
7 حمیده با خود فکر می کرد که اگر چند بردار با هم جمع شوند، بردار حاصل جمع از همهٔ آنها بزرگ تر است. آیا او درست فکر کرده است؟ با کشیدن شکل توضیح دهید.
خیر، اشتباه فکر می کند؛ زیرا برآیند این چند بردار، برداری است که ابتدای آن، ابتدای اولین بردار و انتهای آن، انتهای آخرین بردار است؛ برای مثال:
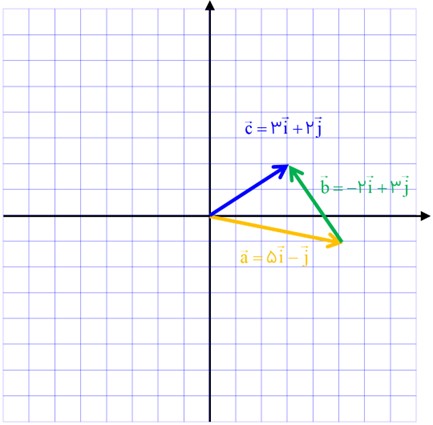
\(\begin{array}{l}\left\{ \begin{array}{l}\vec a = 5\vec i - \vec j\\\\\vec b = - 2\vec i + 3\vec j\end{array} \right.\\\\\vec a + \vec b = \vec c\\\\ \Rightarrow \vec c = 3\vec i + 2\vec j\end{array}\)
طبق پیشنهاد حمیده، بردار برآیند بایستی بزرگتر از دو بردار دیگر باشد، اما چنین نیست.
8 در صفحهٔ شطرنجی زیر، یک خودرو با نقطهٔ A مشخص شده است. این خودرو مسیری را طی کرده است تا به نقطهٔ B برسد؛ در کل به اندازهٔ چند واحد حرکت کرده است؟
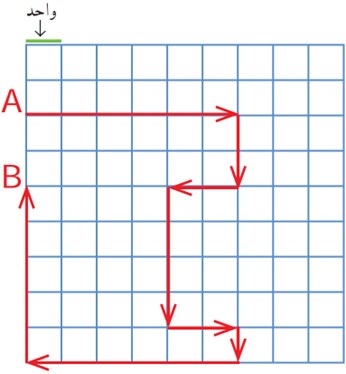
خودرو از نقطهٔ A به B در راستای عمودی چند واحد جا به جا شده است؟
در کل 28 واحد حرکت کرده است:
\(6 + 2 + 2 + 4 + 2 + 1 + 6 + 5 = 28\)واحد
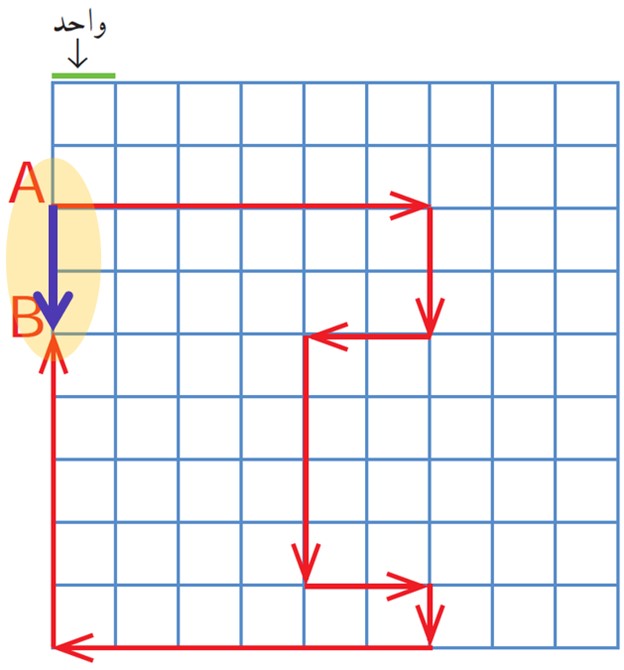
خودرو 2 واحد جا به جا شده است.
1736019749.png)
