جواب تمرین صفحه 67 درس 4 ریاضی هشتم (جبر و معادله)

\(\begin{array}{l} - \frac{3}{8}x + 5 = \frac{1}{6}\\\\\mathop \Rightarrow \limits^{ \times 24} \,\,\,\,\, - 9x + 120 = 4\\\\ \Rightarrow \,\,\,\,\, - 9x = 4 - 120 = - 116\\\\ \Rightarrow \,\,\,\,\,x = \frac{{ - 116}}{{ - 9}} = \frac{{116}}{9}\end{array}\)

\(\begin{array}{l}\frac{5}{{12}}x - \frac{7}{{18}} = 2\\\\\mathop \Rightarrow \limits^{ \times 36} \,\,\,\,\,15x - 14 = 72\\\\ \Rightarrow \,\,\,\,\,15x = 60 + 14 = 86\\\\ \Rightarrow \,\,\,\,\,x = \frac{{86}}{{15}}\end{array}\)

\(\begin{array}{l}4x + \frac{2}{7} = \frac{3}{2}x\\\\\mathop \Rightarrow \limits^{ \times 14} \,\,\,\,\,56x + 4 = 21x\\\\ \Rightarrow \,\,\,\,\,56x - 21x = - 4\\\\ \Rightarrow \,\,\,\,\,35x = - 4\\\\ \Rightarrow \,\,\,\,\,x = - \frac{4}{{35}}\end{array}\)

\(\begin{array}{l}2x - \frac{2}{3} = 5x + 3\\\\\mathop \Rightarrow \limits^{ \times 3} \,\,\,\,\,6x - 2 = 15x + 9\\\\ \Rightarrow \,\,\,\,\, - 2 - 9 = 15x - 6x\\\\ \Rightarrow \,\,\,\,\, - 11 = 9x\\\\ \Rightarrow \,\,\,\,\,x = - \frac{{11}}{9}\end{array}\)

\(\begin{array}{l}1 - \frac{{x + 1}}{2} = \frac{1}{3}\\\\\mathop \Rightarrow \limits^{ \times 6} \,\,\,\,\,6 - 3(x + 1) = 2\\\\ \Rightarrow \,\,\,\,\,6 - 3x - 3 = 2\\\\ \Rightarrow \,\,\,\,\,3 - 3x = 2\\\\ \Rightarrow \,\,\,\,\, - 3x = 2 - 3 = - 1\\\\ \Rightarrow \,\,\,\,\,x = \frac{{ - 1}}{{ - 3}} = \frac{1}{3}\end{array}\)

\(\begin{array}{l}\frac{1}{2} - \frac{{2x - 1}}{4} = \frac{3}{4}\\\\\mathop \Rightarrow \limits^{ \times 4} \,\,\,\,\,2 - (2x - 1) = 3\\\\ \Rightarrow \,\,\,\,\,2 - 2x + 1 = 3\\\\ \Rightarrow \,\,\,\,\, - 2x + 3 = 3\\\\ \Rightarrow \,\,\,\,\, - 2x = 3 - 3 = 0\\\\ \Rightarrow \,\,\,\,\,x = \frac{0}{{ - 2}} = 0\end{array}\)

\(\begin{array}{l}2(x + 5) = 24\\\\ \Rightarrow x + 5 = \frac{{24}}{2} = 12\\\\ \Rightarrow x = 12 - 5 = 7\end{array}\)

\(\begin{array}{l}7x + 4 = 58\\\\ \Rightarrow 7x = 58 - 4\\\\ \Rightarrow 7x = 54\\\\ \Rightarrow x = \frac{{54}}{7}\end{array}\)

\(\begin{array}{l}x + (x + 1) + (x + 2) = 27\\\\ \Rightarrow 3x + 3 = 27\\\\ \Rightarrow 3x = 27 - 3 = 24\\\\ \Rightarrow x = \frac{{24}}{3} = 8\end{array}\)

\(\begin{array}{l}5x - 3 = 17\\\\ \Rightarrow 5x = 17 + 3 = 20\\\\ \Rightarrow x = \frac{{20}}{5} = 4\end{array}\)

\(\begin{array}{l}{x^2} + x = 42\\\\x = 42 \Rightarrow {(42)^2} + 42 = 1806 \otimes \\\\x = 14 \Rightarrow {(14)^2} + 14 = 210 \otimes \\\\x = - 6 \Rightarrow {( - 6)^2} + ( - 6) = 30 \otimes \\\\x = - 7 \Rightarrow {( - 7)^2} + ( - 7) = 42\\\\x = - 5 \Rightarrow {( - 5)^2} + ( - 5) = 20 \otimes \end{array}\)

پاسخ صحیح گزینه د می باشد.

\(\begin{array}{l}45 + x = (x + 9) + (x + 14)\\\\ \Rightarrow 45 + x = 2x + 23\\\\ \Rightarrow 45 - 23 = 2x - x\\\\ \Rightarrow x = 22\end{array}\)

\(\begin{array}{l}\left\{ \begin{array}{l}W = 12\\\\F = 4\\\\d = ?\end{array} \right.\\\\12 = 4d\\\\ \Rightarrow d = \frac{{12}}{4} = 3\end{array}\)

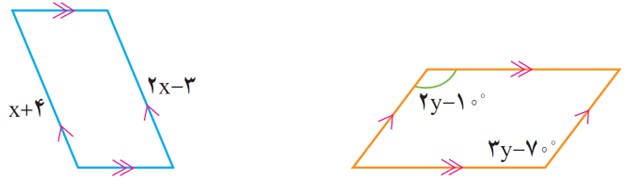
\(\begin{array}{l}x + 4 = 2x - 3\\\\ \Rightarrow 4 + 3 = 2x - x\\\\ \Rightarrow x = 7\end{array}\)

\(\begin{array}{l}2y - {10^ \circ } = 3y - {70^ \circ }\\\\ - {10^ \circ } + {70^ \circ } = 3y - 2y\\\\ \Rightarrow y = {60^ \circ }\end{array}\)