جواب فعالیت صفحه 62 درس 4 ریاضی هشتم (جبر و معادله)
تعداد بازدید : 86.33Mپاسخ فعالیت صفحه 62 ریاضی هشتم
-گام به گام فعالیت صفحه 62 درس جبر و معادله
-فعالیت صفحه 62 درس 4
-شما در حال مشاهده جواب فعالیت صفحه 62 ریاضی هشتم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 تفاوت \(2x\,,\,{x^2}\) چیست؟
\(\begin{array}{l}{x^2} = \\\\2x = \end{array}\)
\({x^2} = x \times x\)
در خودش ضرب شده است و اگر عددی صحیح باشد، ممکن است که مجذور آن یعنی \({x^2}\) هم زوج باشد و هم فرد.
\(2x = 2 \times x\)
x در عدد 2 ضرب شده است و اگر عددی صحیح باشد، عبارت 2x همواره زوج می باشد.
2 مانند نمونه، طرف دیگر تساوی ها را بنویسید.
\(\begin{array}{l}{3^2} = 3 \times 3\\\\{( - 5)^2} = \underline {\,\,\,\,\,\,\,} \times \underline {\,\,\,\,\,\,\,} \\\\{a^2} = \underline {\,\,\,\,\,\,\,} \times \underline {\,\,\,\,\,\,\,} \\\\{\bigcirc ^2} = \bigcirc \times \bigcirc \\\\{\Delta ^2} = \underline {\,\,\,\,\,\,\,} \times \underline {\,\,\,\,\,\,\,} \\\\{(a + b)^2} = \underline {\,\,\,\,\,\,\,} \times \underline {\,\,\,\,\,\,\,} \end{array}\)
\(\begin{array}{l}{( - 5)^2} = ( - 5) \times ( - 5)\\\\{a^2} = a \times a\\\\{\Delta ^2} = \Delta \times \Delta \\\\{(a + b)^2} = (a + b) \times (a + b)\end{array}\)
3 جدول زیر را برای مقدارهای مختلف a و b کامل کنید.
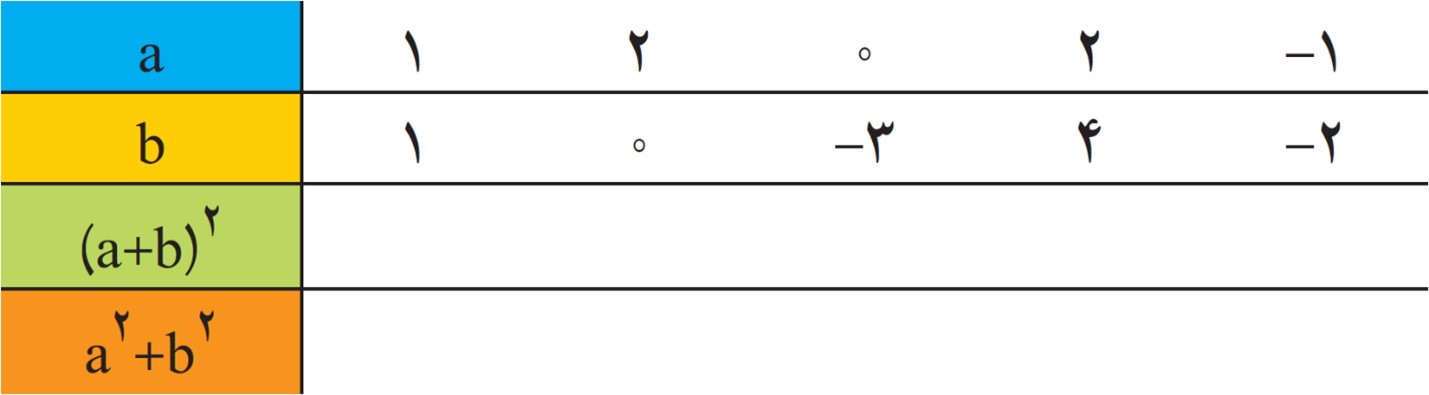
از مقایسهٔ دو ردیف آخر، چه نتیجه ای می گیرید؟
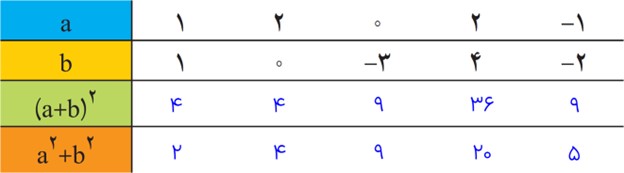
از مقایسۀ دو ردیف آخر نتیجه می گیریم که این دو عبارت ریاضی با هم مساوی نیستند؛ فقط به ازای اینکه یکی از مقادیر a یا b صفر باشد، این تساوی برقرار می شود؛ بنابراین داریم:
\({(a + b)^2} \ne {a^2} + {b^2}\)
4 مانند نمونه، عبارت ها را ساده کنید.
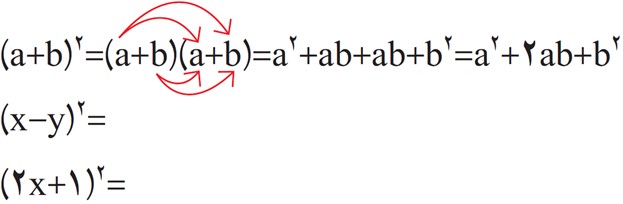
\(\begin{array}{l}{(x - y)^2} = (x - y) \times (x - y) = \\\\{x^2} - xy - xy + {y^2} = {x^2} - 2xy + {y^2}\end{array}\)
\(\begin{array}{l}{(2x + 1)^2} = (2x + 1) \times (2x + 1) = \\\\{(2x)^2} + (2x \times 1) + (1 \times 2x) + {1^2} = \\\\4{x^2} + 2x + 2x + 1 = 4{x^2} + 4x + 1\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















