شاه کلید نکات
شاه کلید سوال
1 با توجه به توابع f و g و h با ضابطه های داده شده، به سؤالات پاسخ دهید.
\(\begin{array}{l}f\left( x \right) = 2x + 1\\\\g\left( x \right) = 2x + 1\;\;\;x \ne 2\\\\h\left( x \right) = \left\{ \begin{array}{l}2 + x\;\;\;\;x \ne 2\\\\3\;\;\;\;\;\;\;\;x = 2\end{array} \right.\end{array}\)
الف مقادیر زیر را در صورت وجود به دست آورید:
f(2) =
g(2) =
h(2) =
ب حدود زیر را در صورت وجود به دست آورید:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 2} \;f\left( x \right) = \\\\\mathop {\lim }\limits_{x \to 2} \;g\left( x \right) = \\\\\mathop {\lim }\limits_{x \to 2} \;h\left( x \right) = \end{array}\)
پ کدام تابع در x = 2 پیوسته است؟
الف
f(2) = 2(2) + 1 = 5
g(2) = وجود ندارد
h(2) = 3
ب
\(\mathop {\lim }\limits_{x \to 2} \;f\left( x \right) = 5\)
\(\mathop {\lim }\limits_{x \to 2} \;g\left( x \right) = 5\)
\(\mathop {\lim }\limits_{x \to 2} \;h\left( x \right) = 5\)
پ تابع f ؛ زیرا حد تابع آن و مقدار تابع در آن نقطه باهم برابرند:
\(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = f\left( 2 \right) = 5\)
2 نمودار تابع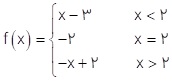 
را رسم کنید. f در چه نقاطی پیوسته و در چه نقاطی ناپیوسته است؟
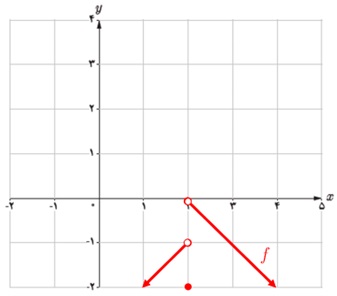
همان طور که در شکل مشاهده می کنیم تابع f فقط در نقطه 2 = x ناپیوسته است و در باقی نقاط پیوسته می باشد.
3 توابع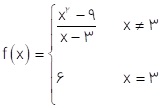 
و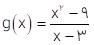 
را در نظر می گیریم. پیوستگی این تابع ها را در x = 3 بررسی کنید.
\(\begin{array}{l}f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}\frac{{{x^2} - 9}}{{x - 3}}\;\;\:,\;\;\:x \ne 3\\\end{array}\\{6\begin{array}{*{20}{c}}{}&{}\end{array}\;\;\:,\;\;\:x = 3}\end{array}} \right.\\\\\mathop {\lim }\limits_{x \to 3} f\left( x \right) = \mathop {\lim }\limits_{x \to 3} \frac{{{x^2} - 9}}{{x - 3}} = \\\\\mathop {\lim }\limits_{x \to 3} \frac{{\left( {x - 3} \right)\left( {x + 3} \right)}}{{\left( {x - 3} \right)}} = \\\\\mathop {\lim }\limits_{x \to 3} \left( {x + 3} \right) = 6\\\begin{array}{*{20}{l}}{}\\{f\left( 3 \right) = 6}\end{array}\\\\ \Rightarrow \mathop {\lim }\limits_{x \to 3} f\left( x \right) = f\left( 3 \right)\end{array}\)
تابع f در نقطه 2 = x پیوسته است
\(\begin{array}{l}g\left( x \right) = \frac{{{x^2} - 9}}{{x - 3}}\\\\\mathop {\lim }\limits_{x \to 3} g\left( x \right) = \mathop {\lim }\limits_{x \to 3} \frac{{{x^2} - 9}}{{x - 3}} = \\\\\mathop {\lim }\limits_{x \to 3} \frac{{\left( {x - 3} \right)\left( {x + 3} \right)}}{{\left( {x - 3} \right)}} = \\\\\mathop {\lim }\limits_{x \to 3} \left( {x + 3} \right) = 6\\\\g\left( 3 \right) = \not \exists \end{array}\)
تابع g در نقطه 2 = x ناپیوسته است
4 با توجه به نمودار تابع f(x) = [x] تابع در چه نقاطی پیوسته و در چه نقاطی ناپیوسته است؟
تابع f(x) = [x] فقط در نقاط به طول صحیح ناپیوسته است و پیوستگی از راست دارد و در نقاط دیگر پیوسته می باشد.
\(x \in \mathbb{Z} \Rightarrow f:\)ناپیوسته
پیوسته \(x \notin \mathbb{Z} \Rightarrow f:\)
5 پیوستگی تابع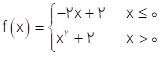 
را در نقطهٔ x = 0 بررسی کنید. پیوستگی تابع در نقاط دیگر چگونه است؟
\(\begin{array}{l}f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}\begin{array}{l} - 2x + 2\;\;\:,\;\;\:x \le 0\\\end{array}\\{{x^2} + 2\;\;\:\;\;\:,\;\;\:x > 0}\end{array}} \right.\\\\\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {{x^2} + 2} \right) = \\\\{\left( {{0^ + }} \right)^2} + 2 = 2\\\\\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( { - 2x + 2} \right) = \\\\ - 2\left( {{0^ - }} \right) + 2 = 2\\\\ \Rightarrow \mathop {\lim }\limits_{x \to 0} f\left( x \right) = 2\\\\f\left( 0 \right) = - 2\left( 0 \right) + 2 = 2\\\\ \Rightarrow \mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right)\end{array}\)
تابع f در نقطه 0 = x پیوسته است
تابع f در تمام نقاط دامنه اش پیوسته است:
\({x_0} \in \mathbb{R} \Rightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
6 تابعی مثال بزنید که حد آن در نقطهٔ x = 1 مساوی 1- باشد؛ ولی تابع در 1 پیوسته نباشد. نمودار این تابع را رسم کنید.
\(\begin{array}{l}f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}\begin{array}{l} - x\;\;\:,\;\;\:x \ne 1\\\end{array}\\{1\;\;\:\;\;\:,\;\;\:x = 1}\end{array}} \right.\\\\\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to 1} f\left( x \right) = - 1\\\\f\left( 1 \right) = 1\end{array} \right.\\\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} f\left( x \right) \ne f\left( 1 \right)\end{array}\)
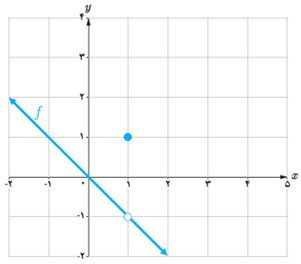
7 کدام یک از توابع زیر در x = 1 پیوسته است؟
تابع f در 1 = x پیوسته است:
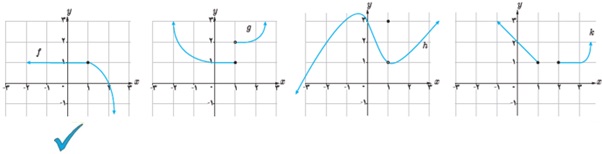
8 در مواقعی تجویز دارو برای کودکان بر اساس جرم کودک انجام می گیرد. روش های مختلفی برای برآورد کردن جرم یک کودک (برحسب کیلوگرم) در شرایط اضطراری (که جرم نمی تواند اندازه گیری شود) وجود دارد. یکی از این روش ها استفاده از تابع 
است که در آن سن کودک برحسب سال است. به طور مثال جرم یک کودک 6 ماهه به کمک این تابع چنین محاسبه می شود:
سال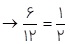 
6 ماه
\(f\left( {\frac{1}{2}} \right) = 6 \times \left( {\frac{1}{2}} \right) + 4 = 7\)
الف f(2) و f(5) را بیابید.
ب آیا f در بازۀ [0 , 10] پیوسته است؟
الف
f(2) = 2(2) + 10 = 14
f(5) = 2(5) + 10 = 20
ب خیر؛ تابع f در 1 = x ناپیوسته است؛ زیرا تابع در این نقطه حد ندارد:
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = 2\left( 1 \right) + 10 = 12\\\end{array}\\{\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = 6\left( 1 \right) + 4 = 10}\end{array}} \right.\\\\ \Rightarrow \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right)\\\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} f\left( x \right) = \not \exists \end{array}\)
حد وجود ندارد
1736019749.png)
