جواب تمرین صفحه 28 درس 1 حسابان یازدهم (جبر و معادله)
تعداد بازدید : 84.72Mپاسخ تمرین صفحه 28 حسابان یازدهم
-گام به گام تمرین صفحه 28 درس جبر و معادله
-تمرین صفحه 28 درس 1
-شما در حال مشاهده جواب تمرین صفحه 28 حسابان یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 با استفاده از تعیین علامت، ضابطهٔ هریک از توابع زیر را بدون استفاده از نماد قدر مطلق بنویسید.
الف \(f\left( x \right) = x\left| x \right|\)
ب \(g\left( x \right) = \left| {{x^2} - 1} \right|\)
پ \(h\left( x \right) = \left| {x - 1} \right| + \left| {x + 1} \right|\)
الف \(f\left( x \right) = x\left| x \right|\)
\(\left\{ \begin{array}{l}{x^2}\quad ,x \ge 0\\ - {x^2}\;,x < 0\end{array} \right.\)
ب \(g\left( x \right) = \left| {{x^2} - 1} \right|\)
\(\left\{ \begin{array}{l}{x^2} - 1\quad ,\left| x \right| \ge 1\\ - {x^2} + 1\;,\left| x \right| < 1\end{array} \right.\)
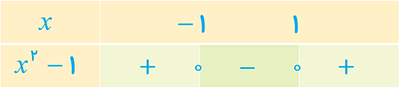
پ \(h\left( x \right) = \left| {x - 1} \right| + \left| {x + 1} \right|\)
\(\left\{ \begin{array}{l} - 2x\quad ,x < - 1\\2\begin{array}{*{20}{c}}{}&{}\end{array}\;, - 1 \le x < 1\\2x\quad \;\;\,,1 \le x\end{array} \right.\)
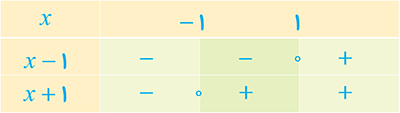
2 بر روی محور طول ها چه نقاطی وجود دارد که مجموع فاصله های آنها از دو نقطه به طول های 1- و 3 روی محور xها برابر 6 باشد؟
\(\begin{array}{l}\left| {x - \left( { - 1} \right)} \right| + \left| {x - 3} \right| = 6 \Rightarrow \left| {x + 1} \right| + \left| {x - 3} \right| = 6\\\left| {x + 1} \right| + \left| {x - 3} \right| = \left\{ \begin{array}{l} - 2x + 2\quad ,x < - 1\\4\begin{array}{*{20}{c}}{}&{}&{}\end{array}, - 1 \le x < 3\\2x - 2\quad \;\;\,,3 \le x\end{array} \right.\\\forall \left( {x < - 1} \right): - 2x + 2 = 6 \Rightarrow {x_1} = - 2\\\forall \left( {3 \le x} \right):\;\;\;2x - 2 = 6 \Rightarrow {x_2} = 4\end{array}\)
3 هر یک از عبارت های زیر را با استفاده از نماد قدر مطلق به صورت یک معادله یا نامعادله بنویسید و جواب را روی محور اعداد نمایش دهید.
الف فاصله بین x و 3 برابر 7 است
ب دو برابر فاصله بین x و 6 برابر 4 است.
پ فاصله بین x و 3- بزرگ تر از 2 است.
الف
\(\begin{array}{l}\left| {x - 3} \right| = 7 \Rightarrow x - 3 = \pm 7\\ \Rightarrow x = 3 \pm 7\\ \Rightarrow \left\{ \begin{array}{l}{x_1} = 3 + 7 = 10\\{x_2} = 3 - 7 = - 4\end{array} \right.\end{array}\)

ب
\(\begin{array}{l}2\left| {x - 6} \right| = 4 \Rightarrow \left| {x - 6} \right| = 2 \Rightarrow x - 6 = \pm 2\\ \Rightarrow x = 6 \pm 2\\ \Rightarrow \left\{ \begin{array}{l}{x_1} = 6 + 2 = 8\\{x_2} = 6 - 2 = 4\end{array} \right.\end{array}\)

پ
\(\begin{array}{l}\left| {x - \left( { - 3} \right)} \right| > 2 \Rightarrow \left| {x + 3} \right| > 2\\ \Rightarrow \left\{ \begin{array}{l}x + 3 > 2 \Rightarrow x > - 1\\x + 3 < - 2 \Rightarrow x < - 5\end{array} \right.\end{array}\)

4 دو معادلهٔ زیر را حل کنید.
الف \(\frac{{2 - x}}{{\left| {x - 3} \right|}} = 1\)
ب \(\sqrt {{x^2} - 2x + 1} = 2x + 1\)
الف
\(\begin{array}{l} \Rightarrow 2 - x = \left| {x - 3} \right|\;\mathop \Rightarrow \limits^{{{\left( {} \right)}^2}} \;\\{\left( {2 - x} \right)^2} = {\left| {x - 3} \right|^2} = {\left( {x - 3} \right)^2}\\ \Rightarrow 4 - 4x + {x^2} = {x^2} - 6x + 9\\ \Rightarrow 2x = 5 \Rightarrow x = \frac{5}{2}\end{array}\)
ب
\(\begin{array}{l}\;\mathop \Rightarrow \limits^{{{\left( {} \right)}^2}} \;{\left( {\sqrt {{x^2} - 2x + 1} } \right)^2} = {\left( {2x + 1} \right)^2}\\ \Rightarrow {x^2} - 2x + 1 = 4{x^2} + 4x + 1\\ \Rightarrow 3{x^2} + 6x = 0 \Rightarrow 3x\left( {x + 2} \right) = 0\\ \Rightarrow \left\{ \begin{array}{l}3x = 0 \Rightarrow {x_1} = 0\\x + 2 = 0 \Rightarrow {x_2} = - 2\;\; \otimes \\ \Rightarrow 3 = \sqrt {{{\left( { - 2} \right)}^2} - 2\left( { - 2} \right) + 1} \ne 2\left( { - 2} \right) + 1 = - 3\end{array} \right.\end{array}\)
5 نمودار هر یک از دو تابع زیر را رسم کنید، سپس به ازای y=3 معادله های به دست آمده را به روش هندسی و جبری حل کنید.
الف \(y = x - \frac{x}{{\left| {\,x\,} \right|}}\)
ب \(y = \left| {{x^2} - 6x} \right|\)
الف
\(\left\{ \begin{array}{l}x - 1\quad ,x > 0\\x + 1\quad ,x < 0\end{array} \right.\)
روش جبری :
\(\left\{ \begin{array}{l}\forall \left( {x > 0} \right):\quad x - 1 = 3 \Rightarrow x = 4\\\forall \left( {x < 0} \right):\quad x + 1 = 3 \Rightarrow x = 2\; \otimes \end{array} \right. \Rightarrow {x_ \circ } = 4\)
روش هندسی : \({x_ \circ } = 4\)
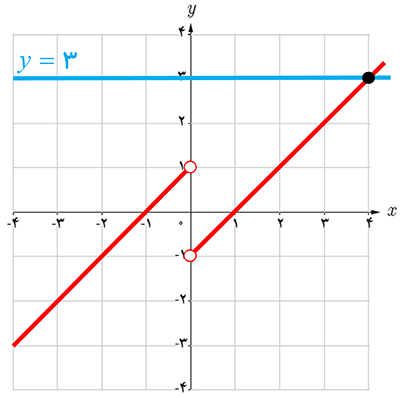
ب
\(\left\{ \begin{array}{l}{x^2} - 6x\quad \;\;,x < 0\\ - {x^2} + 6x\quad ,0 \le x < 6\\{x^2} - 6x\quad \;\;,6 \le x\end{array} \right.\)
روش جبری :
\(\begin{array}{l}\forall \left( {x < 0} \right) \cup \left( {6 \le x} \right):\quad {x^2} - 6x = 3 \Rightarrow \left\{ \begin{array}{l}{x_1} = 3 - 2\sqrt 3 \\{x_2} = 3 + 2\sqrt 3 \end{array} \right.\\\forall \left( {0 \le x < 6} \right):\quad - {x^2} + 6x = 3 \Rightarrow \left\{ \begin{array}{l}{x_3} = 3 - \sqrt 6 \\{x_4} = 3 + \sqrt 6 \end{array} \right.\end{array}\)
روش هندسی :
\(\left\{ \begin{array}{l}{x_1} = - 0/5\quad ,\quad {x_2} = 0/5\\{x_3} = 5/5\quad ,\quad {x_4} = 6/5\end{array} \right.\)
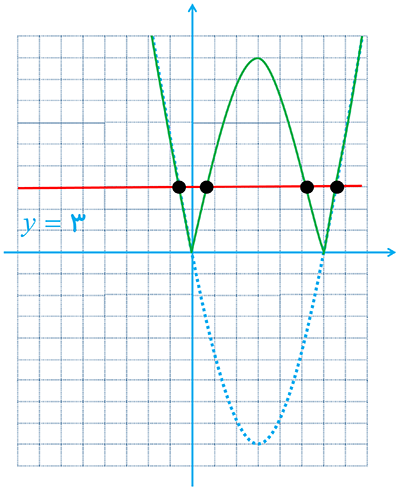
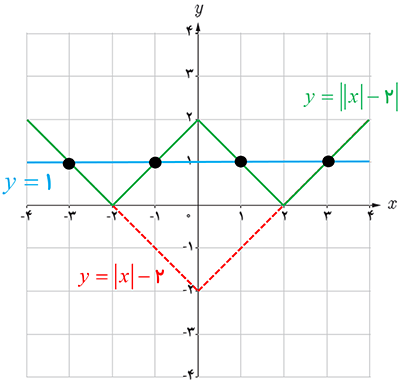
6 نمودار تابع f(x)=||x|-2| را رسم کنید، سپس معادله f(x)=1 را، هم به روش هندسی و هم به روش جبری، حل نمایید.
: روش جبری
\(\left| {\left| x \right| - 2} \right| = 1 \Rightarrow \left\{ \begin{array}{l}\left| x \right| - 2 = 1 \Rightarrow \left| x \right| = 3 \Rightarrow \left\{ \begin{array}{l}{x_1} = 3\\{x_2} = - 3\end{array} \right.\\\left| x \right| - 2 = - 1 \Rightarrow \left| x \right| = 1 \Rightarrow \left\{ \begin{array}{l}{x_3} = 1\\{x_4} = - 1\end{array} \right.\end{array} \right.\)
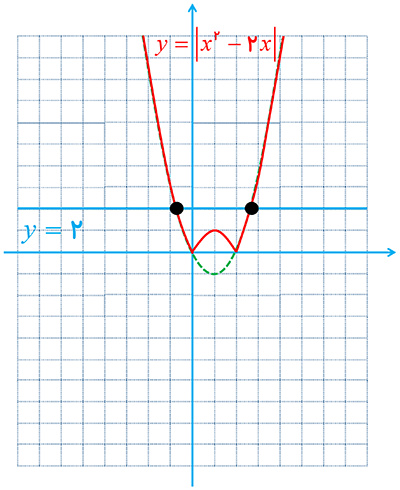
7 نمودار تابع \(f\left( x \right) = \left| {{x^2} - 2x} \right|\) را رسم کنید، سپس به دو روش هندسی و جبری معادله \(\left| {{x^2} - 2x} \right| = 2\) را حل نمایید.
: روش جبری
\(\begin{array}{l}\left| {{x^2} - 2x} \right| = 2\\\forall \left( {x < 0} \right) \cup \left( {2 \le x} \right):\quad {x^2} - 2x = 2 \Rightarrow \left\{ \begin{array}{l}{x_1} = 1 - \sqrt 3 \\{x_2} = 1 + \sqrt 3 \end{array} \right.\\\forall \left( {0 \le x < 2} \right):\quad - {x^2} + 2x = 2 \Rightarrow - {x^2} + 2x - 2 = 0\\\begin{array}{*{20}{c}}{}&{}&{}&{}&{}\end{array}\;\Delta = {\left( 2 \right)^2} - 4\left( { - 1} \right)\left( { - 2} \right) = - 4 < 0\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















