1736019749.png)
گام به گام فعالیت صفحه 27 درس 1 حسابان یازدهم (جبر و معادله)
تعداد بازدید : 64.41Mپاسخ فعالیت صفحه 27 حسابان یازدهم
-گام به گام فعالیت صفحه 27 درس جبر و معادله
-فعالیت صفحه 27 درس 1
-در شکل روبه رو نمودار تابعی با ضابطه \(f\left( x \right) = {x^2} - 4\) آمده است.
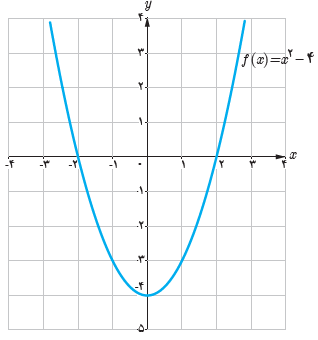
1 با توجه به علامت عبارت \({x^2} - 4\) و استفاده از تعریف قدر مطلق، تابع \(y = {x^2} - 4\) را به صورت چندضابطه ای بنویسید.
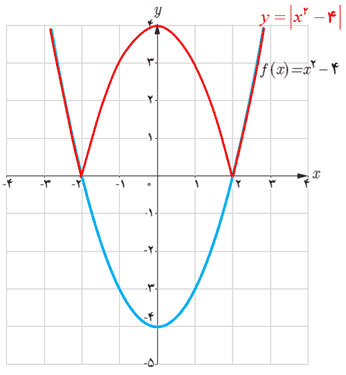
\(y = \left| {{x^2} - 4} \right| = \left\{ {\begin{array}{*{20}{l}}{{x^2} - 4\;\;\:,\left| x \right| > 2}\\{4 - {x^2}\;\;\:,\left| x \right| \le 2}\end{array}} \right.\)
2 نمودار \(y = \left| {{x^2} - 4} \right|\) را رسم کنید.
3 تابع y=|f(x)| را به صورت یک تابع دوضابطه ای بنویسید.
\(y = \left| {\,f(x)\,} \right| = \left\{ \begin{array}{l}\;\;\;\;\;\;\;,\;f\left( x \right) \ge 0\\\;\;\;\;\;\;\;,\;f\left( x \right) < 0\end{array} \right.\)
\(y = \left| {\,f(x)\,} \right| = \left\{ \begin{array}{l}f\left( x \right)\;\;\;\;\;,\;f\left( x \right) \ge 0\\ - f\left( x \right)\;\;\;,\;f\left( x \right) < 0\end{array} \right.\)
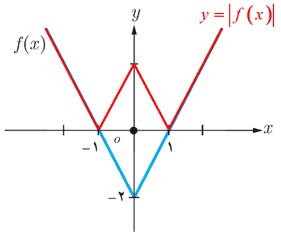
4 با توجه به قسمت های قبل یک روش رسم برای تابع y=|f(x)| از روی نمودار y=|f(x)| بیان کنید.
برای نقاطی که نمودار پایین محور طول ها است، قرینه آن ها را نسبت به محور x در بالای محور رسم می کنیم و نقاط بالای محور را بدون تأثیر باقی می گذاریم. سپس نقاط را به هم وصل می کنیم. در این صورت نمودار قدر مطلق تابع بدست می آید:
\(y = \left| {\,f(x)\,} \right| = \left\{ \begin{array}{l}f\left( x \right)\;\;\;\;\;,\;f\left( x \right) \ge 0\\ - f\left( x \right)\;\;\;,\;f\left( x \right) < 0\end{array} \right.\)
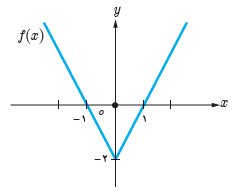
5 در شکل روبه رو نمودار تابع با ضابطه y=|f(x)| را از روی نمودار تابع y=f(x) رسم کنید.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
