جواب تمرین صفحه 35 درس 1 حسابان یازدهم (جبر و معادله)
تعداد بازدید : 84.72Mپاسخ تمرین صفحه 35 حسابان یازدهم
-گام به گام تمرین صفحه 35 درس جبر و معادله
-تمرین صفحه 35 درس 1
-شما در حال مشاهده جواب تمرین صفحه 35 حسابان یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
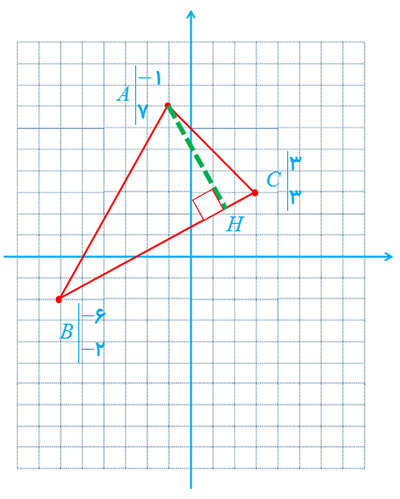
1 مثلث ABC به رأس های (7,1-)A و (2-,6-)B و (3,3)C را در نظر بگیرید.
الف مثلث را رسم کنید.
ب نشان دهید مثلث متساوی الساقین است.
پ معادله عمودمنصف ضلع BC را به دست آورید.
ت طول ارتفاع AH چقدر است؟
الف
برای رسم مثلث، ابتدا محورهای مختصات x و y را رسم میکنیم. سپس هر کدام از نقاط A، B و C را با توجه به طول (x) و عرض (y) آنها روی صفحه مشخص کرده و نقاط را به هم وصل میکنیم.
ب
برای اینکه نشان دهیم مثلث متساویالساقین است، باید طول اضلاع آن را محاسبه کنیم. اگر دو ضلع طول برابر داشته باشند، مثلث متساویالساقین است.
یادآوری: فرمول فاصله بین دو نقطه \((x_1, y_1)\) و \((x_2, y_2)\) برابر است با: \(d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\)
طول اضلاع AB و BC را محاسبه میکنیم:
\(\begin{array}{l}\left\{ \begin{array}{l}AB = \sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2}} \\BC = \sqrt {{{\left( {{x_B} - {x_C}} \right)}^2} + {{\left( {{y_B} - {y_C}} \right)}^2}} \end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}AB = \sqrt {{{\left( {\left( { - 1} \right) - \left( { - 6} \right)} \right)}^2} + {{\left( {7 - \left( { - 2} \right)} \right)}^2}} \\BC = \sqrt {{{\left( {\left( { - 6} \right) - 3} \right)}^2} + {{\left( {\left( { - 2} \right) - 3} \right)}^2}} \end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}AB = \sqrt {{5^2} + {9^2}} = \sqrt {25 + 81} = \sqrt {106} \\BC = \sqrt {{{\left( { - 9} \right)}^2} + {{\left( { - 5} \right)}^2}} = \sqrt {81 + 25} = \sqrt {106} \end{array} \right.\\\\ \Rightarrow AB = BC\end{array}\)
چون طول دو ضلع AB و BC برابر شد، مثلث ABC متساویالساقین است.
پ
عمودمنصف یک پارهخط، خطی است که از وسط آن پارهخط میگذرد و بر آن عمود است. برای یافتن معادله عمودمنصف ضلع BC، به دو چیز نیاز داریم:
- مختصات نقطه M، وسط پارهخط BC.
- شیب خط عمودمنصف که قرینه معکوس شیب خط BC است.
یادآوری:
- مختصات وسط پارهخط با نقاط انتهایی \((x_1, y_1)\) و \((x_2, y_2)\): \(M(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})\)
- شیب خط گذرا از دو نقطه \((x_1, y_1)\) و \((x_2, y_2)\): \(m = \frac{y_2-y_1}{x_2-x_1}\)
- معادله خط با شیب m و گذرنده از نقطه \((x_0, y_0)\): \(y - y_0 = m(x - x_0)\)
حواست باشه: اگر شیب یک خط m باشد، شیب خط عمود بر آن \(m' = -\frac{1}{m}\) است (به شرطی که m صفر نباشد).
ابتدا مختصات نقطه M (وسط BC) و سپس شیب خط BC و شیب خط عمودمنصف ('m) را محاسبه میکنیم:
\(\begin{array}{l}\left\{ \begin{array}{l}{x_M} = \frac{{{x_B} + {x_C}}}{2} = \frac{{\left( { - 6} \right) + 3}}{2} = \frac{{ - 3}}{2}\\{y_M} = \frac{{{y_B} + {y_C}}}{2} = \frac{{\left( { - 2} \right) + 3}}{2} = \frac{1}{2}\end{array} \right. \Rightarrow M\left( {\frac{{ - 3}}{2},\frac{1}{2}} \right)\\\\{m_{BC}} = \frac{{{y_B} - {y_C}}}{{{x_B} - {x_C}}} = \frac{{\left( { - 2} \right) - 3}}{{\left( { - 6} \right) - 3}} = \frac{{ - 5}}{{ - 9}} = \frac{5}{9}\\ \Rightarrow {{m'}} = \frac{{ - 1}}{{{m_{BC}}}} = \frac{{ - 1}}{{\frac{5}{9}}} = - \frac{9}{5}\end{array}\)
حالا معادله خط عمودمنصف را با استفاده از نقطه M و شیب 'm مینویسیم:
حواست باشه: محاسبات را با دقت انجام بده. اشتباه در یک عدد کل جواب را تغییر میدهد.
\(\begin{array}{l}y - {y_M} = {{m'}}\left( {x - {x_M}} \right)\\ \Rightarrow y - \frac{1}{2} = - \frac{9}{5}\left( {x - \left( { - \frac{3}{2}} \right)} \right)\\ \Rightarrow y - \frac{1}{2} = - \frac{9}{5}\left( {x + \frac{3}{2}} \right)\\ \Rightarrow y - \frac{1}{2} = - \frac{9}{5}x - \frac{{27}}{{10}}\\ \Rightarrow y = - \frac{9}{5}x - \frac{{27}}{{10}} + \frac{1}{2}\\ \Rightarrow y = - \frac{9}{5}x - \frac{{27}}{{10}} + \frac{5}{{10}}\\ \Rightarrow y = - \frac{9}{5}x - \frac{{22}}{{10}}\\ \Rightarrow y = - \frac{9}{5}x - \frac{{11}}{5}\end{array}\)
یا به صورت استاندارد: \(10y = -18x - 22 \Rightarrow 18x + 10y = -22 \Rightarrow 9x + 5y = -11\)
ت
ارتفاع AH، پارهخطی است که از راس A بر ضلع مقابل (BC) عمود میشود. طول ارتفاع AH برابر با فاصله نقطه A تا خط BC است.
یادآوری: فاصله نقطه \((x_0, y_0)\) از خط \(ax + by + c = 0\) برابر است با: \(d = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
ابتدا معادله خط BC را به فرم استاندارد \(ax + by + c = 0\) مینویسیم. از قسمت قبل شیب BC را 5/9 داریم:
\(\begin{array}{l}y - {y_C} = {m_{BC}}\left( {x - {x_C}} \right)\\ \Rightarrow y - 3 = \frac{5}{9}\left( {x - 3} \right)\\ \Rightarrow 9(y - 3) = 5(x - 3)\\ \Rightarrow 9y - 27 = 5x - 15\\ \Rightarrow 5x - 9y + 12 = 0\end{array}\)
حالا فاصله نقطه A(-1, 7) را از خط \(5x - 9y + 12 = 0\) محاسبه میکنیم:
\(\begin{array}{l}AH = \frac{{\left| {5{x_A} - 9{y_A} + 12} \right|}}{{\sqrt {{5^2} + {{\left( { - 9} \right)}^2}} }}\\ = \frac{{\left| {5\left( { - 1} \right) - 9\left( 7 \right) + 12} \right|}}{{\sqrt {25 + 81} }}\\ = \frac{{\left| { - 5 - 63 + 12} \right|}}{{\sqrt {106} }}\\ = \frac{{\left| { - 56} \right|}}{{\sqrt {106} }} = \frac{{56}}{{\sqrt {106} }}\\ = \frac{{56\sqrt {106} }}{{106}} = \frac{{28\sqrt {106} }}{{53}}\end{array}\)
(توجه: استفاده از معادله \(-5x + 9y - 12 = 0\) نیز به همین جواب منجر میشود).
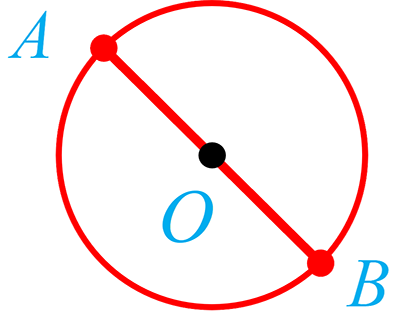
2 (6,0)A و (8-,8)B نقاط دوسر قطر یک دایره اند. مختصات مرکز و طول شعاع دایره را به دست آورید.
مرکز دایره (O) دقیقاً وسط قطر (AB) قرار دارد. شعاع دایره (R) نصف طول قطر (AB) است.
یادآوری:
- مختصات وسط پارهخط: \(M(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})\)
- فاصله بین دو نقطه (طول پارهخط): \(d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\)
ابتدا مختصات مرکز O را پیدا میکنیم:
\(\left\{ \begin{array}{l}{x_O} = \frac{{{x_A} + {x_B}}}{2} = \frac{{0 + 8}}{2} = 4\\{y_O} = \frac{{{y_A} + {y_B}}}{2} = \frac{{6 + \left( { - 8} \right)}}{2} = \frac{{ - 2}}{2} = - 1\end{array} \right. \Rightarrow O(4, -1)\)
سپس طول قطر AB را محاسبه میکنیم:
\(\begin{array}{l}AB = \sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2}} \\ = \sqrt {{{\left( {0 - 8} \right)}^2} + {{\left( {6 - \left( { - 8} \right)} \right)}^2}} \\ = \sqrt {{{\left( { - 8} \right)}^2} + {{\left( {14} \right)}^2}} = \sqrt{64 + 196} = \sqrt{260}\end{array}\)
نکته: برای سادهسازی رادیکال، میتوانیم عدد زیر رادیکال را تجزیه کنیم:
\(\sqrt{260} = \sqrt{4 \times 65} = \sqrt{4} \times \sqrt{65} = 2\sqrt{65}\)
در نهایت، شعاع R را به دست میآوریم:
\(R = \frac{{AB}}{2} = \frac{{2\sqrt {65} }}{2} = \sqrt {65}\)
پس مرکز دایره (4, -1) و شعاع آن \(\sqrt{65}\) است.
3 شکل نمای جانبی عدسی از منحنی سهمی به معادلهٔ \(y = {x^2} - 8x - 20\) مطابق شکل زیر مدل سازی می شود.
الف مختصات نقاط انتهای عدسی A و B را به دست آورید.
ب اگر x برحسب سانتی متر باشد طول AB را به دست آورید.
پ اگر عدسی کاملاً متقارن و y برحسب میلی متر باشد بیشترین ضخامت آن چقدر است؟
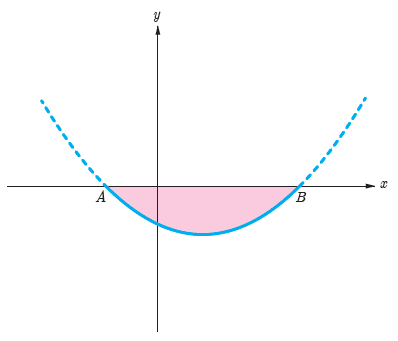
الف
نقاط انتهای عدسی (A و B) محل برخورد سهمی با محور xها هستند. در این نقاط، مقدار y برابر صفر است. پس باید معادله \(y = x^2 - 8x - 20 = 0\) را حل کنیم تا مقادیر x را پیدا کنیم.
یادآوری: برای حل معادله درجه دوم \(ax^2 + bx + c = 0\)، میتوان از فرمول \(x = \frac{{ - b \pm \sqrt \Delta }}{{2a}}\) استفاده کرد، که در آن \(\Delta = b^2 - 4ac\).
\(\begin{array}{l}{x^2} - 8x - 20 = 0\\ \Rightarrow \Delta = {b^2} - 4ac = {\left( { - 8} \right)^2} - 4\left( 1 \right)\left( { - 20} \right) = 64 + 80 = 144\\x = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{ - ( - 8) \pm \sqrt {144} }}{{2(1)}} = \frac{{8 \pm 12}}{2}\\ \Rightarrow \left\{ \begin{array}{l}{x_A} = \frac{{8 - 12}}{2} = \frac{{ - 4}}{2} = - 2 \Rightarrow A( - 2, 0)\\{x_B} = \frac{{8 + 12}}{2} = \frac{{20}}{2} = 10 \Rightarrow B(10, 0)\end{array} \right.\end{array}\)
ب
طول AB فاصله بین دو نقطه A و B است. چون هر دو نقطه روی محور xها هستند، طول AB برابر با قدر مطلق تفاضل xهای آنهاست.
\(AB = \left| {{x_B} - {x_A}} \right| = \left| {10 - ( - 2)} \right| = \left| {10 + 2} \right| = \left| {12} \right| = 12\;cm\)
پ
بیشترین ضخامت عدسی در این مدل، برابر با عمق سهمی است، یعنی فاصله عمودی از راس سهمی تا محور xها. راس سهمی نقطهای است که سهمی کمترین (یا بیشترین) مقدار y را دارد.
یادآوری: مختصات راس سهمی \(y = ax^2 + bx + c\) از \(x_S = \frac{-b}{2a}\) و \(y_S = f(x_S)\) به دست میآید.
ابتدا x راس سهمی را پیدا میکنیم:
\({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 8)}}{{2(1)}} = \frac{8}{2} = 4\)
سپس y راس سهمی (کمترین مقدار y) را محاسبه میکنیم:
حواست باشه: مقدار y در راس منفی است، اما ضخامت یک مقدار فیزیکی و مثبت است، پس باید قدر مطلق y راس را در نظر بگیریم.
\({y_{\min }} = f(x_S) = {(4)^2} - 8(4) - 20 = 16 - 32 - 20 = - 36\)
بیشترین ضخامت عدسی برابر با قدر مطلق \(y_{\min}\) است. چون y بر حسب میلیمتر است:
\({D_{\max }} = \left| {{y_{\min }}} \right| = \left| { - 36} \right| = 36\;mm\)
4 ثابت کنید فاصلهٔ دو خط موازی ax+by+c=0 و ax+by+c’=0 برابر \(\frac{{|c - c'|}}{{\sqrt {{a^2} + {b^2}} }}\) می باشد.
برای پیدا کردن فاصله بین دو خط موازی، کافی است یک نقطه دلخواه روی یکی از خطها انتخاب کنیم و سپس فاصله آن نقطه تا خط دیگر را محاسبه کنیم. این فاصله، همان فاصله بین دو خط موازی است.
نکته: این فرمول فقط زمانی معتبر است که ضریب x و y در هر دو معادله خط (a و b) یکسان باشند. اگر یکسان نبودند، ابتدا باید با ضرب یا تقسیم یک معادله، ضرایب را یکسان کنیم.
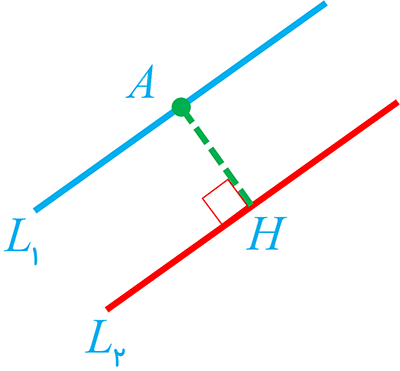
فرض کنیم \(L_1: ax + by + c = 0\) و \(L_2: ax + by + c' = 0\) دو خط موازی باشند.
نقطه \(A(x_A, y_A)\) را روی خط \(L_1\) در نظر میگیریم. پس مختصات این نقطه در معادله \(L_1\) صدق میکند:
\(a{x_A} + b{y_A} + c = 0 \Rightarrow a{x_A} + b{y_A} = - c\)
حالا فاصله نقطه A از خط \(L_2\) را با استفاده از فرمول فاصله نقطه از خط محاسبه میکنیم. این فاصله (AH) همان فاصله بین دو خط است.
یادآوری: فاصله نقطه \((x_0, y_0)\) از خط \(ax + by + c = 0\) برابر است با: \(d = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
\(\begin{array}{l}AH = \frac{{\left| {a{x_A} + b{y_A} + c'} \right|}}{{\sqrt {{a^2} + {b^2}} }}\end{array}\)
از رابطهای که برای نقطه A به دست آوردیم (\(a{x_A} + b{y_A} = - c\))، در فرمول بالا جایگذاری میکنیم:
\(\begin{array}{l}AH = \frac{{\left| {( - c) + c'} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \frac{{\left| {c' - c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\end{array}\)
چون \(|c' - c| = |c - c'|\)، پس فاصله دو خط برابر \(\frac{{\left| {c - c'} \right|}}{{\sqrt {{a^2} + {b^2}} }}\) است.
5 خط 4x+3y=5 بر دایرۀ C به مرکز (2,1-)O مماس است. طول شعاع دایره چقدر است؟
وقتی یک خط بر دایره مماس است، فاصله مرکز دایره تا آن خط دقیقاً برابر با شعاع دایره است.
یادآوری: فاصله نقطه \((x_0, y_0)\) از خط \(ax + by + c = 0\) برابر است با: \(d = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
ابتدا معادله خط را به فرم استاندارد \(ax + by + c = 0\) مینویسیم:
\(4x + 3y = 5 \Rightarrow 4x + 3y - 5 = 0\)
حالا فاصله مرکز O(-1, 2) را از این خط محاسبه میکنیم که همان شعاع (R) است:
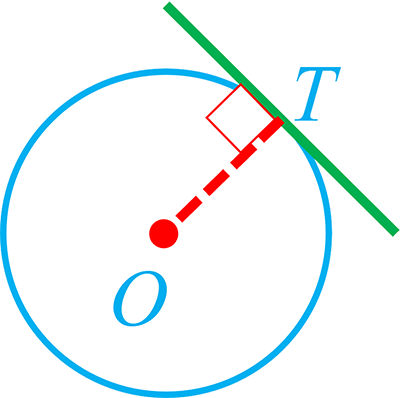
\(R = OT = \frac{{\left| {4{x_O} + 3{y_O} - 5} \right|}}{{\sqrt {{4^2} + {3^2}} }} = \frac{{\left| {4\left( { - 1} \right) + 3\left( 2 \right) - 5} \right|}}{{\sqrt {16 + 9} }} = \frac{{\left| { - 4 + 6 - 5} \right|}}{{\sqrt {25} }} = \frac{{\left| { - 3} \right|}}{5} = \frac{3}{5}\)
بنابراین، طول شعاع دایره برابر 3/5 است.
6 نقطۀ (8،x)S روی نیم دایره ای به شعاع 10 در شکل روبه رو داده شده است.
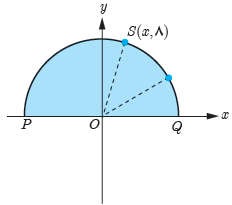
الف مقدار x را به دست آورید.
ب شیب خط های PS و SQ را به دست آورید.
پ نشان دهید زاویه PSQ قائمه است.
الف
نقطه S روی نیمدایرهای به مرکز مبدأ (0,0) و شعاع 10 قرار دارد. پس فاصله نقطه S تا مبدأ برابر 10 است. از طرفی، مختصات S به صورت (x, 8) داده شده است.
یادآوری: معادله دایره به مرکز مبدأ و شعاع R برابر \(x^2 + y^2 = R^2\) است. همچنین فاصله نقطه \((x, y)\) تا مبدأ برابر \(\sqrt{x^2 + y^2}\) است.
با استفاده از فرمول فاصله یا معادله دایره:
\(\begin{array}{l}OS = R = 10\\OS = \sqrt {{x_S}^2 + {y_S}^2} = \sqrt {{x^2} + {8^2}} \\ \Rightarrow \sqrt {{x^2} + 64} = 10\end{array}\)
برای حل، طرفین را به توان 2 میرسانیم:
\({x^2} + 64 = {10^2} = 100 \Rightarrow {x^2} = 100 - 64 = 36\\ \Rightarrow x = \pm \sqrt {36} = \pm 6\)
حواست باشه: با توجه به شکل، نقطه S در ربع اول قرار دارد، بنابراین مقدار x باید مثبت باشد. پس x = 6 قابل قبول است.
بنابراین مختصات نقطه S برابر (6, 8) است.
ب
نقاط P و Q دوسر قطر روی محور xها هستند و چون شعاع 10 است، مختصات آنها P(-10, 0) و Q(10, 0) است. نقطه S هم (6, 8) است. حالا شیب خطوط PS و SQ را محاسبه میکنیم.
یادآوری: شیب خط گذرا از \((x_1, y_1)\) و \((x_2, y_2)\): \(m = \frac{y_2-y_1}{x_2-x_1}\)
\(\begin{array}{l}S(6,8),\;P( - 10,0),\;Q(10,0)\\\\{m_{PS}} = \frac{{{y_S} - {y_P}}}{{{x_S} - {x_P}}} = \frac{{8 - 0}}{{6 - ( - 10)}} = \frac{8}{{6 + 10}} = \frac{8}{{16}} = \frac{1}{2}\\\\{m_{SQ}} = \frac{{{y_S} - {y_Q}}}{{{x_S} - {x_Q}}} = \frac{{8 - 0}}{{6 - 10}} = \frac{8}{{ - 4}} = - 2\end{array}\)
پ
برای اینکه نشان دهیم زاویه PSQ قائمه (90 درجه) است، باید ثابت کنیم خطوط PS و SQ بر هم عمودند. دو خط بر هم عمودند اگر حاصلضرب شیبهایشان برابر 1- باشد.
نکته: زاویه محاطی روبرو به قطر دایره همیشه قائمه است. چون S روی دایره و PQ قطر است، زاویه PSQ باید قائمه باشد. این روش اثبات هندسی آن است.
بررسی شرط عمود بودن با استفاده از شیبها:
\({m_{PS}} \times {m_{SQ}} = \left( {\frac{1}{2}} \right) \times \left( { - 2} \right) = - 1\)
چون حاصلضرب شیبها 1- شد، پس خطوط PS و SQ بر هم عمودند و زاویه \(P\hat{S}Q = 90^\circ\) است.
7 اگر فاصله نقطه (2,1)A از خط ax+4y=1 برابر 2 باشد، مقدار a چقدر است؟
از فرمول فاصله نقطه از خط استفاده میکنیم و مقدار فاصله را برابر 2 قرار میدهیم تا مقدار مجهول a را پیدا کنیم.
یادآوری: فاصله نقطه \((x_0, y_0)\) از خط \(Ax + By + C = 0\) برابر است با: \(d = \frac{{\left| {A{x_0} + B{y_0} + C} \right|}}{{\sqrt {{A^2} + {B^2}} }}\)
ابتدا معادله خط را به فرم استاندارد مینویسیم: \(ax + 4y - 1 = 0\). نقطه مورد نظر A(1, 2) و فاصله d=2 است.
\(\begin{array}{l}d = \frac{{\left| {a{x_A} + 4{y_A} - 1} \right|}}{{\sqrt {{a^2} + {4^2}} }} = 2\\ \Rightarrow \frac{{\left| {a\left( 1 \right) + 4\left( 2 \right) - 1} \right|}}{{\sqrt {{a^2} + 16} }} = 2\\ \Rightarrow \frac{{\left| {a + 8 - 1} \right|}}{{\sqrt {{a^2} + 16} }} = 2\\ \Rightarrow \frac{{\left| {a + 7} \right|}}{{\sqrt {{a^2} + 16} }} = 2\\ \Rightarrow \left| {a + 7} \right| = 2\sqrt {{a^2} + 16} \end{array}\)
برای حل این معادله قدر مطلقی، طرفین را به توان 2 میرسانیم:
حواست باشه: هنگام به توان رساندن طرفین یک تساوی، ممکن است جوابهای اضافی ایجاد شود. البته در این مورد چون هر دو طرف نامنفی هستند (قدر مطلق و رادیکال با ضریب مثبت)، مشکلی پیش نمیآید.
\(\begin{array}{l}{\left( {\left| {a + 7} \right|} \right)^2} = {\left( {2\sqrt {{a^2} + 16} } \right)^2}\\ \Rightarrow {\left( {a + 7} \right)^2} = 4\left( {{a^2} + 16} \right)\\ \Rightarrow {a^2} + 14a + 49 = 4{a^2} + 64\\ \Rightarrow 0 = (4{a^2} - {a^2}) - 14a + (64 - 49)\\ \Rightarrow 3{a^2} - 14a + 15 = 0\end{array}\)
این یک معادله درجه دوم است که با استفاده از فرمول دلتا حل میکنیم:
\(\begin{array}{l}\Delta = {b^2} - 4ac = {\left( { - 14} \right)^2} - 4\left( 3 \right)\left( {15} \right) = 196 - 180 = 16\\a = \frac{{ - b \pm \sqrt \Delta }}{{2a'}} = \frac{{ - ( - 14) \pm \sqrt {16} }}{{2(3)}} = \frac{{14 \pm 4}}{6}\\ \Rightarrow \left\{ \begin{array}{l}{a_1} = \frac{{14 + 4}}{6} = \frac{{18}}{6} = 3\\{a_2} = \frac{{14 - 4}}{6} = \frac{{10}}{6} = \frac{5}{3}\end{array} \right.\end{array}\)
بنابراین مقادیر ممکن برای a برابر 3 و 5/3 هستند.
8 سه رأس مثلث ABC ، (13-,11-)A ، (3,3-)B و (1,3)C می باشند.
الف طول عمودی را که از رأس B بر میانه نظیر رأس C وارد می شود به دست آورید.
ب مختصات رأس D را چنان تعیین کنید که ABCD یک متوازی الاضلاع باشد.
الف
میانه نظیر راس C، پارهخطی است که راس C را به وسط ضلع مقابلش (یعنی AB) وصل میکند. فرض کنیم M وسط AB باشد. میانه نظیر راس C همان خط CM است. ما میخواهیم طول عمود وارد شده از راس B بر خط CM را پیدا کنیم. این طول برابر است با فاصله نقطه B از خط CM.
مراحل حل:
- یافتن مختصات نقطه M (وسط AB).
- یافتن معادله خط CM.
- محاسبه فاصله نقطه B از خط CM.
یادآوری: فرمولهای لازم: مختصات نقطه وسط، شیب خط، معادله خط، فاصله نقطه از خط.
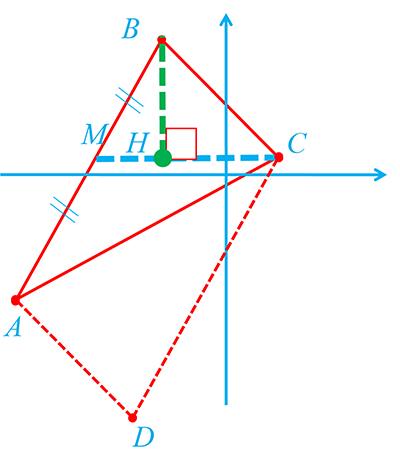
1. محاسبه مختصات M:
\(\left\{ \begin{array}{l}{x_M} = \frac{{{x_A} + {x_B}}}{2} = \frac{{\left( { - 11} \right) + \left( { - 3} \right)}}{2} = \frac{{ - 14}}{2} = - 7\\{y_M} = \frac{{{y_A} + {y_B}}}{2} = \frac{{\left( { - 13} \right) + 3}}{2} = \frac{{ - 10}}{2} = - 5\end{array} \right. \Rightarrow M( - 7, - 5)\)
2. محاسبه معادله خط CM (گذرنده از C(3,1) و M(-7,-5)):
\(\begin{array}{l}{m_{CM}} = \frac{{{y_C} - {y_M}}}{{{x_C} - {x_M}}} = \frac{{1 - \left( { - 5} \right)}}{{3 - \left( { - 7} \right)}} = \frac{{1 + 5}}{{3 + 7}} = \frac{6}{{10}} = \frac{3}{5}\\ \Rightarrow {L_{CM}}:y - {y_C} = {m_{CM}}\left( {x - {x_C}} \right)\\ \Rightarrow y - 1 = \frac{3}{5}\left( {x - 3} \right)\\ \Rightarrow 5(y - 1) = 3(x - 3)\\ \Rightarrow 5y - 5 = 3x - 9\\ \Rightarrow 3x - 5y - 4 = 0\end{array}\)
3. محاسبه فاصله نقطه B(-3, 3) از خط \(3x - 5y - 4 = 0\) (طول BH):
\(\begin{array}{l}BH = \frac{{\left| {3{x_B} - 5{y_B} - 4} \right|}}{{\sqrt {{3^2} + {{\left( { - 5} \right)}^2}} }}\\ = \frac{{\left| {3\left( { - 3} \right) - 5\left( 3 \right) - 4} \right|}}{{\sqrt {9 + 25} }}\\ = \frac{{\left| { - 9 - 15 - 4} \right|}}{{\sqrt {34} }} = \frac{{\left| { - 28} \right|}}{{\sqrt {34} }} = \frac{{28}}{{\sqrt {34} }}\\ = \frac{{28\sqrt {34} }}{{34}} = \frac{{14\sqrt {34} }}{{17}}\end{array}\)
(توجه: استفاده از معادله \(-3x + 5y + 4 = 0\) نیز به همین جواب منجر میشود).
ب
در متوازیالاضلاع ABCD، اضلاع روبهرو موازی و مساوی هستند. برای یافتن راس D، میتوانیم از موازی بودن اضلاع استفاده کنیم: خط AD موازی با BC است و خط CD موازی با AB است. نقطه D محل تلاقی این دو خط خواهد بود.
مراحل حل:
- محاسبه شیب BC (\(m_{BC}\)).
- نوشتن معادله خط AD (گذرا از A با شیب \(m_{BC}\)).
- محاسبه شیب AB (\(m_{AB}\)).
- نوشتن معادله خط CD (گذرا از C با شیب \(m_{AB}\)).
- حل دستگاه معادلات خطوط AD و CD برای یافتن مختصات D.
نکته (روش سریعتر): در متوازیالاضلاع، قطرها یکدیگر را نصف میکنند. یعنی نقطه وسط قطر AC همان نقطه وسط قطر BD است. با فرض D(x, y)، میتوان نوشت:
\((\frac{x_A+x_C}{2}, \frac{y_A+y_C}{2}) = (\frac{x_B+x_D}{2}, \frac{y_B+y_D}{2})\)
\((\frac{-11+3}{2}, \frac{-13+1}{2}) = (\frac{-3+x}{2}, \frac{3+y}{2})\)
\((\frac{-8}{2}, \frac{-12}{2}) = (\frac{-3+x}{2}, \frac{3+y}{2})\)
\(-4 = \frac{-3+x}{2} \Rightarrow -8 = -3+x \Rightarrow x = -5\)
\(-6 = \frac{3+y}{2} \Rightarrow -12 = 3+y \Rightarrow y = -15\)
پس D(-5, -15). این روش معمولا محاسبات کمتری دارد.
محاسبات با روش اول (تقاطع خطوط):
\(\begin{array}{l}{m_{BC}} = \frac{{{y_B} - {y_C}}}{{{x_B} - {x_C}}} = \frac{{3 - 1}}{{\left( { - 3} \right) - 3}} = \frac{2}{{ - 6}} = - \frac{1}{3}\\ \Rightarrow {L_{AD}}:y - {y_A} = {m_{BC}}\left( {x - {x_A}} \right)\\ \Rightarrow y - ( - 13) = - \frac{1}{3}(x - ( - 11))\\ \Rightarrow y + 13 = - \frac{1}{3}(x + 11)\\ \Rightarrow 3(y + 13) = - (x + 11)\\ \Rightarrow 3y + 39 = - x - 11\\ \Rightarrow {L_{AD}}:x + 3y = - 50\\\\{m_{AB}} = \frac{{{y_A} - {y_B}}}{{{x_A} - {x_B}}} = \frac{{\left( { - 13} \right) - 3}}{{\left( { - 11} \right) - \left( { - 3} \right)}} = \frac{{ - 16}}{{ - 11 + 3}} = \frac{{ - 16}}{{ - 8}} = 2\\ \Rightarrow {L_{CD}}:y - {y_C} = {m_{AB}}\left( {x - {x_C}} \right)\\ \Rightarrow y - 1 = 2(x - 3)\\ \Rightarrow y - 1 = 2x - 6\\ \Rightarrow {L_{CD}}: - 2x + y = - 5\\\\\text{Solve the system:}\\\left\{ \begin{array}{l}x + 3y = - 50\\ - 2x + y = - 5\end{array} \right.\\\text{From second equation: } y = 2x - 5\\\text{Substitute into first: } x + 3(2x - 5) = - 50\\ \Rightarrow x + 6x - 15 = - 50\\ \Rightarrow 7x = - 35 \Rightarrow x = - 5\\\text{Substitute x back into y equation: } y = 2( - 5) - 5 = - 10 - 5 = - 15\\ \Rightarrow D( - 5, - 15)\end{array}\)
9 نقطه ای روی خط y=2x تعیین کنید که مجموع فاصله های آن تا مبدأ مختصات و نقطه (4,2)A برابر 5 باشد.
فرض کنیم نقطه مورد نظر B روی خط y=2x باشد. پس مختصات B را میتوان به صورت \((x_B, 2x_B)\) نوشت. ما میخواهیم نقطهای پیدا کنیم که مجموع فاصله آن تا مبدأ O(0,0) و تا نقطه A(4,2) برابر 5 باشد. یعنی: \(|OB| + |AB| = 5\)
حواست باشه: در متن سوال نقطه A(4,2) داده شده، اما راه حل ارائه شده بر اساس نقطه A(2,4) است. ما در اینجا راه حل را مطابق با محاسبات ارائه شده (یعنی با فرض A(2,4)) تکمیل میکنیم. اگر A(4,2) مدنظر بود، محاسبات فاصله AB متفاوت خواهد بود.
یادآوری: فاصله بین دو نقطه \((x_1, y_1)\) و \((x_2, y_2)\): \(d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\)
فاصلههای OB و AB را محاسبه میکنیم (با فرض A(2,4)):
\(\left\{ \begin{array}{l}|OB| = \sqrt{{(x_B - 0)^2 + (2x_B - 0)^2}} = \sqrt{x_B^2 + 4x_B^2} = \sqrt{5x_B^2} = \sqrt 5 |x_B|\\|AB| = \sqrt{{(x_B - 2)^2 + (2x_B - 4)^2}} = \sqrt{{(x_B - 2)^2 + (2(x_B - 2))^2}} \\= \sqrt{{(x_B - 2)^2 + 4(x_B - 2)^2}} = \sqrt{5(x_B - 2)^2} = \sqrt 5 |x_B - 2|\end{array} \right.\)
حالا معادله \(|OB| + |AB| = 5\) را بازنویسی میکنیم:
\(\begin{array}{l}\sqrt 5 |x_B| + \sqrt 5 |x_B - 2| = 5\\ \Rightarrow \sqrt 5 (|x_B| + |x_B - 2|) = 5\\ \Rightarrow |x_B| + |x_B - 2| = \frac{5}{{\sqrt 5 }} = \sqrt 5 \end{array}\)
برای حل این معادله قدر مطلقی، باید حالتهای مختلف را بر اساس ریشههای داخل قدر مطلق (0 و 2) بررسی کنیم:
حالت 1: \(x_B < 0\)
در این حالت \(|x_B| = -x_B\) و \(|x_B - 2| = -(x_B - 2) = 2 - x_B\).
\(\begin{array}{l}(-x_B) + (2 - x_B) = \sqrt 5 \\ \Rightarrow 2 - 2x_B = \sqrt 5 \\ \Rightarrow 2x_B = 2 - \sqrt 5 \\ \Rightarrow x_B = \frac{{2 - \sqrt 5 }}{2}\end{array}\)
چون \(\sqrt 5 \approx 2.23\)، مقدار \(x_B\) منفی است و در شرط \(x_B < 0\) صدق میکند. پس این یک جواب است.
\({y_B} = 2{x_B} = 2\left( {\frac{{2 - \sqrt 5 }}{2}} \right) = 2 - \sqrt 5\). نقطه اول: \(B_1\left( {\frac{{2 - \sqrt 5 }}{2},2 - \sqrt 5 } \right)\)
حالت 2: \(0 \le x_B < 2\)
در این حالت \(|x_B| = x_B\) و \(|x_B - 2| = -(x_B - 2) = 2 - x_B\).
\(\begin{array}{l}(x_B) + (2 - x_B) = \sqrt 5 \\ \Rightarrow 2 = \sqrt 5 \end{array}\)
این تساوی نادرست است، پس در این بازه جوابی وجود ندارد.
حالت 3: \(x_B \ge 2\)
در این حالت \(|x_B| = x_B\) و \(|x_B - 2| = x_B - 2\).
\(\begin{array}{l}(x_B) + (x_B - 2) = \sqrt 5 \\ \Rightarrow 2x_B - 2 = \sqrt 5 \\ \Rightarrow 2x_B = 2 + \sqrt 5 \\ \Rightarrow x_B = \frac{{2 + \sqrt 5 }}{2}\end{array}\)
چون \(\sqrt 5 \approx 2.23\)، مقدار \(x_B \approx 2.115\) که بزرگتر یا مساوی 2 است و در شرط \(x_B \ge 2\) صدق میکند. پس این هم یک جواب است.
\({y_B} = 2{x_B} = 2\left( {\frac{{2 + \sqrt 5 }}{2}} \right) = 2 + \sqrt 5\). نقطه دوم: \(B_2\left( {\frac{{2 + \sqrt 5 }}{2},2 + \sqrt 5 } \right)\)
بنابراین دو نقطه با این ویژگی وجود دارد.
10 نقاط (2,4)A و (1-,1)B و (2-,8)C سه رأس مثلث ABC هستند. اگر H و M به ترتیب پای ارتفاع AH و میانه AM باشند طول MH را به دست آورید.
در این سوال باید فاصله بین پای میانه AM و پای ارتفاع AH را پیدا کنیم.
مراحل حل:
- یافتن مختصات M (وسط BC).
- یافتن معادله خط BC.
- یافتن معادله خط ارتفاع AH (خط گذرا از A و عمود بر BC).
- یافتن مختصات H (محل تلاقی دو خط BC و AH).
- محاسبه فاصله بین دو نقطه M و H.
حواست باشه: محاسبات این سوال کمی طولانی است و احتمال خطا وجود دارد. مراحل را با دقت دنبال کن.
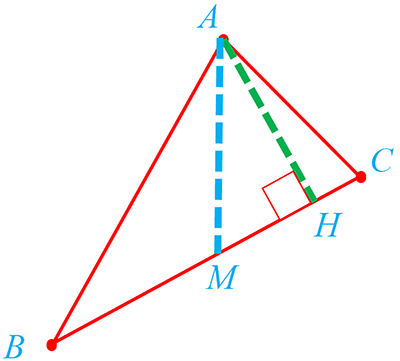
1. محاسبه مختصات M:
\(\left\{ \begin{array}{l}{x_M} = \frac{{{x_B} + {x_C}}}{2} = \frac{{1 + 8}}{2} = \frac{9}{2}\\{y_M} = \frac{{{y_B} + {y_C}}}{2} = \frac{{\left( { - 1} \right) + \left( { - 2} \right)}}{2} = - \frac{3}{2}\end{array} \right. \Rightarrow M\left( {\frac{9}{2}, - \frac{3}{2}} \right)\)
2. محاسبه معادله خط BC (گذرنده از B(1,-1) و C(8,-2)):
\(\begin{array}{l}{m_{BC}} = \frac{{{y_B} - {y_C}}}{{{x_B} - {x_C}}} = \frac{{\left( { - 1} \right) - \left( { - 2} \right)}}{{1 - 8}} = \frac{{ - 1 + 2}}{{ - 7}} = - \frac{1}{7}\\ \Rightarrow y - {y_B} = {m_{BC}}\left( {x - {x_B}} \right)\\ \Rightarrow y - (-1) = - \frac{1}{7}(x - 1)\\ \Rightarrow y + 1 = - \frac{1}{7}x + \frac{1}{7}\\ \Rightarrow 7(y + 1) = - x + 1\\ \Rightarrow 7y + 7 = - x + 1\\ \Rightarrow {L_{BC}}: x + 7y = -6\end{array}\)
3. محاسبه معادله خط ارتفاع AH (گذرا از A(4,2) و عمود بر BC):
شیب خط AH قرینه معکوس شیب BC است:
\({m_{AH}} = \frac{{ - 1}}{{{m_{BC}}}} = \frac{{ - 1}}{{ - 1/7}} = 7\)
معادله خط AH:
\(\begin{array}{l}y - {y_A} = {m_{AH}}\left( {x - {x_A}} \right)\\ \Rightarrow y - 2 = 7(x - 4)\\ \Rightarrow y - 2 = 7x - 28\\ \Rightarrow {L_{AH}}: - 7x + y = - 26\end{array}\)
4. یافتن مختصات H (حل دستگاه معادلات خطوط BC و AH):
\(\left\{ \begin{array}{l}x + 7y = -6 \quad (\times 7) \\ - 7x + y = - 26\end{array} \right. \Rightarrow \left\{ \begin{array}{l}7x + 49y = -42\\ - 7x + y = - 26\end{array} \right.\)
با جمع دو معادله:
\((7x + 49y) + (-7x + y) = -42 + (-26)\\ \Rightarrow 50y = -68\\ \Rightarrow y_H = \frac{-68}{50} = -\frac{34}{25}\)
با جایگذاری y در معادله اول:
\(x + 7(-\frac{34}{25}) = -6\\ \Rightarrow x - \frac{238}{25} = -6\\ \Rightarrow x = -6 + \frac{238}{25} = \frac{-150 + 238}{25} = \frac{88}{25}\\ \Rightarrow x_H = \frac{88}{25}\)
پس مختصات H برابر \((\frac{88}{25}, -\frac{34}{25})\) است.
5. محاسبه فاصله MH:
\(M(\frac{9}{2}, -\frac{3}{2})\) و \(H(\frac{88}{25}, -\frac{34}{25})\)
\(\begin{array}{l}MH = \sqrt {{{\left( {{x_M} - {x_H}} \right)}^2} + {{\left( {{y_M} - {y_H}} \right)}^2}} \\ = \sqrt {{{\left( {\frac{9}{2} - \frac{88}{25}} \right)}^2} + {{\left( { - \frac{3}{2} - \left( { - \frac{34}{25}} \right)} \right)}^2}} \\ = \sqrt {{{\left( {\frac{{9 \times 25 - 88 \times 2}}{{50}}} \right)}^2} + {{\left( {\frac{{ - 3 \times 25 + 34 \times 2}}{{50}}} \right)}^2}} \\ = \sqrt {{{\left( {\frac{{225 - 176}}{{50}}} \right)}^2} + {{\left( {\frac{{ - 75 + 68}}{{50}}} \right)}^2}} \\ = \sqrt {{{\left( {\frac{{49}}{{50}}} \right)}^2} + {{\left( {\frac{{ - 7}}{{50}}} \right)}^2}} \\ = \sqrt {\frac{{{49^2}}}{{{{50}^2}}} + \frac{{{7^2}}}{{{{50}^2}}}} = \sqrt {\frac{{2401 + 49}}{{{{50}^2}}}} \\ = \sqrt {\frac{{2450}}{{2500}}} = \sqrt {\frac{{245}}{{250}}} = \sqrt {\frac{{49 \times 5}}{{50 \times 5}}} = \sqrt {\frac{{49}}{{50}}} \\ = \frac{{\sqrt {49} }}{{\sqrt {50} }} = \frac{7}{{5\sqrt 2 }} = \frac{{7\sqrt 2 }}{{5 \times 2}} = \frac{{7\sqrt 2 }}{{10}}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















