جواب تمرین صفحه 83 درس 3 ریاضی و آمار دوازدهم انسانی (الگوهای غیر خطی)
تعداد بازدید : 84.72Mپاسخ تمرین صفحه 83 ریاضی و آمار دوازدهم انسانی
-گام به گام تمرین صفحه 83 درس الگوهای غیر خطی
-تمرین صفحه 83 درس 3
-شما در حال مشاهده جواب تمرین صفحه 83 ریاضی و آمار دوازدهم انسانی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 با نوشتن جملات رابطه های بازگشتی مشخص کنید کدام یک از آنها یک دنبالهٔ هندسی را تشکیل می دهد.
1 \({a_{n + 1}} = {\left( {{a_n}} \right)^2}\;\;\;\;{a_1} = \frac{1}{2}\)
2 \({a_{n + 1}} = \frac{2}{3}{a_n}\;\;\;\;{a_1} = \frac{1}{2}\)
3 \({a_{n + 1}} = \frac{1}{{1 + {a_n}}}\;\;\;\;{a_1} = 1\)
4 \({a_{n + 1}} = 2{a_n}\;\;\;\;{a_1} = 1\)
1 \({a_{n + 1}} = {\left( {{a_n}} \right)^2}\;\;\;\;{a_1} = \frac{1}{2}\)
\( \Rightarrow \;\;\:\frac{1}{2}\;\;\:,\;\;\:\frac{1}{4}\;\;\:,\;\;\:\frac{1}{{16}}\;\;\:,\;\;\: \cdots \)
2 \({a_{n + 1}} = \frac{2}{3}{a_n}\;\;\;\;{a_1} = \frac{1}{2}\)
\( \Rightarrow \;\;\:\frac{1}{2}\;\;\:,\;\;\:\frac{1}{3}\;\;\:,\;\;\:\frac{2}{9}\;\;\:,\;\;\: \cdots \)
دنباله هندسی
3 \({a_{n + 1}} = \frac{1}{{1 + {a_n}}}\;\;\;\;{a_1} = 1\)
\( \Rightarrow \;\;\:1\;\;\:,\;\;\:\frac{1}{2}\;\;\:,\;\;\:\frac{2}{3}\;\;\:,\;\;\: \cdots \)
4 \({a_{n + 1}} = 2{a_n}\;\;\;\;{a_1} = 1\)
\( \Rightarrow \;\;\:1\;\;\:,\;\;\:2\;\;\:,\;\;\:4\;\;\:,\;\;\: \cdots \)
دنباله هندسی
2 با توجه به مفهوم دنبالهٔ هندسی و نسبت مشترک جملات دنبالهٔ هندسی ثابت کنید هرگاه a و b و c سه جملهٔ متوالی یک دنبالهٔ هندسی باشند، آن گاه \(a \times c = {b^2}\) (b را واسطهٔ هندسی میان a و c می نامند.)
دنباله \(a\;,\;b\;,\;c\) ، یک دنباله هندسی است؛ بنابراین :
\(\begin{array}{l}a\;,\;b\;,\;c\;\; \Rightarrow \;\;r = \frac{b}{a} = \frac{c}{b}\\\\ \Rightarrow \;\;{b^2} = ac\end{array}\)
3 اگر x+3 و x+2 و x سه جملهٔ متوالی یک دنبالهٔ هندسی باشند، مقدار x را به دست آورید.
\(\begin{array}{l}x\:,\:x + 2\:,\:x + 3\;\;\: \Rightarrow \;{(x + 2)^2} = x\:(x + 3)\\\\ \Rightarrow {x^2} + 4x + 4 = {x^2} + 3x \Rightarrow x + 4 = 0\\\\ \Rightarrow x = - 4\end{array}\)
4 سرطان از تکثیر بیش از حد سلول ها در بدن ایجاد می شود. در فردی که به سرطان سینه 1 مبتلاست، از روش های مختلفی از جمله شیمی درمانی برای از بین بردن سلول های سرطانی استفاده می شود. در این روش معمولاً دارو چندین دفعه به بیمار تجویز می شود و هر بار درصدی از سلول های سرطانی از بین می رود.
الف اگر داروی شیمی درمانی هر بار 60% سلول های سرطانی فردی را از بین ببرد و اگر تودهٔ سرطانی او در ابتدا 1012 سلول داشته باشد، پس از 3 بار شیمی درمانی چه تعداد سلول سرطانی در بدن این فرد باقی می ماند؟
ب فرض کنید پس از اولین شیمی درمانی، رشد تودهٔ سرطانی متوقف شده است. برای اینکه این شخص به طور کامل درمان شود، ابتدا باید تعداد سلول های سرطانی اش به کمک شیمی درمانی کمتر از 106 × 7 سلول شود و سپس با کوچک شدن تودهٔ سرطانی به کمک جراحی، باقی ماندهٔ سلول های سرطانی او برداشته شود. برای این منظور، مطابق اطلاعات مسئله این شخص چند مرتبه باید شیمی درمانی شود؟
الف
\(\begin{array}{l}{a_n} = {10^{12}}{(\frac{4}{{10}})^{n - 1}}\quad \\\\ \Rightarrow {a_3} = {10^{12}}{(\frac{4}{{10}})^{3 - 1}} = {10^{12}}{(\frac{4}{{10}})^2}\\\\ = 1/6 \times {10^{11}}\end{array}\)
ب
\(\begin{array}{l}{10^{12}}{(\frac{4}{{10}})^{n - 1}} < 7 \times {10^6} \Rightarrow {(\frac{4}{{10}})^{n - 1}} < 7 \times {10^{ - 6}}\\\\n = 2 \Rightarrow 0/4 > 7 \times {10^{ - 6}}\\\\n = 3 \Rightarrow {(0/4)^2} = 0/16 > 7 \times {10^{ - 6}}\\\quad \vdots \\n = 13 \Rightarrow {(0/4)^{12}} = 1/6777 \times {10^{ - 5}} > 7 \times {10^{ - 6}}\\\\n = 14 \Rightarrow {(0/4)^{13}} = 6/7108 \times {10^{ - 6}} < 7 \times {10^{ - 6}}\\\\ \Rightarrow \quad n = 14\end{array}\)
5 میان دو عدد a و b ، n عدد را طوری قرار می دهیم که جملات دنبالهٔ شروع از a و ختم به b یک دنبالهٔ هندسی تشکیل دهند. ثابت کنید نسبت مشترک دنباله های هندسی از رابطهٔ \({r^{n + 1}} = \frac{b}{a}\) به دست می آید. (راهنمایی: تعداد کل جملات (n+2) جمله است.)
\(\begin{array}{l}a\;,\mathop {\underline {\quad \cdots \quad } }\limits_{n\;Sentence} ,\;b\quad \Rightarrow \quad n + 2\;Sentence\quad \\\\ \Rightarrow \quad \left\{ \begin{array}{l}{a_{n + 2}} = a\;{r^{n + 1}}\\{a_{n + 2}} = b\end{array} \right. \Rightarrow a\;{r^{n + 1}} = b\\\\ \Rightarrow {r^{n + 1}} = \frac{b}{a}\end{array}\)
sentecnce به معنی جمله است.
6 جملهٔ سوم یک دنبالهٔ هندسی 27 و جملهٔ پنجم همین دنباله 243 است. جملهٔ هفتم این دنبالهٔ هندسی را به دست آورید.
\(\begin{array}{l}{a_1}\;,\;{a_2}\;,\;\mathop {\underline{\underline {{a_3}}} }\limits_{27} \;,\;{a_4}\;,\;\mathop {\underline{\underline {{a_5}}} }\limits_{243} \;,\; \cdots \quad \\\\ \Rightarrow \quad \frac{{{a_5}}}{{{a_3}}} = \frac{{{a_1}\;{r^4}}}{{{a_1}\;{r^2}}} = {r^2} = \frac{{243}}{{27}} = 9\\\;\;\quad \;\\ \Rightarrow {a_7} = {a_1}\;{r^6} = {a_1}\;{r^4} \times {r^2} = 243 \times 9 = 2187\end{array}\)
7 مستطیلی با اضلاع a و b مطابق شکل مقابل مفروض است. اگر مربعی به ضلع x هم مساحت با آن باشد، کدام یک از دنباله های زیر تشکیل یک دنبالهٔ هندسی می دهند؟
الف) x و b و a
ب) b و x و a
پ) x و a و b
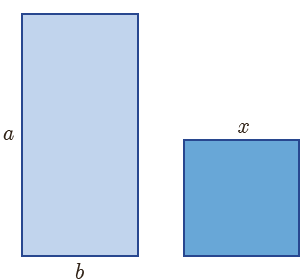
\({x^2} = a\;b\)
x واسطه هندسی بین a و b است؛ پس دنباله هندسی آن \(a\;,\;x\;,\;b\) یا \(b\;,\;x\;,\;a\) است. در نتیجه جواب گزینه ب می باشد.
8 یک شهاب سنگ ١٥ هزار کیلوگرم وزن دارد. پس از ورود آن به جوّ زمین، در هر دقیقه %15 از وزنش به سبب تماس با جو از بین می رود. پس از گذشت پنج دقیقه از ورود این شهاب سنگ به جوّ زمین، چقدر از وزن آن باقی می ماند؟
\(\begin{array}{l}{a_n} = 15000\;{(\frac{{85}}{{100}})^{n - 1}}\\\\ \Rightarrow {a_5} = 15000\;{(\frac{{85}}{{100}})^4} = 7830/09375\end{array}\)
9 شخصی پدر و مادر، دو پدر بزرگ و دو مادربزرگ، چهار پدر پدربزرگ و چهار مادر مادربزرگ و ... دارد.
الف نیاکان این شخص در ده نسل قبلی چند نفر بوده اند؟ (نخستین نسل را پدر و مادر شخص در نظر بگیرید.)
ب مجموع نیاکان این شخص از ده نسل قبل تا یک نسل قبل (یعنی پدر و مادر شخص) چند نفرند؟
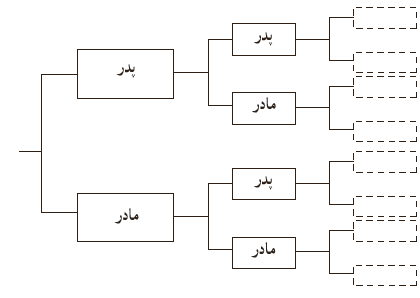
الف
\(\begin{array}{l}2\;,\;4\;,\;8\;,\; \cdots \quad \Rightarrow \quad {a_1} = 2\quad ,\quad r = 2\\\\{a_n} = 2 \times {2^{n - 1}} = {2^n}\quad \Rightarrow \quad {a_{10}} = {2^{10}} = 1024\end{array}\)
ب
\({S_n} = 2 \times \frac{{1 - {2^{10}}}}{{1 - 2}} = - 2 + {2^{11}} = - 2 + 2048 = 2046\)
10 مجموع های زیر را به دست آورید.
الف \(1 + 4 + 16 + … + 4096\)
ب \(\frac{1}{5} + \frac{1}{{10}} + \frac{1}{{20}} + \;...\; + \frac{1}{{640}}\)
الف \(1 + 4 + 16 + … + 4096\)
\(\begin{array}{*{20}{l}}\begin{array}{l}{a_1} = 1\;\;\:,\;\;\:r = 4\;\;\: \Rightarrow \;\;\:{a_n} = {4^{n - 1}} = 4096 = {4^6}\\\\ \Rightarrow n - 1 = 6 \Rightarrow n = 7\end{array}\\\begin{array}{l}\\{S_7} = \frac{{1\:(1 - {4^7})}}{{1 - 4}} = \frac{{ - 16383}}{{ - 3}} = 5461\end{array}\end{array}\)
ب \(\frac{1}{5} + \frac{1}{{10}} + \frac{1}{{20}} + \;...\; + \frac{1}{{640}}\)
\(\begin{array}{*{20}{l}}\begin{array}{l}{a_1} = \frac{1}{5}\;\;\:,\;\;\:r = \frac{1}{2}\;\; \Rightarrow \;\:{a_n} = \frac{1}{5}{(\frac{1}{2})^{n - 1}} = \frac{1}{{640}}\\\\ \Rightarrow {(\frac{1}{2})^{n - 1}} = \frac{1}{{128}} = {(\frac{1}{2})^7} \Rightarrow n - 1 = 7 \Rightarrow n = 8\end{array}\\\begin{array}{l}\\{S_8} = \frac{{\frac{1}{5}\:(1 - {{(\frac{1}{2})}^8})}}{{1 - \frac{1}{2}}} = \frac{{2 - {{(\frac{1}{2})}^7}}}{5} = \frac{{2 - \frac{1}{{128}}}}{5} = \frac{{255}}{{640}} = \frac{{51}}{{128}}\end{array}\end{array}\)
11 نخستین جملهٔ یک دنبالهٔ هندسی 1536 و نسبت مشترک این دنبالهٔ هندسی \(\frac{1}{2}\) است. کدام جملهٔ دنباله برابر 6 است؟ مجموع جملات این دنباله از 1536 تا عدد 6 را به دست آورید.
\(\begin{array}{*{20}{l}}{{a_1} = 1536\;\;\:,\;\;\:r = \frac{1}{2}\;\;\:,\;\;\:{a_n} = 6\;\;\:,\;\;\: \Rightarrow n = ?}\\\begin{array}{l}\\{a_n} = 1536\:{(\frac{1}{2})^{n - 1}} = 6 \Rightarrow {(\frac{1}{2})^{n - 1}} = \frac{1}{{256}} = {(\frac{1}{2})^8}\\\\ \Rightarrow n - 1 = 8 \Rightarrow n = 9\end{array}\\\begin{array}{l}\\{S_9} = \frac{{1536\:(1 - {{(\frac{1}{2})}^9})}}{{1 - \frac{1}{2}}} = \frac{{1536\: - \frac{{1536}}{{512}}}}{{\frac{1}{2}}}\\\\ = 2 \times 1536 - \frac{{1536}}{{256}} = 3072 - 6 = 3066\end{array}\end{array}\)
12 پس از تقسیم مربعی به ضلع یک متر به چهار مربع برابر، یکی از آنها را رنگ می کنیم. از مربع های باقی مانده، مربعی را که با مربع رنگ آمیزی شده ضلع مشترک ندارد،انتخاب می کنیم و با تقسیم آن به چهار مربع برابر، مربعی را که با مربع رنگ شده در یک رأس مشترک است، رنگ آمیزی می کنیم و همین روند را مطابق شکل ادامه می دهیم.
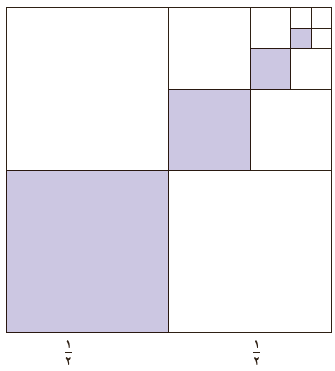
الف چرا دنبالهٔ مساحت های مربع های رنگی، یک دنبالهٔ هندسی را تشکیل می دهد؟
ب اگر روند رنگ آمیزی گفته شده را n مرحله انجام دهیم، مجموع مساحت های مربع های رنگی از چه رابطه ای به دست می آید؟
پ پس از شش مرحله رنگ آمیزی مربع به روش بالا، چه مساحتی از مربع رنگ می شود؟
الف زیرا مساحت هر قسمت از ضرب مساحت قسمت قبلی در \(\frac{1}{2}\) به دست می آید.
ب
\({S_n} = \frac{1}{4} \times \frac{{1 - {{(\frac{1}{4})}^n}}}{{1 - \frac{1}{4}}} = \frac{{1 - {{(\frac{1}{4})}^n}}}{3}\)
پ
\({S_6} = \frac{{1 - {{(\frac{1}{4})}^6}}}{3} = \frac{{1 - \frac{1}{{4096}}}}{3} = \frac{{4095}}{{12288}}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















