1736019749.png)
جواب فعالیت صفحه 86 درس 3 ریاضی و آمار دوازدهم انسانی (الگوهای غیر خطی)
تعداد بازدید : 78.8Mپاسخ فعالیت صفحه 86 ریاضی و آمار دوازدهم انسانی
-گام به گام فعالیت صفحه 86 درس الگوهای غیر خطی
-فعالیت صفحه 86 درس 3
-شما در حال مشاهده جواب فعالیت صفحه 86 ریاضی و آمار دوازدهم انسانی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
1 حاصل عبارت های زیر را به دست آورید.
\(\begin{array}{l}{4^3} = \\\\{\left( 2 \right)^{ - 7}} = \\\\{\left( {\frac{2}{5}} \right)^4} = \\\\{73^1} = \\\\{\left( { - 3} \right)^6} = \\\\ - {3^6} = \\\\{\left( {0/01} \right)^5} = \\\\{\left( {1\frac{1}{2}} \right)^0} = \end{array}\)
\({4^3} = 64\)
\({\left( 2 \right)^{ - 7}} = {\left( {\frac{1}{2}} \right)^7} = \frac{1}{{128}}\)
\({\left( {\frac{2}{5}} \right)^4} = \frac{{{2^4}}}{{{5^4}}} = \frac{{16}}{{625}}\)
\({73^1} = 73\)
\({\left( { - 3} \right)^6} = 729\)
\( - {3^6} = - 729\)
\({\left( {0/01} \right)^5} = 1 \times {10^{ - 10}}\)
\({\left( {1\frac{1}{2}} \right)^0} = 1\)
2 الف مانند نمونه، حاصل هر یک از عبارت های زیر را به صورت عدد توان دار بنویسید و در جدول در جای مناسب قرار دهید. (m و n اعداد صحیح و a و b اعداد حقیقی مخالف صفرند.)
\(\begin{array}{l}{\left( { - 36} \right)^7} \div {9^7} = \\\\{\left( {2/1} \right)^6} \times \left( {\frac{{21}}{{10}}} \right) \times {\left( {2\frac{1}{{10}}} \right)^4} = {\left( {2/1} \right)^{11}}\\\\{\left( { - 4} \right)^3} \times {\left( { - 5} \right)^3} = \\\\{\left( {\frac{4}{7}} \right)^5} \div {\left( {\frac{4}{7}} \right)^8} = \\\\{\left( {{{10}^6}} \right)^8} = \end{array}\)
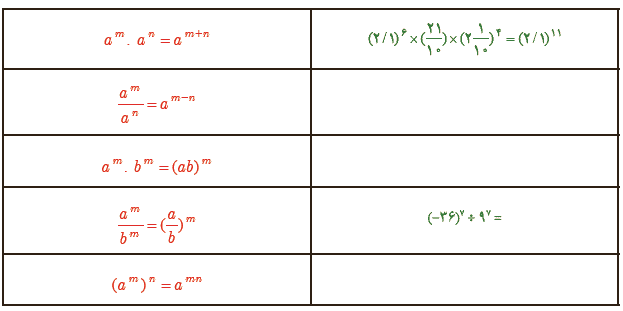
ب مانند نمونه، برای هر یک از رابطه ها یا مثال های زیر، رابطه یا مثال متناظر بنویسید.
الف
\(\begin{array}{l}{\left( { - 36} \right)^7} \div {9^7} = {\left( {\frac{{ - 36}}{9}} \right)^7} = {\left( { - 4} \right)^7}\\\\{\left( {2/1} \right)^6} \times \left( {\frac{{21}}{{10}}} \right) \times {\left( {2\frac{1}{{10}}} \right)^4} = {\left( {2/1} \right)^{11}}\\\\{\left( { - 4} \right)^3} \times {\left( { - 5} \right)^3} = {\left( {\left( { - 4} \right) \times \left( { - 5} \right)} \right)^3} = {20^3}\\\\{\left( {\frac{4}{7}} \right)^5} \div {\left( {\frac{4}{7}} \right)^8} = {\left( {\frac{4}{7}} \right)^{5 - 8}} = {\left( {\frac{4}{7}} \right)^{ - 3}} = {\left( {\frac{7}{4}} \right)^3} = \frac{{343}}{{64}}\\\\{\left( {{{10}^6}} \right)^8} = {10^{6 \times 8}} = {10^{48}}\end{array}\)
ب
3 همان طور که می دانید، اگر a، یک عدد حقیقی مثبت باشد \(\sqrt a \) و \( - \sqrt a \) ریشه های دوم عدد a هستند. به عبارت دیگر، ریشه های دوم عدد a همان ریشه های معادلهٔ درجهٔ دوم x2=a هستند. برای مثال، ریشه های دوم عدد 16 ریشه های معادلهٔ x2=16 می باشند و چون 16=42 و \({\left( { - 4} \right)^2} = 16\)، پس 4 و 4- یا \(\sqrt {16} \) و \( - \sqrt {16} \) ریشه های دوم عدد 16 هستند. همچنین، ریشهٔ سوم عدد حقیقی مانند a، ریشۀ معادلۀ x3=a است. برای مثال، ریشهٔ سوم عدد 27، ریشهٔ معادلهٔ x2=27 است که برابر 3 می باشد.
با همین استدلال، ریشهٔ پنجم عدد 32-، پاسخ معادلهٔ x5=-32 است که برابر _____ و ریشه های ششم عدد 64 ، ریشه های معادلهٔ x6=___ هستند که برابر 2+ و 2- می باشند.
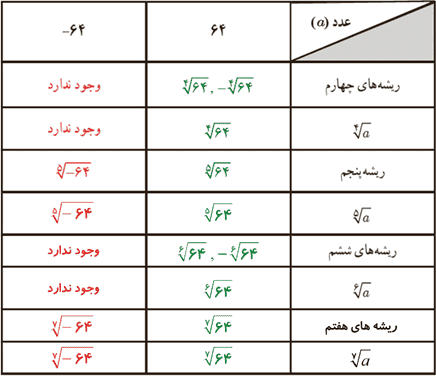
جدول صفحهٔ بعد را مانند نمونه کامل کنید.
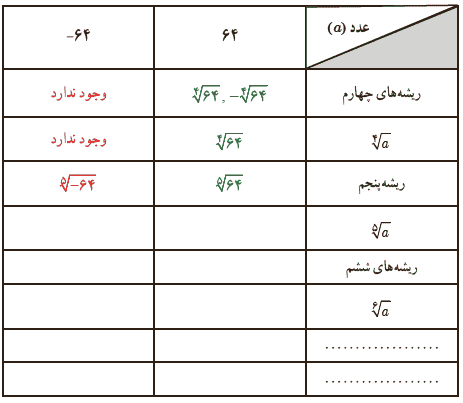
با همین استدلال، ریشهٔ پنجم عدد 32-، پاسخ معادلهٔ x5=-32 است که برابر 2- و ریشه های ششم عدد 64، ریشه های معادلهٔ x6=64 هستند که برابر 2+ و 2- می باشند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
