جواب تمرین صفحه 71 درس 2 ریاضی و آمار دوازدهم انسانی (الگوهای خطی)
تعداد بازدید : 84.71Mپاسخ تمرین صفحه 71 ریاضی و آمار دوازدهم انسانی
-گام به گام تمرین صفحه 71 درس الگوهای خطی
-تمرین صفحه 71 درس 2
-شما در حال مشاهده جواب تمرین صفحه 71 ریاضی و آمار دوازدهم انسانی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 با نوشتن جملات رابطه های بازگشتی، مشخص کنید کدام یک دنبالهٔ حسابی است.
الف \({a_{n + 1}} = \frac{1}{{{a_n}}}\;\;\;\;{a_1} = 2\)
ب \({a_{n + 1}} = {a_n} + 5\;\;\;\;{a_1} = - 1\)
ج \({a_{n + 1}} = 5{a_n} + 1\;\;\;\;{a_1} = - 1\)
د \({a_{n + 1}} - {a_n} = n\)
الف \(2\;\;,\;\;\frac{1}{2}\;\;,\;\;2\;\;,\;\;\frac{1}{2}\;\;,\;\; \cdots \)
ب \( - 1\;\;,\;\;4\;\;,\;\;9\;\;,\;\;14\;\;,\;\; \cdots \)
ج \( - 1\;\;,\;\; - 4\;\;,\;\; - 19\;\;,\;\; - 94\;\;,\;\; \cdots \)
د
\(\begin{array}{l}{a_1} = k\;\; \Rightarrow \;\;\\\\k\:,\:k + 1\:,\:k + 3\:,\:k + 6\:,\:k + 10\:,\:k + 15\:,\: \cdots \end{array}\)
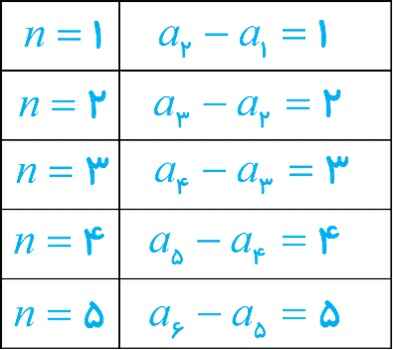
اگر k=1 :
\({a_n}:\:1\;,\;2\;,\;4\;,\;7\;,\;11\;,\;15\;,\;\: \cdots \)
دنباله بند ب یک دنباله حسابی است، ولی بقیه دنباله نیستند.
2 در یک دنبالهٔ حسابی، جملهٔ اول برابر 5- و اختلاف مشترک برابر 8 است. کدام جملهٔ دنباله برابر 555 است؟
\(\begin{array}{l}{a_n} = {a_1} + (n - 1)d \Rightarrow 555 = - 5 + 8(n - 1)\\\\ \Rightarrow 560 = 8n - 8\\\\ \Rightarrow 568 = 8n \Rightarrow n = 71\end{array}\)
3 یازدهمین جملهٔ یک دنبالهٔ حسابی 52 و جملهٔ نوزدهم آن 92 است. جملهٔ سی اُم این دنباله را مشخص کنید.
\(\begin{array}{l}{a_n} = {a_1} + (n - 1)d\\\\\mathop \Rightarrow \limits^{{a_1} = a} \;\left\{ {\begin{array}{*{20}{l}}{{a_{11}} = a + 10d \Rightarrow a + 10d = 52}\\{{a_{19}} = a + 18d \Rightarrow a + 18d = 92}\end{array}} \right.\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{a_1} = a = 2}\\{d = 5}\end{array}} \right.\\\\{a_{30}} = {a_1} + 29d = 2 + 29 \times 5 = 147\end{array}\)
4 برای کاهش مصرف آب در کشاورزی یک منطقه، از آبیاری قطره ای استفاده می شود؛ به این صورت که یک میله که در آن سوراخ هایی برای پخش آب تعبیه شده است، به کمک چرخ هایی (مطابق شکل مقابل) حول یک محور می چرخد. اگر فاصلهٔ اولین چرخ تا موتور 3 متر و بعد از آن، فاصلهٔ هر چرخ تا چرخ بعدی 5 متر باشد و در کل، 12 چرخ روی میله قرار داشته باشد، با این وسیله چه مساحتیپ آبیاری می شود؟ (آخرین چرخ دقیقاً در انتهای میله قرار دارد.)

\(\begin{array}{l}{a_n} = {a_1} + (n - 1)d\\\\ \Rightarrow {a_{12}} = 3 + (12 - 1)(5) = 58\end{array}\)
فاصله دوازدهمین (آخرین) چرخ تا موتور برابر 58 متر است که برابر شعاع دایره ای است که این میله آبیاری می کند.
مساحت آبیاری شده:
\(S = \pi {(58)^2} \simeq 10562/96\) متر مربع
5 در یک کارخانهٔ سنگ بری برای صیقل دادن سنگ ها از یک صفحه به وزن 12500 گرم استفاده می شود. اگر با توجه به مصرف هفتگی به طور میانگین 1875 گرم از وزن صفحه کم شود، پس از شش هفته استفادهٔ مداوم وزن صفحه چقدر است؟
\(\begin{array}{l}{a_1} = 12500 - 1875 = 10625\\{a_2} = 10625 - 1875 = 8750\\{a_3} = 8750 - 1875 = 6875\\{a_4} = 6875 - 1875 = 5000\end{array}\)
این دنباله یک دنباله حسابی است و در آن a1=10625 و d=1875 ؛ پس :
\(\begin{array}{l}{a_n} = {a_1} + (n - 1)d\\\\ \Rightarrow {a_6} = 10625 + (6 - 1)( - 1875) = 1250\end{array}\)
وزن صفحه پس از 6 هفته (گرم)
6 میان دو عدد a و b ، n عدد را به گونه ای قرار می دهیم که جملات دنباله از a تا b یک دنبالهٔ حسابی تشکیل دهند. ثابت کنید اختلاف مشترک جملات دنباله از رابطهٔ \(d = \frac{{b - a}}{{n + 1}}\) به دست می آید. (توجه داشته باشید که تعداد کل جملات (n+1) جمله است.)
می توان دنباله ای حسابی در نظر گرفت که جمله اول آن a و جمله آخر آن b باشد. اگر قرار است بین b و a به تعداد m جمله قرار گیرد. در این صورت واضح است که این دنباله دارای n=m+2 جمله است:
\(\begin{array}{l}\left\{ \begin{array}{l}{a_1} = a\\{a_n} = b\end{array} \right.\;\; \Rightarrow \;\;{a_n} - {a_1} = b - a\\\\ \Rightarrow ({a_1} + (n - 1)d) - {a_1} = b - a\\\\ \Rightarrow (n - 1)d = b - a\\\\ \Rightarrow d = \frac{{b - a}}{{n - 1}}\\\\\mathop \Rightarrow \limits^{n = m + 2} \;d = \frac{{b - a}}{{(m + 2) - 1}} = d = \frac{{b - a}}{{m + 1}}\end{array}\)
7 براساس رابطهٔ به دست آمده در مسئلهٔ 6، سه عدد را به گونه ای میان اعداد 10 و 18 قرار دهید که یک دنبالهٔ حسابی تشکیل دهند.
\(d = \frac{{b - a}}{{m + 1}}\;\; \Rightarrow \;\;d = \frac{{18 - 10}}{{3 + 1}} = 2\)
لذا دو دنباله زیر را می توان نوشت:
10 , 12 , 14 , 16 , 18
18 , 16 , 14 , 12 , 10
8 مجموع عددهای زیر را به دست آورید.
الف 1 , 5 , 9 , ….. , 401
ب 89 , 85 , 81 , …… , 13
الف اگر b جمله آخر و a جمله اول یک دنباله حسابی باشد، در این صورت :
\(b = a + (n - 1)d\)
لذا می توان نتیجه گرفت :
\(n = \frac{{b - a}}{d} + 1\)
در اینجا نیز می توان نوشت :
\(\begin{array}{l}n = \frac{{b - a}}{d} + 1 = \frac{{401 - 1}}{4} + 1 = 101\\\\ \Rightarrow S = \frac{n}{2}(a + b) = \frac{{101}}{2}(401 + 1)\\\\ = 101 \times 201 = 20301\end{array}\)
ب
\(\begin{array}{l}n = \frac{{b - a}}{d} + 1 = \frac{{13 - 89}}{{ - 4}} + 1 = 20\\\\ \Rightarrow S = \frac{n}{2}(a + b) = \frac{{20}}{2}(89 + 13)\\\\ = 10 \times 102 = 1020\end{array}\)
9 باغ داران برای چیدن میوه ها از نردبان هایی استفاده می کنند که بخشی از آنها که روی زمین قرار می گیرد، برای تعادل بیشتر، عرض بیشتری دارد و انتهای نردبان که به درخت تکیه داده می شود، برای جابه جایی آسان تر و تکیه گاه بهتر، عرض کمتری دارد.
اگر عرض نخستین پلهٔ این نردبان 125 سانتی متر و عرض آخرین پلهٔ آن 45 سانتی متر در نظر گرفته شود و هر پله 10 سانتی متر کوتاه تر از پلهٔ پیشین باشد، این نردبان چند پله خواهد داشت؟ برای ساخت پله ها به چند متر چوب احتیاج خواهیم داشت؟

می توان یک دنباله حسابی در نظر گرفت که در آن جمله اول 125 و جمله آخر 45 و اختلاف مشترک 10- باشد. در این مسئله تعداد جملات و مجموع جملات مورد نظر برابر است با :
\(\begin{array}{l}n = \frac{{b - a}}{d} + 1 = \frac{{125 - 45}}{{ - 10}} + 1 = 9\\\\S = \frac{n}{2}(a + b) = \frac{9}{2}(125 + 45) = 9 \times 85 = 765\end{array}\)
765 سانتی متر یا 7/65 متر
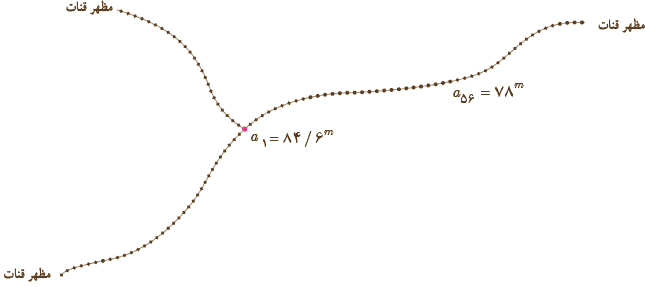
10 ارزش امروزی قنات زارچ، طولانی ترین قنات ایران _ عمق مادرچاه قنات زارچ 84/6 متر است که از آن سه شاخه قنات خارج شده است. اگر تعداد میله های هر سه شاخه قنات برابر و عمق پنجاه و ششمین چاه (میلۀ 55ام) 78 متر باشد، با فرض اینکه شیب زمین ثابت و فاصلهٔ میان هر دو میله یکسان باشد و عمق آخرین چاه قنات (میله) 120 سانتی متر درنظر گرفته شود:
الف هر شاخه قنات دارای چند میله است؟
ب مجموع طول چاه های حفرشده در این مسیر چقدر است؟ مجموع طول چاه های حفرشده در کل قنات چقدر است؟
ج اگر میانگین هزینهٔ حفر یک متر چاه (شامل حفر، مصالح و دیوارچینی) 250 هزار تومان باشد، هزینهٔ حفر چاه های قنات در حال حاضر چقدر است؟
د طبق محاسبات مهندسی، در قنات زارچ در مجموع طول کل کانال قنات 71 کیلومتر است. با توجه به میانگین هزینهٔ 350 هزار تومان برای حفر کانال قنات، ارزش کل قنات زارچ چقدر است؟ (راهنمایی: an را عمق چاه nاُم تا کانال قنات و a1 را عمق مادر چاه در نظر بگیرید.)
پاسخ:
الف 696 چاه شامل یک مادرچاه و 695 میله
ب مجموع طول چاه ها در یک مسیر 29858/4 متر و مجموع طول چاه ها در کل قنات 89406 متر
ج 22,351,500,00 تومان
د 47,201,500,000 تومان
الف
\(\begin{array}{l}{a_{56}} = {a_1} + (n - 1)d\\\\ \Rightarrow 78 = 84/6 + 55d\\\\ \Rightarrow d = \frac{{78 - 84/6}}{{55}} = - 0/12\\\\{a_n} = {a_1} + (n - 1)d\\\\ \Rightarrow 1/2 = 84/6 + (n - 1)( - 0/12)\\\\ \Rightarrow n - 1 = \frac{{1/2 - 84/6}}{{ - 0/12}} = 695\\\\ \Rightarrow n = 696\end{array}\)
ب
متر \({S_n} = \frac{{696}}{2}(84/6 + 1/2) = 29858/4\)
مجموع طول چاه های حفر شده در یک مسیر است. برای اینکه مجموع طول چاه های حفر شده در کل قنات را بدست آوریم، بایستی مجموع طول چاه های حفر شده در یک مسیر را 3 برابر کنیم، ولی باید در نظر بگیریم که طول چاه مادر هم 3 بار حساب می شود که در نهایت باید 2 برابر طول چاه مادر را از عدد بدست آمده کم کنیم؛ یعنی :
مجموع طول چاه های حفر شده در کل قنات:
متر \(29858/4 \times 3 - 84/6 \times 2 = 89406\)
ج هزینه حفر چاه های قنات:
89406 \times 250,000 = 22,351,500,000 تومان
د هزینه حفر کانال:
\(71,000 \times 350,000 = 24,850,000,000\) تومان
ارزش حفاری قنات زارچ برابر است با مجموع هزینه حفر چاه های قنات و هزینه حفر کانال قنات؛ در نتیجه :
ارزش حفاری قنات زارچ:
\(22,351,500,000 + 24,850,000,000 = 47,201,500,000\) تومان
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















