جواب تمرین صفحه 57 درس 2 ریاضی و آمار دوازدهم انسانی (الگوهای خطی)
تعداد بازدید : 84.72Mپاسخ تمرین صفحه 57 ریاضی و آمار دوازدهم انسانی
-گام به گام تمرین صفحه 57 درس الگوهای خطی
-تمرین صفحه 57 درس 2
-شما در حال مشاهده جواب تمرین صفحه 57 ریاضی و آمار دوازدهم انسانی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 برای محاسبهٔ قبض آب 1 (آب بها) هر واحد مسکونی در شهر تهران ابتدا میانگین مصرف هر واحد مسکونی محاسبه می شود و بر اساس آن «طبقۀ مصرفی» واحد مسکونی با توجه به «جدول 1» تعیین می گردد. آنگاه به کمک رابطهٔ زیر، آب بها محاسبه می شود:
آب بها = میانگین مصرف × هزینهٔ هر متر مکعب با توجه به طبقهٔ مصرف
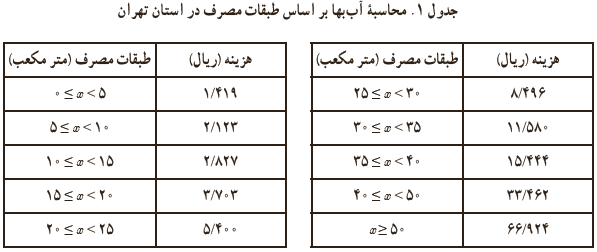
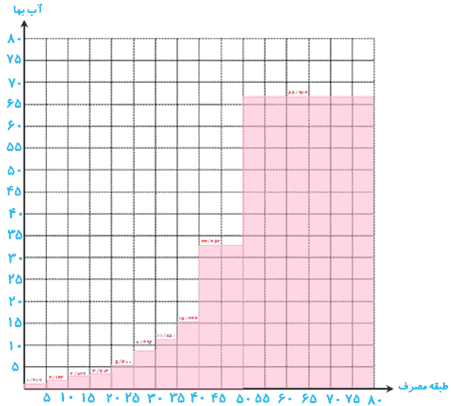
الف نمودار «طبقه مصرف _ آب بها» جدول بالا را رسم کنید و ضابطه و دامنه و برد تابع را به دست آورید.
ب اگر میانگین مصرف یک واحد مسکونی در تهران در یک ماه 20/49 m2 باشد، سطح زیر منحنی نمودار چه تابعی، آب بها را مشخص می کند؟
الف
\(\begin{array}{l}f(x) = \left\{ {\begin{array}{*{20}{l}}{1/419\:x\;\;\:,\;\;\:0 \le x < 5}\\{2/123\:x\;\;\:,\;\;\:5 \le x < 10}\\{2/827\:x\;\;\:,\;\;\:10 \le x < 15}\\{3/703\:x\;\;\:,\;\;\:15 \le x < 20}\\{5/400x\;\;\:,\;\;\:20 \le x < 25}\\{8/496\:x\;\;\:,\;\;\:25 \le x < 30}\\{11/850\:x\;\;\:,\;\;\:30 \le x < 35}\\{15/444\:x\;\;\:,\;\;\:35 \le x < 40}\\{33/462\:x\;\;\:,\;\;\:40 \le x < 50}\\{66/924\:x\;\;\:,\;\;\:50 \le x}\end{array}} \right.\\\\\begin{array}{*{20}{l}}\begin{array}{l}{D_f} = \left\{ {x \in \mathbb{R}|x \ge 0} \right\}\\\end{array}\\{{R_f} = \left\{ {y \in \mathbb{R}|y \ge 0} \right\}}\end{array}\end{array}\)
ب
\(\begin{array}{l}f(x) = 5/400\:x\;\;\:,\;\;\:20 \le x < 25\;\;\:\\\\ \Rightarrow \;\;\:f(20/49) = 5/400\: \times 20/49 = 110/646\end{array}\)
110/646 ریال
2 اگر تابع f مدل ریاضی هرکدام از مسائل زیر باشد، دامنهٔ هرکدام از آنها را مشخص کنید.
الف کاهش دمای هوا با دور شدن از سطح زمین تا ارتفاع 15 کیلومتر R N
ب میزان استفادهٔ دانش آموزان یک مدرسه از اینترنت در هر ساعت R N
ج حجم مکعبی به ضلع R N
د تغییرات سطح دریاچهٔ ارومیه در بیست سال اخیر R N
هـ میزان مصرف ماهیانهٔ آب در یک واحد مسکونی R N
الف کاهش دمای هوا با دور شدن از سطح زمین تا ارتفاع 15 کیلومتر R
ب میزان استفادهٔ دانش آموزان یک مدرسه از اینترنت در هر ساعت N
ج حجم مکعبی به ضلع R
د تغییرات سطح دریاچهٔ ارومیه در بیست سال اخیر R
هـ میزان مصرف ماهیانهٔ آب در یک واحد مسکونی R
3 نمودار زیر درصد جمعیتی از سراسر جهان را نشان می دهد که از 1993 که سال گسترش اینترنت در دنیاست، از اینترنت: استفاده کرده اند.
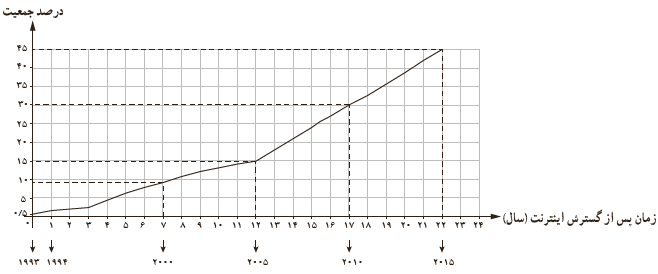
الف اگر f(n) درصد استفاده کنندگان از اینترنت در جهان، n سال پس از گسترش اینترنت باشد، به کمک نمودار داده شده مقادیر f(1) و f(3) را مشخص کنید و معنای آن را توضیح دهید.
ب با توجه به مدل خطی استفاده کنندگان از اینترنت از سال 2005 تا 2015 ، با به دست آوردن ضابطهٔ تابع خطی، در سال 2020 درصد استفاده کنندگان از اینترنت در جهان چقدر خواهد بود؟
الف f(1)=0/5 درصد استفاده از اینترنت در سال اول و f(7)=9 درصد استفاده از اینترنت در سال هفتم را نشان می دهد.
ب

شیب خط:
\(m = \frac{{45 - 15}}{{2015 - 2005}} = \frac{{30}}{{10}} = 3\)
عرض از مبدأ:
\(h = {y_0} - m{t_0} = 15 - 3(2005) = 15 - 6015 = - 6000\)
معادله خط:
\(y = mt + h \to y = 3t - 6000\)
ضابطه خطی تابع:
\(f(t) = 3t - 6000\)
درصد استفاده از اینترنت در سال 2020
\(f(2020) = 3(2020) - 6000 = 6060 - 6000 = 60\)
4 اگر جملات یک دنباله از قانون تابع خطی y=4x-1 پیروی کنند، با توجه به دامنهٔ دنباله:
الف نمودار تابع را رسم کنید و نمودار دنباله را روی نمودار تابع مشخص کنید.
ب نمایش تابعی دنباله و نیز رابطهٔ بازگشتی دنباله را بنویسید. شیب خط چه ارتباطی با رابطهٔ بازگشتی دنباله دارد؟
الف
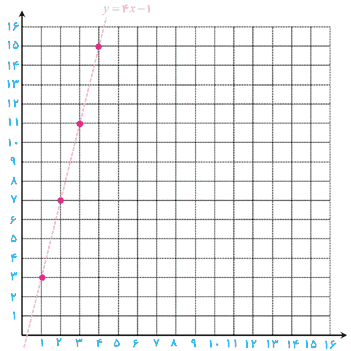
ب
\(\begin{array}{l}{a_n} = 4n - 1\quad ,\quad n \in \mathbb{N}\\\\\left\{ \begin{array}{l}{a_{n + 1}} = {a_n} + 4\\{a_1} = 3\end{array} \right.\end{array}\)
شیب خط برابر 4 می باشد. به طور کلی: (m شیب خط)
5 با توجه به دنباله های \({d_n} = {n^2} - 1\;,\;{c_n} = \frac{1}{{3n - 1}}\;,\;{b_n} = {\left( { - \frac{1}{2}} \right)^{n + 1}}\;,\;{a_n} = {3^n}\) حاصل عبارت های خواسته شده را به دست آورید.
الف a2 + b1
ب c2 – d1
ج b4 + d2
الف
\(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}{a_2} = {3^2} = 9\\\end{array}\\\\{{b_1} = {{( - \frac{1}{2})}^{1 + 1}} = \frac{1}{4}}\end{array}} \right.\)
ب
\(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}{a_2} = {3^2} = 9\\\end{array}\\\\{{b_1} = {{( - \frac{1}{2})}^{1 + 1}} = \frac{1}{4}}\end{array}} \right.\)
ج
\(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}{b_4} = {( - \frac{1}{2})^{4 + 1}} = - \frac{1}{{32}}\\\end{array}\\\\{{d_2} = {2^2} - 1 = 3}\end{array}} \right.\)
6 جملهٔ پنجم دنباله های بازگشتی زیر را مشخص کنید.
الف \({a_{n + 1}} = \frac{1}{3}{a_n}\;\;,\;\;{a_1} = - 2\)
ب \({a_{n + 1}} = \frac{1}{{1 + {a_n}}}\;\;,\;\;{a_1} = 1\)
ج \({a_{n + 3}} = {a_n} + {a_{n + 1}} + {a_{n + 2}}\;\;,\;\;{a_1} = {a_2} = {a_3} = 1\)
د \({a_{n + 1}} = {a_n} + {\left( { - 1} \right)^n}\;\;,\;\;{a_1} = 1\)
الف
\(\begin{array}{l}{a_1} = - \:2\;,\;{a_2} = - \:\frac{2}{3}\;,\;{a_3} = - \:\frac{2}{9}\;,\\\\{a_4} = - \:\frac{2}{{27}}\;,\;{a_5} = - \:\frac{2}{{81}}\end{array}\)
ب
\({a_1} = 1\;,\;{a_2} = \frac{1}{2}\;,\;{a_3} = \frac{2}{3}\;,\;{a_4} = \frac{3}{5}\;,\;{a_5} = \frac{5}{8}\)
ج
\({a_1} = 1\;,\;{a_2} = 1\;,\;\:{a_3} = 1\;,\;{a_4} = 3\;,\;{a_5} = 5\)
د
\({a_1} = 1\;,\;{a_2} = 0\:,\;{a_3} = 1\;,\;{a_4} = 0\;,\;{a_5} = 0\)
7 جدول زیر را کامل کنید.
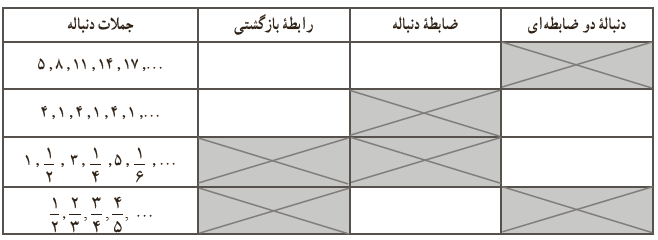
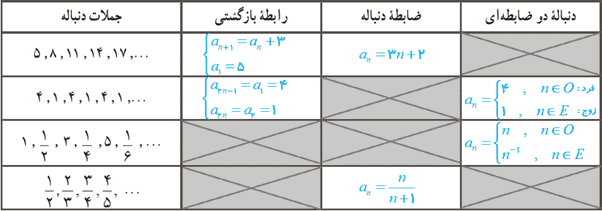
8 شش جملهٔ اوّل دنبالهٔ بازگشتی را برای هرکدام از حالت های زیر بنویسید.
الف a1=11
ب a1=25
الف \({a_1} = 11\;,\;34\;,\;17\;,\;52\;,\;26\;,\;79\)
ب \({a_1} = 25\;,\;76\;,\;38\;,\;115\;,\;\frac{{115}}{2}\;,\;\frac{{123}}{2}\)
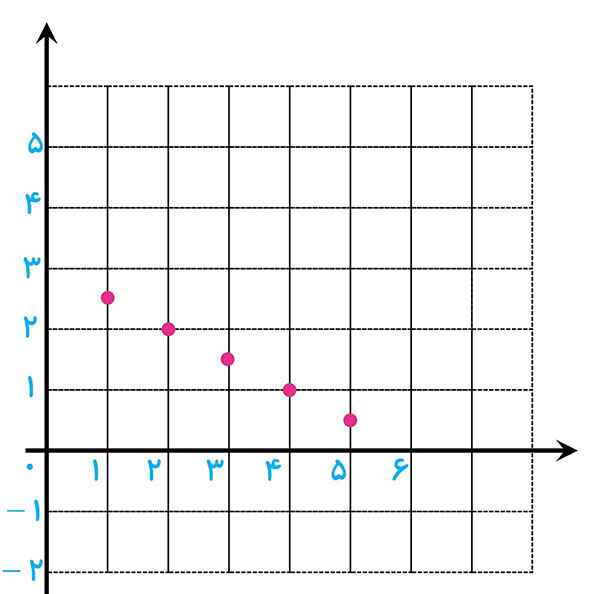
9 نمودار دنباله های زیر را برای \(n \le 5\) رسم کنید.
الف \({a_n} = - \frac{1}{2}n + 3\)
ب \({a_n} = {\left( { - \frac{1}{2}} \right)^n}\)
ج \({a_{n + 1}} = \frac{1}{{{a_n}}}\;\;\;\;{a_1} = 2\)
د
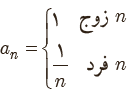
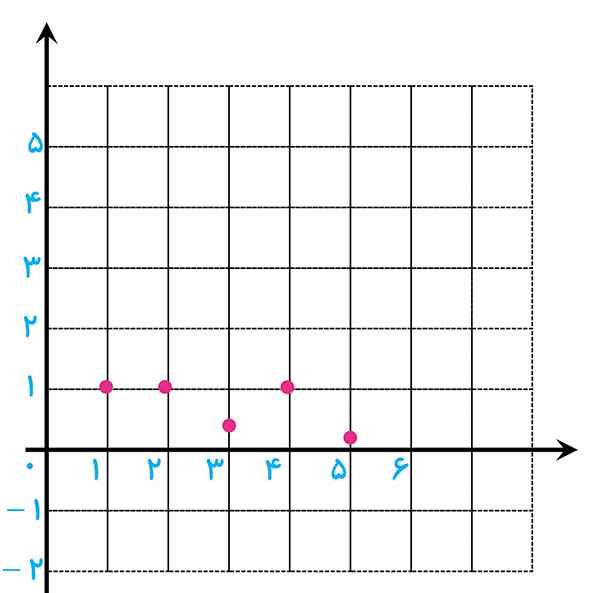
الف \({a_n}:\;\frac{5}{2}\;\;,\;\;2\;\;,\;\;\frac{3}{2}\;\;,\;\;1\;\;,\;\;\frac{1}{2}\)
ب \({a_n}:\; - \:\frac{1}{2}\;\;,\;\;\frac{1}{4}\;\;,\;\; - \:\frac{1}{8}\;\;,\;\;\frac{1}{{16}}\;\;,\;\; - \:\frac{1}{{32}}\)
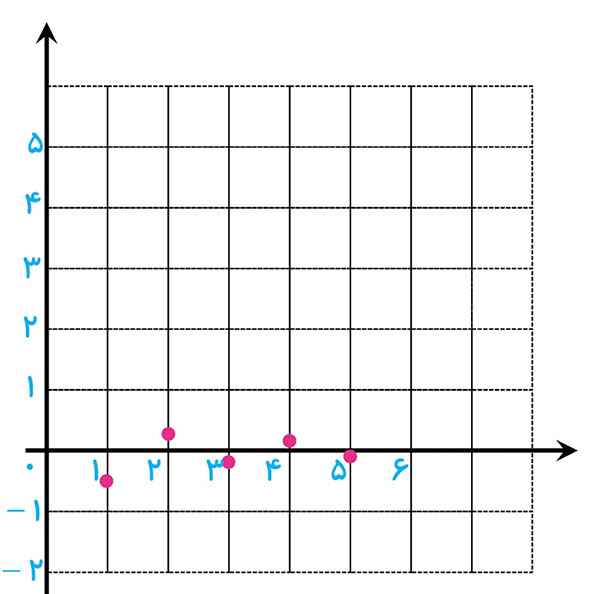
ج \({a_n}:\;\;2\;\;,\;\;\frac{1}{2}\;\;,\;\;2\;\;,\;\;\frac{1}{2}\;\;,\;\;2\)
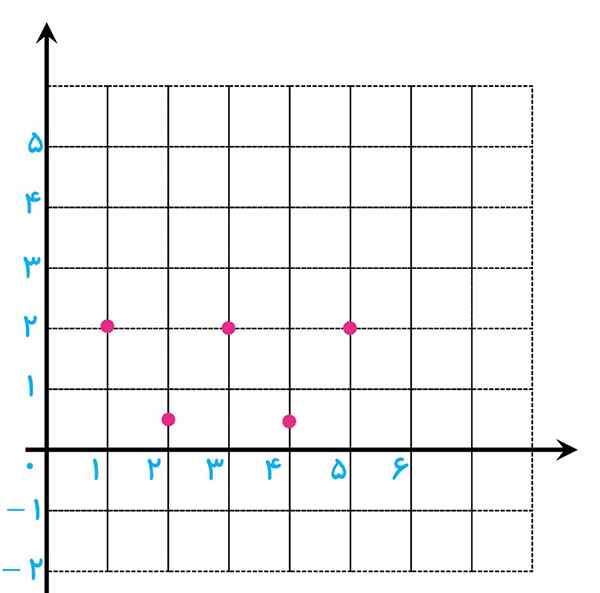
د \({a_n}:\;\;1\;\;,\;\;1\;\;,\;\;\frac{1}{3}\;\;,\;\;1\;\;,\;\;\frac{1}{5}\)
10 محاسبۀ جذر اعداد در تمدن بابل با نوشتن جملات دنبالهٔ بازگشتی زیر می توانیم به طرز شگفت انگیزی به جذر عدد k یعنی \(\sqrt k \) نزدیک شویم.
\({a_{n + 1}} = \frac{1}{2}\,\left( {{a_n} + \frac{k}{{{a_n}}}} \right)\;\;\;\;{a_1} = k\)
این روش منسوب به تمدن بابل (واقع در شرق ایران و در بین النهرین) است.
به کمک دنبالهٔ بازگشتی بالا، اگر a3 را تقریبی برای در نظر بگیریم، حاصل اعداد زیر را مشخص کنید.
الف \(\sqrt 2 \)
ب \(\sqrt 3 \)
ج \(\sqrt 5 \)
آیا این روش مزیتی بر استفاده از ماشین حساب دارد؟ چرا؟
الف
\(\begin{array}{l} \Rightarrow {a_{n + 1}} = \frac{1}{2}({a_n} + \frac{2}{{{a_n}}})\;\;\:;\;\;\:{a_1} = 2\\\\{a_2} = \frac{1}{2}({a_1} + \frac{2}{{{a_1}}}) = \frac{1}{2}(2 + \frac{2}{2}) = \frac{3}{2}\\\\{a_3} = \frac{1}{2}({a_2} + \frac{2}{{{a_2}}}) = \frac{1}{2}(\frac{3}{2} + \frac{2}{{\frac{3}{2}}})\\\\ = \frac{1}{2}(\frac{3}{2} + \frac{4}{3}) = \frac{1}{2} \times \frac{{17}}{6} = \frac{7}{{12}} \simeq 1/416\end{array}\)
ب
\(\begin{array}{l} \Rightarrow {a_{n + 1}} = \frac{1}{2}({a_n} + \frac{3}{{{a_n}}})\;\;\:;\;\;\:{a_1} = 3\\\\{a_2} = \frac{1}{2}({a_1} + \frac{3}{{{a_1}}}) = \frac{1}{2}(3 + \frac{3}{3}) = \frac{1}{2}(3 + 1) = 2\\\\{a_3} = \frac{1}{2}({a_2} + \frac{3}{{{a_2}}}) = \frac{1}{2}(2 + \frac{3}{2})\\\\ = \frac{1}{2} \times \frac{7}{2} = \frac{7}{4} \simeq 1/75\end{array}\)
ج
\(\begin{array}{l} \Rightarrow {a_{n + 1}} = \frac{1}{2}({a_n} + \frac{5}{{{a_n}}})\;\;\:;\;\;\:{a_1} = 5\\\\{a_2} = \frac{1}{2}({a_1} + \frac{5}{{{a_1}}}) = \frac{1}{2}(5 + \frac{5}{5}) = \frac{1}{2}(5 + 1) = 3\\\\{a_3} = \frac{1}{2}({a_2} + \frac{5}{{{a_2}}}) = \frac{1}{2}(3 + \frac{5}{3})\\\\ = \frac{1}{2} \times \frac{{14}}{3} = \frac{{14}}{6} = \frac{7}{3} \simeq 2/33\end{array}\)
مزیت این روش این است که در صورت عدم دسترسی به ماشین حساب، می توان به راحتی محاسبه مقدار تقریبی ریشه دوم اعداد طبیعی را تعیین کرد.
11 جملات دنبالهٔ بازگشتی \({a_{n + 1}} = {a_n} + \left( {n + 1} \right)\;,\;{a_1} = 1\) رأس کدام یک از الگوهای زیر را مشخص می کنند؟

\(\begin{array}{*{20}{l}}\begin{array}{l}{a_{n + 1}} = {a_n} + (n + 1)\;\;\:,\;\;\:{a_1} = 1\;\;\:\\\\ \Rightarrow \;\;\:\left\{ {\begin{array}{*{20}{l}}{{a_1} = 1}\\{n = 1 \to {a_2} = {a_1} + (1 + 1) = 1 + 2 = 3}\\{n = 2 \to {a_3} = {a_2} + (2 + 1) = 3 + 3 = 6}\end{array}} \right.\end{array}\\{}\\{{a_n}:\;\:1\;\:,\;\:3\;\:,\;\:6\;\;,\;\: \cdots }\end{array}\)
این دنباله با جملات الگوی الف مطابقت دارد.
12 مطابق گزارش سازمان محیط زیست، به دلیل ورود پسَ ماندهای صنعتی کارخانه ها به یک دریاچه، 250 تن فاضلاب صنعتی به این دریاچه وارد شده است. محیط زیست دریاچه سالیانه 10 % فاضلاب صنعتی را به صورت طبیعی خنثی و بی اثر می کند. سازمان محیط زیست با وضع قوانین جدید میزان ورودی فاضلاب صنعتی به دریاچه را به 15 تن در سال کاهش داده است.
اگر P1=250 میزان آلودگی فعلی دریاچه باشد، با نوشتن یک رابطهٔ بازگشتی، میزان مواد آلودهٔ صنعتی را بعد از دو سال و پنج سال محاسبه کنید.
\(\begin{array}{l}{p_{n + 1}} = {p_n} - \frac{1}{{10}}{p_n} - 15\\\\ \Rightarrow {p_{n + 1}} = \frac{9}{{10}}{p_n} - 15\quad ,\quad {p_1} = 250\end{array}\)
پایان سال اول:
\(n = 1 \to {p_2} = \frac{9}{{10}}{p_1} - 15 = \frac{9}{{10}} \times 250 - 15 = 210\)
پایان سال دوم:
\(n = 2 \to {p_3} = \frac{9}{{10}}{p_2} - 15 = \frac{9}{{10}} \times 210 - 15 = 174\)
پایان سال سوم:
\(n = 3 \to {p_4} = \frac{9}{{10}}{p_3} - 15 = \frac{9}{{10}} \times 174 - 15 = 141/6\)
پایان سال چهارم:
\(n = 4 \to {p_5} = \frac{9}{{10}}{p_4} - 15 = \frac{9}{{10}} \times 141/6 - 15 = 112/44\)
پایان سال پنجم:
\(n = 5 \to {p_6} = \frac{9}{{10}}{p_5} - 15 = \frac{9}{{10}} \times 112/44 - 15 = 86/156\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















