جواب فعالیت صفحه 90 درس 3 ریاضی و آمار دوازدهم انسانی (الگوهای غیر خطی)

1 پدر محمد زیست شناس است و در آزمایشگاه روی باکتری ها کار می کند. روزی او محمد را با خود به محل کارش برد و نوعی باکتری را در زیر میکروسکوپ، نشانش داد که در شرایط آزمایشگاهی در هر ساعت جرم آن 2 برابر می شود. سپس، از محمد خواست که جرم اولیهٔ باکتری را یک گرم در نظر بگیرد و جدول زیر را کامل کند. شما نیز به او در کامل کردن جدول کمک کنید.

محمد پس از کامل کردن جدول، از پدرش پرسید: آیا حتماً باید تا پایان ساعت منتظر شویم و نمی توانیم جرم باکتری را در کمتر از یک ساعت به دست آوریم؟ برای مثال، جرم باکتری ها پس از نیم ساعت چقدر می شود؟

پدر محمد: نظر خودت دربارهٔ جرم باکتری ها پس از نیم ساعت چیست؟

محمد: مطمئن نیستم ولی حدس می زنم که \({2^{\frac{1}{2}}}\) گرم شود، اما مقدار \({2^{\frac{1}{2}}}\) را نمی دانم چقدر می شود؛ چون تمام توان هایی که ما تاکنون یاد گرفته ایم، توان های صحیح بوده اند.

پدر محمد به صورت زیر به او نشان داد که جرم باکتری ها پس از نیم ساعت چقدر می شود و او را با توان های گویا آشنا کرد:

پس، جرم باکتری ها بعد از نیم ساعت (\(\frac{1}{2}\) ساعت)، \({2^{\frac{1}{2}}}\) گرم خواهد بود و حدس شما درست است. حالا بعد از پانزده دقیقه، جرم باکتری ها چند گرم خواهد شد؟

محمد: چون پانزده دقیقه، \(\frac{1}{4}\) ساعت است، پس \({2^{\frac{1}{4}}}\) گرم یا \(\sqrt[4]{2}\) گرم خواهد بود.

حالا شما مانند محمد جرم باکتری ها را در زمان های داده شده به دست آورید.

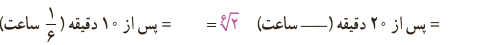
در این کتاب اگر \({a^{\frac{1}{n}}}\;\;,\;\;a < 0\) را تعریف نمی کنیم. برای مثال، عبارت هایی مانند \({\left( { - 1} \right)^{\frac{1}{3}}}\;,\;{\left( { - 2} \right)^{\frac{1}{2}}}\) را تعریف نمی کنیم. همچنین، هرجا عبارت های \({a^{\frac{1}{n}}}\) ، a را عددی مثبت در نظر می گیریم.

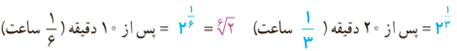
2 در خصوص توان های صحیح اعداد دیدید که: \({2^6} = {2^{2 \times 3}} = {\left( {{2^2}} \right)^3}\)

دربارهٔ توان های گویای اعداد نیز می توانیم به طریقی مشابه عمل کنیم:

\(\begin{array}{l}{3^{\frac{2}{3}}} = {3^{2 \times \frac{1}{3}}} = {\left( {{3^2}} \right)^{\frac{1}{3}}} = \sqrt[3]{{{3^2}}}\\\\{7^{\frac{5}{4}}} = {7^{5 \times \frac{1}{4}}} = {\left( {{7^5}} \right)^{\frac{1}{4}}} = \sqrt[4]{{{7^5}}}\end{array}\)

اعداد توان دار زیر را به شکل رادیکالی بنویسید.

\(\begin{array}{l}{5^{\frac{3}{4}}} = \\\\{6^{\frac{7}{9}}} = \\\\{12^{ - \frac{2}{{11}}}} = \\\\{\left( {2\frac{1}{3}} \right)^{ - \frac{8}{3}}} = \\\\{\left( {0/001} \right)^{\frac{{14}}{4}}} = \end{array}\)