دانلود اپلیکیشن
برای درمان شخصی که مبتلا به نوعی گلودرد عفونی است، پزشک معالج قرص های آنتی بیوتیک حامل 80 میلی گرم آنتی بیوتیک تجویز کرد. با توجه به اینکه نیمه عمر این آنتی بیوتیک هشت ساعت است، شخص بیمار باید در پایان هر هشت ساعت پس از خوردن قرص پیشین، این قرص ها را مصرف کند.
الف با کامل کردن جدول زیر، میزان آنتی بیوتیک موجود در بدن شخص بیمار را پس از سه و شش بار مصرف قرص مشخص کنید.
ب با یک «رابطه بازگشتی» میزان آنتی بیوتیک در بدن شخص بیمار را پس از n بار مصرف قرص مشخص کنید.
ج آیا می توانید میان تعداد قرص مصرفی و میزان آنتی بیوتیک موجود در بدن شخص بیمار رابطه ای مشخص کنید؟ (ضابطهٔ تابعی دنباله)
الف اگر «Sn» میزان آنتی بیوتیک موجود در بدن شخص بیمار پس از n بار مصرف قرص باشد، با توجه به فرض های مسئله:
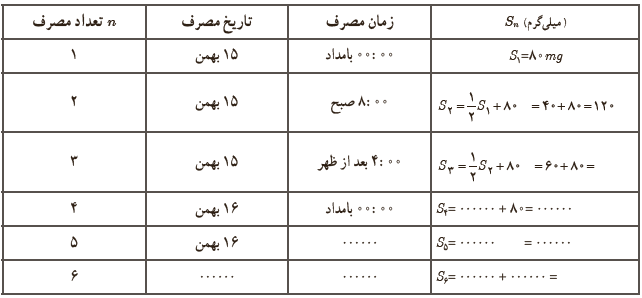
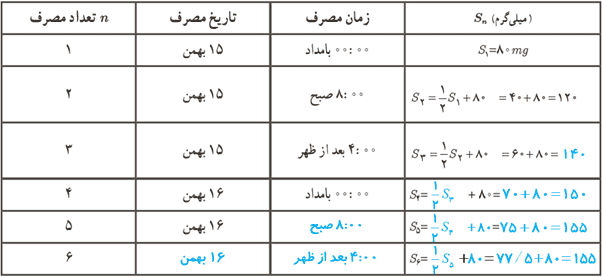
ب با توجه به نحوهٔ کامل کردن جدول بالا، رابطهٔ بازگشتی میزان آنتی بیوتیک در بدن شخص پس از n بار مصرف دارو از رابطهٔ زیر مشخص می شود:
\({S_{n + 1}} = \;..........\; + \frac{1}{2}{S_n}\;\;\;,\;\;{S_1} = .......\)
\({S_{n + 1}} = \;80\; + \frac{1}{2}{S_n}\;\;\;,\;\;{S_1} = 80\)
ج برای نوشتن ضابطهٔ تابعی دنبالهٔ Sn بر حسب n، اگر میزان آنتی بیوتیک هر قرص را A میلی گرم در نظر بگیریم (در این مسئله A=80mg است)، با استفاده از رابطهٔ بازگشتی به دست آمده در قسمت ب:
\(\begin{array}{l}{S_1} = A\\\\{S_2} = A + \frac{1}{2}{S_1} = ....\\\\{S_3} = ....\; + \;.... = A + \frac{1}{2}\left( {A + \frac{1}{2}A} \right) = A + \frac{1}{2}A + {\left( {\frac{1}{2}} \right)^2}A\end{array}\)
به همین صورت برای محاسبهٔ S6 :
\({S_6} = A + \frac{1}{2}A + {\left( {\frac{1}{2}} \right)^2}A + ....\; + {\left( {\frac{1}{2}} \right)^{...}}A\)
پس برای محاسبهٔ مجموع آنتی بیوتیک در بدن شخص پس از n بار مصرف:
\({S_n} = A + \frac{1}{2}A + {\left( {\frac{1}{2}} \right)^2}A + ....\; + {\left( {\frac{1}{2}} \right)^{.n - 1}}A\;\;\;(1)\)
اگر طرفین رابطه (1) را در ضریب \(\frac{1}{2}\) ضرب کنیم:
\(\frac{1}{2}{S_n} = \frac{1}{2}A + \;....\; + \;....\; + \;....\;\;\;(2)\)
با تفاضل رابطهٔ (1) از (2) رابطهٔ زیر به دست می آید:
\(\begin{array}{l}{S_n} - \frac{1}{2}{S_n} = A - {\left( {\frac{1}{2}} \right)^n}A\;\;\\\\ \Rightarrow \;\;{S_n}\left( {1 - \frac{1}{2}} \right) = A\left( {1 - {{\left( {\frac{1}{2}} \right)}^n}} \right)\\\\ \Rightarrow \;{S_n} = A \times \frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{1 - \frac{1}{2}}}\;\;\\\\ \Rightarrow \;{S_n} = 2A\left( {1 - {{\left( {\frac{1}{2}} \right)}^n}} \right)\end{array}\)
بنابراین، با فرض این مسئله A=80mg مجموع میزان آنتی بیوتیک پس از n بار مصرف:
\({S_n} = 160\left( {1 - {{\left( {\frac{1}{2}} \right)}^n}} \right)\)
\(\begin{array}{l}{S_1} = A\\\\{S_2} = A + \frac{1}{2}{S_1} = A + \frac{1}{2}A\\\\{S_3} = A + \frac{1}{2}{S_2} = A + \frac{1}{2}\left( {A + \frac{1}{2}A} \right)\\\\ = A + \frac{1}{2}A + {\left( {\frac{1}{2}} \right)^2}A\end{array}\)
اگر طرفین رابطه (1) را در ضریب \(\frac{1}{2}\) ضرب کنیم:
\(\frac{1}{2}{S_n} = \frac{1}{2}A + \;{(\frac{1}{2})^2}A + \;....\; + \;{(\frac{1}{2})^{n - 1}}A\;\;\;(2)\)
د با توجه به رابطهٔ به دست آمده برای Sn :
\(\begin{array}{l}{S_1} = 160\left( {1 - {{\left( {\frac{1}{2}} \right)}^1}} \right) = 160 \times \frac{1}{2} = 80\\\\{S_2} = ..........\\\\{S_3} = ..........\end{array}\)
\(\begin{array}{l}{S_1} = 160\,(1 - {(\frac{1}{2})^1}) = 160 \times \frac{1}{2} = 80\\\\{S_2} = 160\,(1 - {(\frac{1}{2})^2}) = 160 \times \frac{3}{4} = 120\\\\{S_3} = 160\,(1 - {(\frac{1}{2})^6}) = 160 \times \frac{{63}}{{64}} = \frac{{315}}{2} = 157/5\end{array}\)
1736019749.png)
