آیا تمام سوالات کار در کلاس صفحه 61 ریاضی نهم، مطابق با آخرین تغییرات کتب درسی پاسخ داده شده است ؟

بله، تمام جواب ها به کار در کلاس صفحه 61 ریاضی نهم مطابق با آخرین تغییرات کتب درسی 1402 - 1401 است.

آیا جواب ها به صورت آموزش محور و کامل بیان شده اند ؟

بله، جواب سوالات به صورت کاملا تشریحی و با هدف یادگیری و تسلط به مبحث بیان شده اند.

جواب کار در کلاس صفحه 61 درس 4 ریاضی نهم (توان و ریشه)

تعداد بازدید : 84.74M

پاسخ کار در کلاس صفحه 61 ریاضی نهم

گام به گام کار در کلاس صفحه 61 درس توان و ریشه

کار در کلاس صفحه 61 درس 4

شما در حال مشاهده جواب کار در کلاس صفحه 61 ریاضی نهم هستید. ما در تیم مای درس، پاسخ‌نامه‌های کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کرده‌ایم. اگر به دنبال به‌روزترین پاسخ‌ها برای این صفحه هستید و می‌خواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخ‌های گام به گام، به گنجینه‌ای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مای‌درس را نصب نمایید.

📥 دانلود اپلیکیشن مای‌درس

برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینه‌ای از گام‌به‌گام‌ها و نمونه سوالات، اپلیکیشن را نصب کنید.

نصب رایگان اپلیکیشن

1 با توجه به مثال های حل شده زیر، پاسخ موارد بعدی را به صورت یک عدد توان دار با توان طبیعی بنویسید:

الف \({5^{ - 2}} = \frac{1}{{{5^2}}} = \frac{1}{{25}} = {\left( {\frac{1}{5}} \right)^2}\)

ب \({\left( {\frac{2}{3}} \right)^{ - 2}} = \frac{1}{{{{\left( {\frac{2}{3}} \right)}^2}}} = \frac{1}{{\frac{4}{9}}} = \frac{9}{4} = {\left( {\frac{3}{2}} \right)^2}\)

ج \({\left( { - 6} \right)^{ - 3}} = \frac{1}{{\,\,\,\,\,\,\,}} = \frac{{\,\,\,\,\,\,\,}}{{\,\,\,\,\,\,\,}} = \)

د \({\left( { - \frac{2}{7}} \right)^{ - 4}} = \,\,\,\,\,\,\, = \,\,\,\,\,\, = \)

ج \({\left( { - 6} \right)^{ - 3}} = \frac{1}{{{{\left( { - 6} \right)}^{ - 3}}}} = \frac{1}{{108}} = - \frac{1}{{{6^3}}}\)

د \({\left( { - \frac{2}{7}} \right)^{ - 4}} = \frac{1}{{{{\left( { - \frac{2}{7}} \right)}^4}}} = \frac{1}{{\frac{8}{{2401}}}} = \frac{{2401}}{8} = {\left( { - \frac{7}{2}} \right)^4}\)

2 عبارت های برابر را مانند نمونه به هم وصل کنید : \(\left( {x \ne 0,y \ne 0} \right)\)

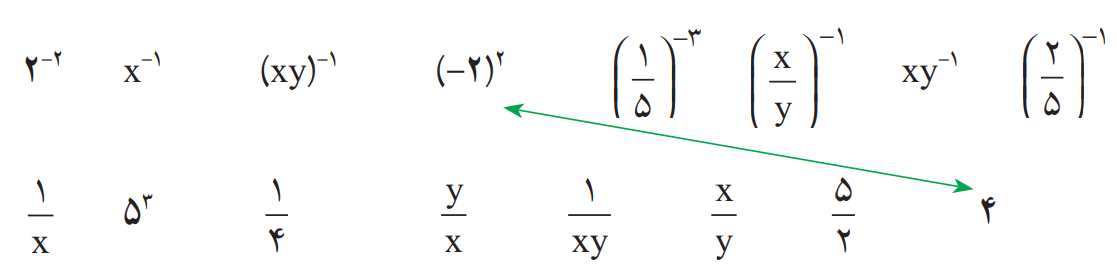
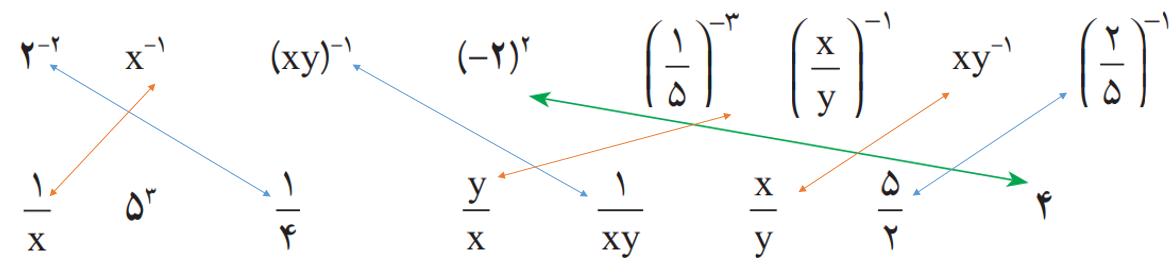
3 حاصل هر عبارت را به ساده ترین صورت بنویسید :

الف \({\left( { - \frac{1}{3}} \right)^{ - 4}} = \)

ب \({2^{ - 1}} + {3^{ - 1}} + {4^{ - 1}} = \)

ج \( - {\left( { - 5} \right)^2} = \)

د \( - {\left( { - 5} \right)^{ - 2}} = \)

هـ \( - {5^{ - 2}} = \)

و \({1^{ - 2}} = \)

ز \(\frac{{{{\left( { - 3} \right)}^0}}}{3} = \)

ح \( - \frac{1}{{{2^{ - 2}}}} = \)

ط \({\left( {\frac{2}{5}} \right)^{ - 2}} + {\left( {\frac{5}{2}} \right)^2} = \)

ی \({2^0} - {2^{ - 1}} = \)

الف \({\left( { - \frac{1}{3}} \right)^{ - 4}} = {\left( { - 3} \right)^4} = 81\)

ب \({2^{ - 1}} + {3^{ - 1}} + {4^{ - 1}} = \frac{1}{2} + \frac{1}{3} + \frac{1}{4} = \frac{{6 + 4 + 3}}{{12}} = \frac{{13}}{{12}}\)

ج \( - {\left( { - 5} \right)^2} = - \left( { + 25} \right) = - 25\)

د \( - {\left( { - 5} \right)^{ - 2}} = - {\left( { - \frac{1}{5}} \right)^2} = - \frac{1}{{25}}\)

هـ \( - {5^{ - 2}} = - {\left( {\frac{1}{5}} \right)^2} = - \frac{1}{{25}}\)

و \({1^{ - 2}} = \frac{1}{{{1^2}}} = 1\)

ز \(\frac{{{{\left( { - 3} \right)}^0}}}{3} = \frac{1}{3}\)

ح \( - \frac{1}{{{2^{ - 2}}}} = \frac{1}{{{{\left( {\frac{1}{2}} \right)}^2}}} = 4\)

ط \({\left( {\frac{2}{5}} \right)^{ - 2}} + {\left( {\frac{5}{2}} \right)^2} = {\left( {\frac{5}{2}} \right)^2} + {\left( {\frac{5}{2}} \right)^2} = \frac{{25}}{4} + \frac{{25}}{4} = \frac{{50}}{4}\)

ی \({2^0} - {2^{ - 1}} = 1 - \frac{1}{2} = \frac{1}{2}\)