دانلود اپلیکیشن
فرض و حکم را برای مسئله های زیر مشخص کنید:
1 در دو مثلث داده شده زوایای برابر در شکل مشخص شده است. ثابت کنید زاویه های سوم از دو مثلث نیز با هم برابر است.
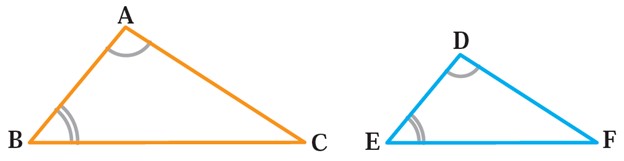
\(\begin{array}{l} \cdots = \cdots \\\\ \cdots = \cdots \end{array}\)فرض:
\( \cdots = \cdots \)حکم:
\(\begin{array}{l}\hat A = \hat D\\\\\hat B = \hat E\end{array}\)فرض:
\(\begin{array}{l} \Rightarrow \hat A + \hat B = \hat D + \hat E\\\\ \Rightarrow {180^ \circ } - (\hat A + \hat B) = {180^ \circ } - (\hat D + \hat E)\end{array}\)
می دانیم مجموع زاویه های هر مثلث برابر 180 درجه است:
\(\begin{array}{l}{180^ \circ } - (\hat A + \hat B) = \hat C\\\\{180^ \circ } - (\hat D + \hat E) = \hat F\end{array}\)
\( \Rightarrow \hat C = \hat F\)حکم:
2 اگر در یک مثلث دو زاویه نابرابر باشد، ضلع روبه رو به زاویهٔ بزرگ تر، بزرگ تر است از، ضلع روبه رو به زاویهٔ کوچک تر. (ابتدا شکل را رسم کرده و نام گذاری کنید).
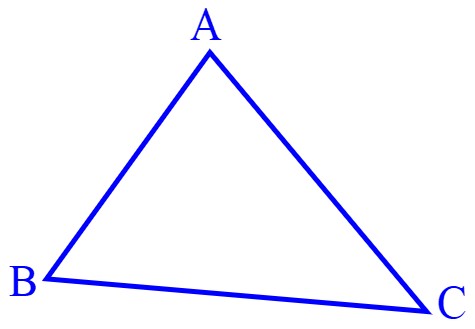
\(AC > AB\)فرض:
\(\hat B > \hat C\)حکم:
روی ضلع بزرگتر یعنی AC به اندازه ی AB جدا می کنیم:
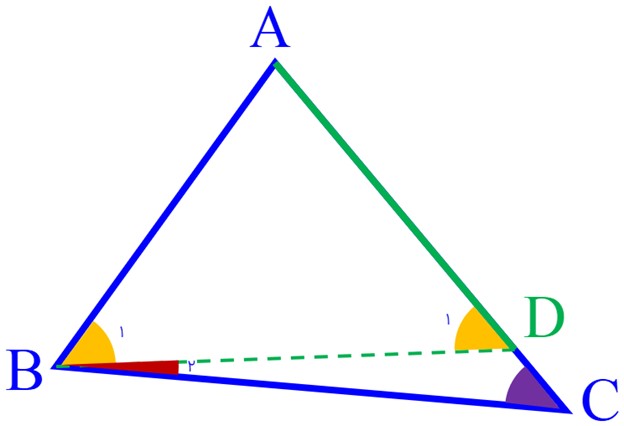
چون AB = AD می باشد، داریم:
\(AB = AD \Rightarrow {\hat B_1} = {\hat D_1}\)
همچنین در مثلث BDC داریم:
\(B\mathop D\limits^\Delta C:\,\,\,\,\,{\hat D_1} = {\hat B_2} + \hat C\)
نتیجه می شود:
\(\begin{array}{l}\left. \begin{array}{l}{{\hat B}_1} = {{\hat D}_1}\\\\{{\hat D}_1} = {{\hat B}_2} + \hat C\end{array} \right\} \Rightarrow {{\hat B}_1} = {{\hat B}_2} + \hat C\\\\\left. \begin{array}{l} \Rightarrow {{\hat B}_1} > \hat C\\\\\hat B = {{\hat B}_1} + {{\hat B}_2}\end{array} \right\} \Rightarrow \hat B > \hat C\end{array}\)
بنابراین با داشتن فرض AC > AB چنین نتیجه گرفتیم که \(\hat B > \hat C\)
عکس قضیۀ بالا:
\(\hat B > \hat C\) فرض:
\(AC > AB\)حکم:
برهان خلف:
اگر AC = AB باشد، آن گاه داریم \(\hat B = \hat C\)
اگر AC < AB باشد، آن گاه طبق قضیۀ بالا داریم که \(\hat B < \hat C\)
بنابراین چون دو حالت دیگر به هیچ عنوان رخ نمی دهد و فرض مسئله این است که \(\hat B > \hat C\) ، تنها حکمی که رخ خواهد داد این است که \(AC > AB\)
3 نشان دهید در هر مثلث اندازهٔ هر زاویه خارجی با مجموع دو زاویهٔ داخلی غیرمجاور آن برابر است.
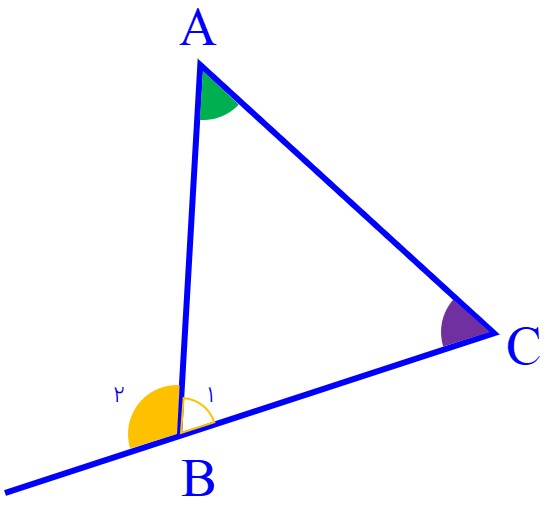
\({\hat B_2} = \hat A + \hat C\)
می دانیم که در هر مثلث، مجموع زوایای داخلی برابر با 180 درجه می شود:
\({\hat B_1} + \hat A + \hat C = {180^ \circ }\,\,\,\,\,\,\,\,\,\,(1)\)
همچنین می دانیم که بر روی امتداد پاره خط BC در رأس B، چنین داریم:
\({\hat B_1} + {\hat B_2} = {180^ \circ }\,\,\,\,\,\,\,\,\,\,(2)\)
از عبارت های (1) و (2) چنین نتیجه می گیریم که:
\(\begin{array}{l}\mathop \Rightarrow \limits^{(1)\,\,\,\,\,,\,\,\,\,\,(2)} \left\{ \begin{array}{l}{{\hat B}_1} + \hat A + \hat C = {180^ \circ }\\\\{{\hat B}_1} + {{\hat B}_2} = {180^ \circ }\end{array} \right.\\\\ \Rightarrow \left\{ \begin{array}{l}\hat A + \hat C = {180^ \circ } - {{\hat B}_1}\\\\{{\hat B}_2} = {180^ \circ } - {{\hat B}_1}\end{array} \right.\\\\ \Rightarrow {{\hat B}_2} = \hat A + \hat C\end{array}\)
1736019749.png)
