1736019749.png)
جواب کار در کلاس صفحه 40 درس 3 ریاضی نهم (استدلال و اثبات در هندسه)
تعداد بازدید : 78.8Mپاسخ کار در کلاس صفحه 40 ریاضی نهم
-گام به گام کار در کلاس صفحه 40 درس استدلال و اثبات در هندسه
-کار در کلاس صفحه 40 درس 3
-شما در حال مشاهده جواب کار در کلاس صفحه 40 ریاضی نهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
به استدلال هایی دقت کنید که چهار دانش آموز برای مسئلهٔ زیر آورده اند:
مسئله: مجموع زاویه های داخلی مثلث \({180^ \circ }\) است.
استدلال حامد: حامد گفت یک مثلث متساوی الاضلاع را درنظر می گیریم؛ چون سه زاویه دارد و هر زاویه \({60^ \circ }\) است، مجموع زاویه های مثلث \({180^ \circ }\) است.
استدلال حسین: حسین چند مثلث مختلف با حالت های گوناگون کشید و زوایای آنها را اندازه گرفت و دید که در همهٔ آنها مجموع زوایای داخلی برابر \({180^ \circ }\) است و نتیجه گرفت که مجموع زوایای داخلی هر مثلث \({180^ \circ }\) است.
استدلال مهدی: مهدی شکل روبرو را، که از مثلث های هم نهشت تشکیل شده است کشید و با مشخص کردن زاویه های مثلث ABC مانند شکل استدلالی با استفاده از شکل به صورت زیر آورد:
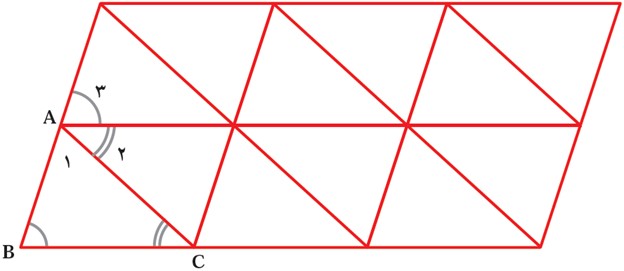
\({\hat A_1} + \hat B + \hat C = {\hat A_1} + {\hat A_3} + {\hat A_2} = {180^ \circ }\)
استدلال رضا: رضا گفت می دانیم که «هر خطی که دو خط موازی را قطع کند، با آنها هشت زاویه می سازد که مانند شکل چهار به چهار با هم مساوی اند».
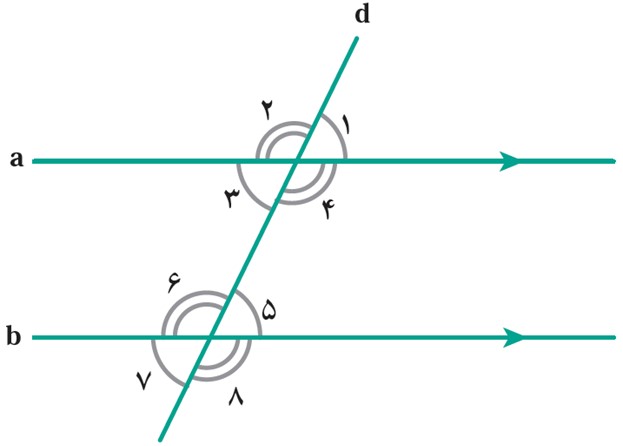
حال مثلثی دلخواه مانند \(A\mathop B\limits^\Delta C\) را درنظر می گیریم؛ مانند شکل مقابل از رأس A خط d را موازی BC رسم می کنیم. سه زاویهٔ تشکیل شده در رأس A را با شماره های 1، 2 و 3 نشان داده ایم که زاویۀ A2 همان زاویۀ A در مثلث است و با درنظر گرفتن AB به عنوان مورّب داریم: \(\hat C = {\hat A_3}\) پس با جای گذاری \({\hat A_1}\) و \({\hat A_3}\) به ترتیب به جای \(\hat B\) و \(\hat C\) خواهیم داشت: \(\hat A + \hat B + \hat C = {\hat A_2} + {\hat A_1} + {\hat A_3} = {180^ \circ }\)
استدلال رضا را می توان با استفاده از نمادهای ریاضی مرتبّ و خلاصه کرد و بدین صورت نوشت:
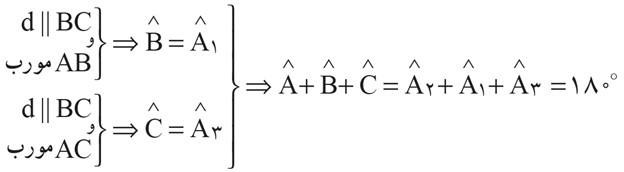
دربارهٔ معتبر بودن استدلال های این دانش آموزان بحث کنید.
1 نقد استدلال حامد:
روش حامد:
او فقط یک نوع خاص از مثلث (متساویالاضلاع) را انتخاب کرد و دید که مجموع زاویههایش ۱۸۰ درجه است.
تحلیل:
استدلال حامد کامل نیست.
چرا؟
او از روش «مثال زدن» استفاده کرده است. اینکه قانون برای یک مثلث خاص (مثلث متساویالاضلاع) درست است، دلیل نمیشود که برای هزاران مدل مثلث دیگر (مثل قائمالزاویه یا مختلفالاضلاع) هم درست باشد. ما در ریاضی با یک مثال نمیتوانیم قانون کلی صادر کنیم.
2 نقد استدلال حسین:
روش حسین:
او تعداد زیادی مثلث مختلف کشید و با نقاله اندازهگیری کرد.
تحلیل:
استدلال حسین هم اثبات ریاضی محسوب نمیشود.
چرا؟
1 خطای اندازهگیری: همانطور که قبلاً گفتیم، ابزارهای اندازهگیری و چشم انسان خطا دارند. ممکن است مجموع زاویهها ۱۷۹ یا ۱۸۱ درجه شود و او گرد کرده باشد.
2 ناتوانی در بررسی همه موارد: حسین هر چقدر هم تلاش کند، نمیتواند تمام مثلثهای دنیا را رسم و اندازه بگیرد. همیشه ممکن است مثلثی باشد که او بررسی نکرده است.
3 نقد استدلال مهدی:
روش مهدی:
او از خاصیت «کاشیکاری» یا کنار هم چیدن مثلثهای همنهشت استفاده کرده است.
تحلیل:
استدلال مهدی بسیار هوشمندانهتر و معتبرتر از دو نفر قبلی است.
چرا؟
او نشان داد که اگر سه مثلث همنهشت (دقیقاً مثل هم) را کنار هم بچینیم، زاویههای مختلف آنها (مثلاً زاویههای ۱، ۲ و ۳ در شکل) در کنار هم یک خط راست (نیمصفحه) میسازند.
چون زاویه نیمصفحه ۱۸۰ درجه است، پس نشان میدهد که مجموع این سه زاویه (که همان زاویههای داخلی مثلث هستند) برابر با ۱۸۰ درجه میشود.
این روش یک «استدلال شهودی» قوی است که به اثبات ریاضی بسیار نزدیک است، اما دقیق نیست، چون بر اساس ویژگیهای شکل است نه اندازهگیری عددی.
4 بررسی استدلال رضا (بهترین و کاملترین اثبات):
روش:
رضا از اصول هندسی (خطوط موازی و مورب) استفاده کرد که برای همه مثلثها صادق است.
نقد:
استدلال رضا کاملاً معتبر و یک اثبات ریاضی دقیق است.
چرا؟
او از خط d موازی با BC استفاده کرد.
طبق قانون خطوط موازی و مورب، زاویه \(\hat B\) با \({\hat A_1}\) برابر شد و زاویه \(\hat C\) با \({\hat A_3}\) برابر شد.
چون مجموع زاویههای روی خط راست در راس A برابر 180 است \(({\hat A_1} + {\hat A_2} + {\hat A_3} = {180^ \circ })\) ، پس مجموع زاویههای داخل مثلث \((\hat B + \hat A + \hat C)\) هم حتماً ۱۸۰ درجه است.
نتیجهگیری نهایی
استدلال رضا تنها استدلال کاملاً معتبر ریاضی است، زیرا به نوع مثلث یا اندازهگیری وابسته نیست و بر اساس اصول اثباتشده (قضیه خطوط موازی) بنا شده است. روش مهدی هم به عنوان یک استدلال شهودی ارزشمند است، اما روش حامد و حسین در اثبات ریاضی جایی ندارند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
