آیا تمام سوالات فعّالیت صفحه 39 ریاضی نهم، مطابق با آخرین تغییرات کتب درسی پاسخ داده شده است ؟

بله، تمام جواب ها به فعّالیت صفحه 39 ریاضی نهم مطابق با آخرین تغییرات کتب درسی 1402 - 1401 است.

آیا جواب ها به صورت آموزش محور و کامل بیان شده اند ؟

بله، جواب سوالات به صورت کاملا تشریحی و با هدف یادگیری و تسلط به مبحث بیان شده اند.

جواب فعّالیت صفحه 39 درس 3 ریاضی نهم (استدلال و اثبات در هندسه)

تعداد بازدید : 78.78M

پاسخ فعّالیت صفحه 39 ریاضی نهم

گام به گام فعّالیت صفحه 39 درس استدلال و اثبات در هندسه

فعّالیت صفحه 39 درس 3

شما در حال مشاهده جواب فعّالیت صفحه 39 ریاضی نهم هستید. ما در تیم مای درس، پاسخ‌نامه‌های کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کرده‌ایم. اگر به دنبال به‌روزترین پاسخ‌ها برای این صفحه هستید و می‌خواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخ‌های گام به گام، به گنجینه‌ای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مای‌درس را نصب نمایید.

1 در مسئلهٔ زیر، فرض و حکم را بنویسید و اشکال استدلال داده شده را بیابید، سپس استدلال درستی برای آن بنویسید.

مسئله: در شکل مقابل پاره خط AC نیمساز زاویۀ A است و اضلاع AB و AD برابرند. ثابت کنید مثلث های مثلث \(A\mathop B\limits^\Delta C\) و \(A\mathop D\limits^\Delta C\) هم نهشت اند.

: فرض

: حکم

استدلال: چون AC نیمساز است، داریم \({\hat A_1} = {\hat A_2}\) و \({\hat C_1} = {\hat C_2}\) و از طرفی AC نیز ضلع مشترک در هر دو مثلث است، لذا دو مثلث ABC و ADC به حالت دو زاویه و ضلع بین (ز ض ز) هم نهشت اند.

پاره خط AC نیمساز زاویۀ A است و اضلاع AB و AD برابرند : فرض

\(A\mathop B\limits^\Delta C \cong A\mathop D\limits^\Delta C\) :حکم

اشکال استدلال:

AC نیمساز زاویه A است نه زاویه C در نتیجه ممکن است که \(.\,\,{\hat C_1} \ne {\hat C_2}\)

استدلال:

AC نیمساز زاویه A است بنابراین \({\hat A_1} = {\hat A_2}\) و همچنین AC ضلع مشترک در هر دو مثلث است و طبق فرض مسئله AD = AB می باشد بنابراین دو مثلث \(A\mathop B\limits^\Delta C\) و \(A\mathop D\limits^\Delta C\) به حالت دو ضلع و زاویه بین (ض ز ض) هم نهشت اند.

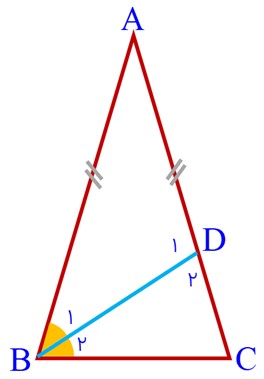
2 مثلث زیر متساوی الساقین و AD نیمساز وارد بر قاعدهٔ آن است. با استدلال زیر نشان داده ایم که نیمساز وارد بر قاعده، میانه نیز می باشد.

لذا نقطهٔ D وسط BC است و AD میانه است.

آیا در مثلث ABC می توان نتیجه گرفت که نیمساز زاویۀ B نیز میانهٔ ضلع مقابل آن است؟ به عبارتی، آیا می توان خاصیت اثبات شده برای نیمساز A را به نیمساز دیگر تعمیم داد؟

خیر، نمی‌توانیم چنین نتیجه‌ای بگیریم.

بیایید با هم دلیل آن را دقیق و موشکافانه بررسی کنیم:

1 چرا اثبات برای زاویه A درست بود؟

در اثبات بالا که برای نیمساز زاویه A نوشته شده، از خاصیت «برابری ساق‌ها» (AB = AC) استفاده شده است. چون زاویه A دقیقاً بین دو ساق برابر قرار دارد، شرط هم‌نهشتی (ض ز ض) برقرار شد و توانستیم ثابت کنیم نیمساز، میانه هم هست.

2 چرا برای زاویه B درست نیست؟

حالا بیایید به سراغ زاویه B برویم. اضلاع تشکیل‌دهندهٔ زاویه B، یکی ساق AB است و دیگری قاعدۀ BC.

در یک مثلث متساوی‌الساقین معمولی، ساق با قاعده برابر نیست \(.(AB \ne BC)\)
بنابراین، اگر بخواهیم نیمساز زاویه B را رسم کنیم، دیگر آن دو ضلعِ کناریِ زاویه با هم برابر نیستند و نمی‌توانیم از همان استدلال قبلی (ض ز ض) استفاده کنیم.

3 تصور ذهنی (شهود هندسی):

یک مثلث متساوی‌الساقین خیلی بلند و باریک را تصور کن (مثل کلاه بوقی). اگر نیمساز یکی از زاویه‌های پایین (قاعده) را بکشی، می‌بینی که ضلع روبه‌رو را در جایی نزدیک به پایین قطع می‌کند، نه دقیقاً در وسط آن.

نتیجه‌گیری مهم آموزشی

در مثلث متساوی‌الساقین، زاویه رأس (A) ویژگی‌های منحصر‌به‌فردی دارد که با زاویه‌های قاعده (B و C) متفاوت است. ما در ریاضیات فقط زمانی می‌توانیم یک خاصیت را «تعمیم» دهیم که شرایط برای همه موارد یکسان باشد. (این خاصیت فقط در مثلث متساوی‌الاضلاع برای همه زاویه‌ها صادق است، چون همه اضلاع با هم برابرند).

3 با استدلال زیر به سادگی می توان نتیجه گیری کرد که قطر AC از مربع ABCD نیمساز زاویه های A و C است. چون دو مثلث ABC و ADC به حالت سه ضلع هم نهشت اند و زوایای متناظر با هم برابرند؛ بنابراین \({\hat A_1} = {\hat A_2}\) و \({\hat C_1} = {\hat C_2}\) و لذا AC نیمساز است.

آیا می توان با استدلالی مشابه، این خاصیت را به قطر دیگر نیز تعمیم داد و گفت به طور کلی در مربع هر قطر نیمساز زاویه های دو سر آن قطر است؟

AC نیم ساز زاویه های A و C می باشد.

بله؛ می توان به طور کلی گفت که در هر مربع، هر قطر نیمساز زاویه های دو سر آن قطر است.

4 به نظر شما چرا در فعالیت 2 خاصیت موردنظر قابل تعمیم به نیمسازهای دیگر نبود؛ اما در فعالیت 3 خاصیت موردنظر به قطر دیگر تعمیم داده می شود؟

در فعالیت 2، با عوض شدن نیمساز شرایط متفاوت بوجود می آید و نمی توان میانه بودن را ثابت کرد ولی در فعالیت 3، وقتی قطر عوض می شود شرایط تغییری نمی کند.

وقتی خاصیتی را برای یک عضو از یک مجموعه ثابت کردیم، اگر تمام ویژگی هایی که در استدلال خود به کار برده ایم، در سایر عضوهای آن مجموعه نیز باشد، می توان درستی نتیجه را به همهٔ عضوهای آن مجموعه تعمیم داد.

5 نقطه ای مانند P، روی عمودمنصف پاره AB در نظر می گیریم و به دو سر پاره خط وصل می کنیم. چون دو مثلث AHP و BHP به حالت (ض ز ض) هم نهشت اند، نتیجه می گیریم پاره خط های PA و PB با هم برابر است.

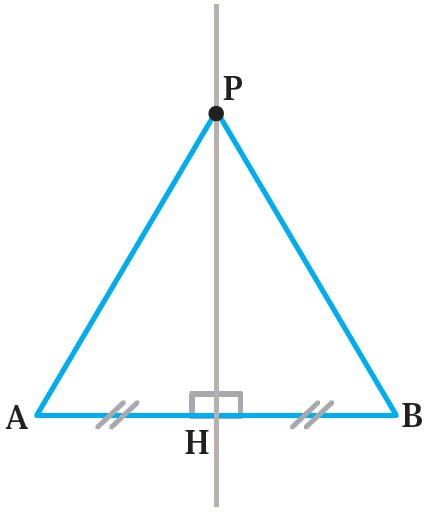
بنابراین فاصلهٔ نقطهٔ P، که روی عمودمنصف پاره خط AB است، از دو سر پاره خط AB یکسان اند.

آیا این اثبات برای اینکه نتیجه بگیریم نتیجهٔ بالا برای «هر» نقطهٔ روی عمودمنصف برقرار است، کافی است؟

چون نقطه P دلخواه می باشد با تغییر مکان نقطه P روی عمود منصف باز هم شرایط بر قرار است، بنابراین برای هر نقطه روی عمود منصف قابل تعمیم می باشد. (نقطه P نماینده تمام نقاط روی عمود منصف است)