جواب مثال صفحه 49 درس 3 ریاضی نهم (استدلال و اثبات در هندسه)
تعداد بازدید : 84.74Mپاسخ مثال صفحه 49 ریاضی نهم
-گام به گام مثال صفحه 49 درس استدلال و اثبات در هندسه
-مثال صفحه 49 درس 3
-شما در حال مشاهده جواب مثال صفحه 49 ریاضی نهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
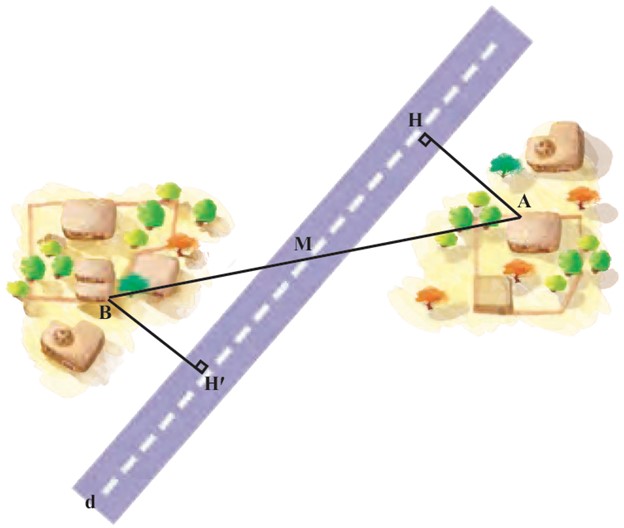
دو روستای A و B با یک جادّهٔ خاکی مستقیم به هم وصل هستند. در آن منطقه یک جادّهٔ آسفالتهٔ مستقیم ساخته شد که دو روستا در دو طرف آن واقع شد و جادهٔ آسفالته درست از وسط جادّهٔ خاکی عبور می کرد. ادارهٔ راه سازی تصمیم گرفته است که از هر روستا، یک جادّهٔ آسفالته با کوتاه ترین فاصلهٔ ممکن تا جادّهٔ اصلی بسازد. بنابراین از روستای A یک جادّهٔ مستقیم، عمود بر این جادّهٔ اصلی و به طول چهار کیلومتر ساخته شد. برای برآورد هزینه های ساخت جادّهٔ دیگر از روستای B، مهندسان پیش بینی کرده اند که فاصلهٔ روستای B از جاده نیز همین مقدار است؛ یعنی AH = BH’.
قدم های حل مسئله
1 صورت مسئله را به دقت بخوانید و مفاهیم تشکیل دهندهٔ آن را بشناسید. در این مسئله با مفاهیمی همچون خط، پاره خط و فاصلهٔ نقطه تا خط سرو کار داریم. آیا با آنها آشنایی دارید؟
خط:
مجموعهای از نقاط که از دو طرف تا بینهایت ادامه دارد.
در این مسئله: آن «جاده آسفالته مستقیم» که با نماد d نشان داده شده، یک خط است، چون سر و ته ندارد و از دو طرف ادامه دارد.
پاره خط:
قسمتی از یک خط که دو سرِ مشخص دارد.
در این مسئله: مسیر خاکی بین دو روستای A و B یک پارهخط است. همچنین وقتی M وسط آن قرار گرفته، MA و MB هم پارهخط هستند.
فاصله نقطه تا خط:
کوتاهترین مسیر از یک نقطه تا یک خط، که همیشه عمود بر آن خط است.
در این مسئله: وقتی میخواهیم از روستای A جادهای به جاده اصلی بسازیم، برای اینکه «کوتاهترین فاصله» باشد، باید آن را عمود رسم کنیم. به همین دلیل است که زاویه H قائمه 90 درجه) است. پس طول پارهخط AH، همان فاصله نقطه A تا خط d است.
2 اگر مسئله فاقد شکل است، با توجه به صورت مسئله، یک شکل مناسب برای آن رسم کنید. در اینجا شکل این مسئله را با توجه به طرح بالا رسم کنید.
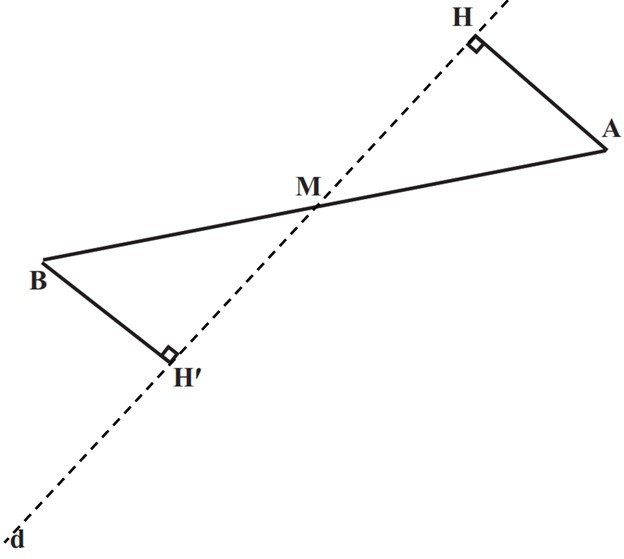
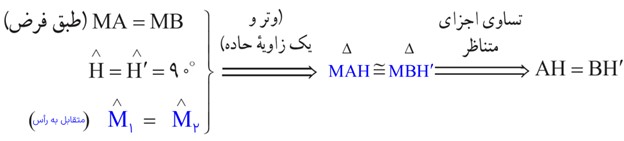
3 داده های مسئله (فرض) و خواسته های آن (حکم) را تشخیص دهید و در یک جدول بنویسید. دراینجا فرض های اصلی این است که M وسط AB است؛ یعنی MA = MB است و AH و BH’ بر d عمودند و حکم این است: AH = BH’
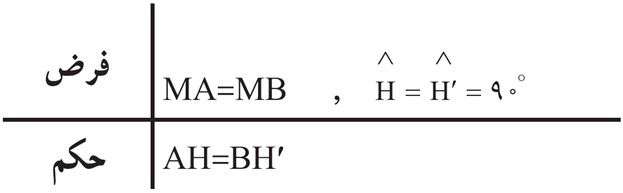
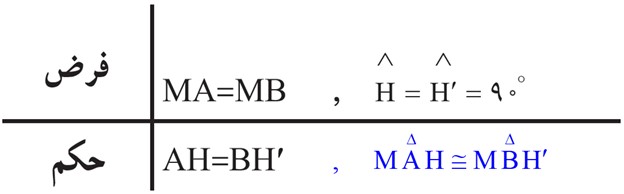
4 برای رسیدن از فرض به حکم، راه حلی پیدا کنید. روش های مختلفی برای این کار هست که آنها را به مرور می آموزید. یکی از راه های اثبات برابری دو پاره خط، استفاده از مثلث های هم نهشت است. در این شکل، کدام دو مثلث، برای این منظور مناسب است؟
با توجه به فرض و حکم مسئله، اثبات را با نمادهای ریاضی کامل کنید:

دو مثلث MAH و MBH:
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















