آیا تمام سوالات تمرین صفحه 42 ریاضی نهم، مطابق با آخرین تغییرات کتب درسی پاسخ داده شده است ؟

بله، تمام جواب ها به تمرین صفحه 42 ریاضی نهم مطابق با آخرین تغییرات کتب درسی 1402 - 1401 است.

آیا جواب ها به صورت آموزش محور و کامل بیان شده اند ؟

بله، جواب سوالات به صورت کاملا تشریحی و با هدف یادگیری و تسلط به مبحث بیان شده اند.

جواب تمرین صفحه 42 درس 3 ریاضی نهم (استدلال و اثبات در هندسه)

تعداد بازدید : 78.77M

پاسخ تمرین صفحه 42 ریاضی نهم

گام به گام تمرین صفحه 42 درس استدلال و اثبات در هندسه

تمرین صفحه 42 درس 3

شما در حال مشاهده جواب تمرین صفحه 42 ریاضی نهم هستید. ما در تیم مای درس، پاسخ‌نامه‌های کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کرده‌ایم. اگر به دنبال به‌روزترین پاسخ‌ها برای این صفحه هستید و می‌خواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخ‌های گام به گام، به گنجینه‌ای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مای‌درس را نصب نمایید.

1 آیا اثبات مسئله زیر معتبر است؟ برای پاسخ خود دلیل بیاورید.

مسئله: در هر مثلث، اندازهٔ زاویهٔ خارجی با مجموع اندازه های دو زاویهٔ داخلی غیرمجاور با آن برابر است.

اثبات: مثلث متساوی الاضلاع ABC را درنظر می گیریم. می دانیم که مجموع زوایای داخلی هر مثلث \({180^ \circ }\) است و زوایای \({\hat A_1}\) و \(\hat B\) و \(\hat C\) هر کدام \({60^ \circ }\) است؛ بنابراین

\(\begin{array}{l}{{\hat A}_1} + {{\hat A}_2} = {180^ \circ } \to {{\hat A}_2} = {180^ \circ } - {{\hat A}_1} = {180^ \circ } - {60^ \circ } = {120^ \circ }\\\\\hat B + \hat C = 60 + 60 = 120\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow {{\hat A}_2} = \hat B + \hat C\end{array}\)

برای اثبات یک مسئله باید آن را در یک شکل دلخواه انجام دهیم و اثبات در یک شکل خاص مورد قبول نمی باشد

\(\begin{array}{l}\hat A + \hat B + {{\hat C}_1} = {180^ \circ }\\\\{{\hat C}_2} + {{\hat C}_1} = {180^ \circ }\\\\ \Rightarrow \hat A + \hat B + {{\hat C}_1} = {{\hat C}_2} + {{\hat C}_1}\\\\ \Rightarrow \hat A + \hat B = {{\hat C}_2}\end{array}\)

در اثبات های هندسی نباید از شکل خاص کمک بگیریم

2 در سال گذشته با تعریف چند ضلعی های محدب آشنا شدید. تعریف چندضلعی محدب را می توان بدین صورت هم آورد: «یک چندضلعی محدب است؛ اگر هر پاره خطی که دو نقطهٔ دلخواِه درون آن چندضلعی را به هم وصل می کند، به طور کامل درون آن چند ضلعی قرار بگیرد.» هر ضلعی که محدب نباشد، مقعر است. آیا تشخیص های سه دانش آموز در مورد محدب و مقعر بودن چندضلعی های زیر و دلایلی که ارائه کرده اند، با توجه به تعریف بالا درست است؟ پاسخ خود را توضیح دهید.

نرگس: چند ضلعی مقابل محدب نیست؛ زیرا نقاط P و Q درون آن قرار دارد اما پاره خطی که آنها را به هم وصل می کند، به طور کامل در آن قرار نمی گیرد.

مهدیه: چندضلعی مقابل محدب است؛ زیرا نقاط T و S درون آن قرار دارد و پاره خطی که آنها را به هم وصل می کند، نیز به طور کامل در آن قرار دارد.

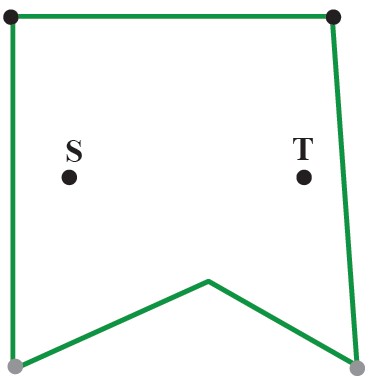
مریم: چندضلعی مقابل محدب است؛ زیرا نقاط M و N درون آن قرار دارد و پاره خطی که آنها را به هم وصل می کند، نیز به طور کامل در آن قرار دارد.

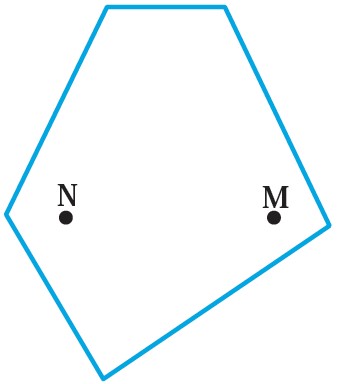
نرگس: برای اثبات محدب بودن باید وضعیت هر دو نقطه ی دلخواه را بررسی کنیم ولی یک مثال نقض برای محدب نبودن کافی است و در واقع نرگس پاره خط PQ را به عنوان مثال نقض برای محدب نبودن آورده است.

مهدیه: استدلال مهدیه نادرست است. زیرا این خاصیت باید برای هر دو نقطه ی دلخواه بررسی شود در این شکل می توان پاره خطی رسم کرد که نادرستی استدلال مهدیه را نشان دهد

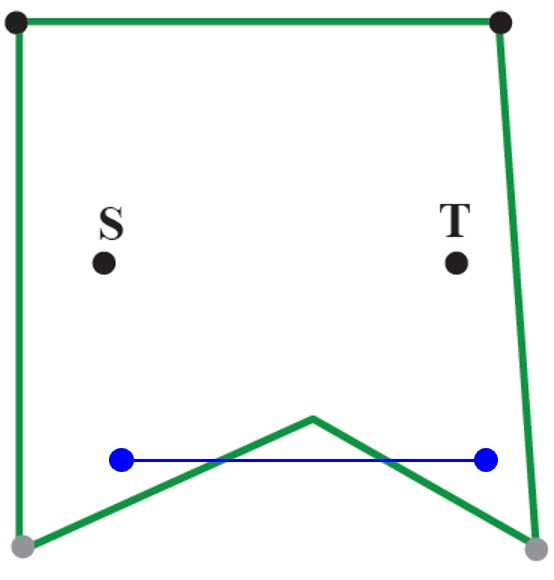
مریم: این 4 ضلعی محدب است ولی استدلال مریم ناقص است (درست نیست)

درواقع مریم باید برای هردو نقطه ی دلخواه این خاصیت را بررسی کند.

3 آیا استدلال های زیر درست است؟ پاسخ خود را توضیح دهید.

الف نادرست است. زیرا هر متوازی الاصلاع لزوماً یک مستطیل نیست در صورتی که هر مستطیل یک متوازی الاضلاع است

ب نادرست است. زیرا این 4 ضلعی می تواند لوزی باشد. لوزی چهار ضلعی است که چهار ضلع برابر دارد و می دانیم یک لوزی لزوماً یک مربع نیست در صورتی که تمام مربع ها لوزی می باشند

ج درست است. مربع یک چهار ضلعی است که چهار ضلع مساوی و چهار زاویه ی مساوی دارد چون چهار ضلع این چهارضلعی برابر نیست لذا می توان نتیجه گرفت ABCD مربع نمی باشد.

4 ثابت کنید هر نقطه که روی نیمساز زاویه قرار دارد، از دو ضلع آن زاویه به یک فاصله است.

یادآوری: فاصلهٔ یک نقطه از یک خط برابر است با طول پاره خطی که از آن نقطه بر خط عمود می شود.

راهنمایی: یک زاویهٔ دلخواه بکشید و نیمساز آن را رسم، و یک نقطه روی این نیمساز مشخص کنید. ثابت کنید فاصلهٔ این نقطه از دو ضلع زاویه با هم برابر است و سپس دلیل آن را که این نتیجه برای همهٔ نقاطِ روی نیمساز درست است، بیان کنید.

زاویه ی دلخواه xoy را در نظر می گیریم و نیم ساز آن را رسم می کنیم. نقطه ی C را به دلخواه روی آن در نظر می گیریم و از نقطه ی C دو عمود بر اضلاع oy , ox رسم می کنیم

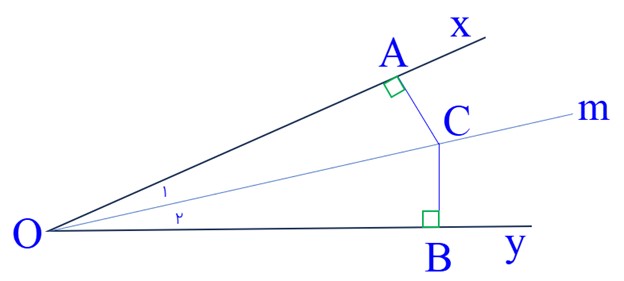
OA نیم ساز است؛ بنابراین:

\({\hat O_1} = {\hat O_2}\)

OC نیز وتر مشترک دو مثلث OAC و OBC هست.

همچنین زوایای A و B برابر با 90 درجه است. داریم:

\(\left\{ \begin{array}{l}{{\hat O}_1} = {{\hat O}_2}\\\\OC = OC\\\\\hat A = \hat B = {90^ \circ }\end{array} \right. \Rightarrow \) (بنابه حالت «و ز») \( \Rightarrow O\mathop A\limits^\Delta C \cong O\mathop B\limits^\Delta C\)

حال که هر دو مثلث هم نهشت هستند، اجزای متناظر آن ها هم با هم برابر است. بنابراین داریم:

AC = BC

چون نقطه ی C دلخواه است. بنابراین نتیجه می گیریم برای هر نقطه ی دلخواه روی نیم ساز این خاصیت برقرار است پس هر نقطه روی نیم ساز از دو ضلع آن زاویه به یک فاصله است.