جواب تمرین صفحه 69 درس 3 ریاضی یازدهم تجربی (تابع)
تعداد بازدید : 84.73Mپاسخ تمرین صفحه 69 ریاضی یازدهم تجربی
-گام به گام تمرین صفحه 69 درس تابع
-تمرین صفحه 69 درس 3
-شما در حال مشاهده جواب تمرین صفحه 69 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 با استفاده از نمودار تابع با ضابطهٔ f(x) = |x|، نمودار هر یک از توابع با ضابطه های زیر را رسم کنید.
الف \(g(x) = -|x|\)
ب \(h(x) = -|x - 3|\)
پ \(l(x) = 2|x – 2|\)
الف
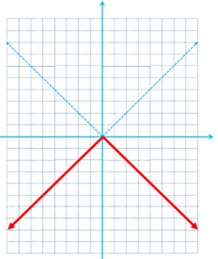
ب
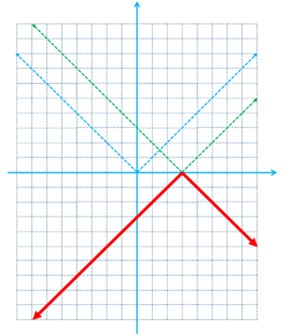
پ
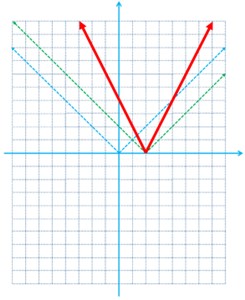
2 در هر مورد، دامنه و ضابطهٔ حاصل جمع، ضرب، تقسیم و تفریق دو تابع داده شده را بیابید.
الف \(f\left( x \right) = \left| x \right|\;\;\;\;g\left( x \right) = \frac{1}{x}\)
ب \(f\left( x \right) = {x^2} - 4\;\;\;\;\;\;g\left( x \right) = x + 2\)
پ \(f\left( x \right) = \sqrt x \;\;\;\;\;\;g\left( x \right) = - \sqrt x \)
ت \(f\left( x \right) = \frac{{x - 2}}{{x + 5}}\;\;\;\;\;\;\;g\left( x \right) = {x^2} + 3x - 10\)
ث \(f = \left\{ {\left( {2,5} \right)\;,\;\left( {3,4} \right)\;,\;\left( {0, - 2} \right)} \right\}\;\;\;\;\;g = \left\{ {\left( { - 1,2} \right)\;,\;\left( {0,3} \right)\;,\;\left( {2,4} \right)\;,\;\left( {3,0} \right)} \right\}\)
الف
\(\begin{array}{l}\left\{ \begin{array}{l}f\left( x \right) = \left| x \right|\quad ,\quad {D_f} = \mathbb{R}\\g\left( x \right) = \frac{1}{x}\quad ,\quad {D_g} = \mathbb{R} - \left\{ 0 \right\}\end{array} \right.\\\\\left( {f + g} \right)\left( x \right) = f\left( x \right) + g\left( x \right) = \left| x \right| + \frac{1}{x}\\\\ \Rightarrow {D_{f + g}} = {D_f} \cap {D_g} = \mathbb{R} - \left\{ 0 \right\}\\\\\left( {f - g} \right)\left( x \right) = f\left( x \right) - g\left( x \right) = \left| x \right| - \frac{1}{x}\\\\ \Rightarrow {D_{f - g}} = {D_f} \cap {D_g} = \mathbb{R} - \left\{ 0 \right\}\\\\\left( {f \cdot g} \right)\left( x \right) = f\left( x \right) \times g\left( x \right) = \left| x \right| \times \frac{1}{x} = \frac{{\left| x \right|}}{x}\\\\ \Rightarrow {D_{f \cdot g}} = {D_f} \cap {D_g} = \mathbb{R} - \left\{ 0 \right\}\\\\\left( {\frac{f}{g}} \right)\left( x \right) = \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{\left| x \right|}}{{\frac{1}{x}}} = x\left| x \right|\\\\ \Rightarrow {D_{\frac{f}{g}}} = {D_f} \cap {D_g} - \left\{ {\left. x \right|g\left( x \right) = 0} \right\} = \mathbb{R} - \left\{ 0 \right\} - \left\{ {} \right\} = \mathbb{R} - \left\{ 0 \right\}\end{array}\)
ب
\(\begin{array}{l}\left\{ \begin{array}{l}f\left( x \right) = {x^2} - 4\quad ,\quad {D_f} = \mathbb{R}\\g\left( x \right) = x + 2\quad ,\quad {D_g} = \mathbb{R}\end{array} \right.\\\\\left( {f + g} \right)\left( x \right) = f\left( x \right) + g\left( x \right) = {x^2} + x - 2\\\\ \Rightarrow {D_{f + g}} = {D_f} \cap {D_g} = \mathbb{R}\\\\\left( {f - g} \right)\left( x \right) = f\left( x \right) - g\left( x \right) = {x^2} - x - 6\\\\ \Rightarrow {D_{f - g}} = {D_f} \cap {D_g} = \mathbb{R}\\\\\left( {f \cdot g} \right)\left( x \right) = f\left( x \right) \times g\left( x \right)\\\\ = {x^3} + 2{x^2} - 4x - 8\\\\ \Rightarrow {D_{f \cdot g}} = {D_f} \cap {D_g} = \mathbb{R}\\\\\left( {\frac{f}{g}} \right)\left( x \right) = \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{{x^2} - 4}}{{x + 2}} = x - 2\\\\ \Rightarrow {D_{\frac{f}{g}}} = {D_f} \cap {D_g} - \left\{ {\left. x \right|g\left( x \right) = 0} \right\} = \mathbb{R} - \left\{ { - 2} \right\}\end{array}\)
پ
\(\begin{array}{l}\left\{ \begin{array}{l}f\left( x \right) = \sqrt x \quad ,\quad {D_f} = \left[ {0\;,\;\infty } \right)\\g\left( x \right) = - \sqrt x \quad ,\quad {D_g} = \left[ {0\;,\;\infty } \right)\end{array} \right.\\\\\left( {f + g} \right)\left( x \right) = f\left( x \right) + g\left( x \right) = \\\\\sqrt x - \sqrt x = 0 \Rightarrow {D_{f + g}} = {D_f} \cap {D_g} = \left[ {0\;,\;\infty } \right)\\\\\left( {f - g} \right)\left( x \right) = f\left( x \right) - g\left( x \right) = \\\\\sqrt x - \left( { - \sqrt x } \right) = 2\sqrt x \Rightarrow {D_{f - g}}\\\\ = {D_f} \cap {D_g} = \left[ {0\;,\;\infty } \right)\\\\\left( {f \cdot g} \right)\left( x \right) = f\left( x \right) \times g\left( x \right)\\\\ = \left( {\sqrt x } \right) \times \left( { - \sqrt x } \right) = - x\\\\ \Rightarrow {D_{f \cdot g}} = {D_f} \cap {D_g} = \left[ {0\;,\;\infty } \right)\\\\\left( {\frac{f}{g}} \right)\left( x \right) = \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{\sqrt x }}{{ - \sqrt x }} = - 1\\\\ \Rightarrow {D_{\frac{f}{g}}} = {D_f} \cap {D_g} - \left\{ {\left. x \right|g\left( x \right) = 0} \right\}\\\\ = \left[ {0\;,\;\infty } \right) - \left\{ 0 \right\} = \left( {0\;,\;\infty } \right)\end{array}\)
ت
\(\begin{array}{l}\left\{ \begin{array}{l}f\left( x \right) = \frac{{x - 2}}{{x + 5}}\quad ,\quad {D_f} = \mathbb{R} - \left\{ { - 5} \right\}\\g\left( x \right) = {x^2} + 3x - 10\quad ,\quad {D_g} = \mathbb{R}\end{array} \right.\\\\\left( {f + g} \right)\left( x \right) = f\left( x \right) + g\left( x \right)\\\\ = \frac{{x - 2}}{{x + 5}} + {x^2} + 3x - 10 \Rightarrow {D_{f + g}}\\\\ = {D_f} \cap {D_g} = \mathbb{R} - \left\{ { - 5} \right\}\\\\\left( {f - g} \right)\left( x \right) = f\left( x \right) - g\left( x \right)\\\\ = \frac{{x - 2}}{{x + 5}} - {x^2} - 3x + 10 \Rightarrow {D_{f - g}}\\\\ = {D_f} \cap {D_g} = \mathbb{R} - \left\{ { - 5} \right\}\\\\\left( {f \cdot g} \right)\left( x \right) = f\left( x \right) \times g\left( x \right) = \\\\\left( {\frac{{x - 2}}{{x + 5}}} \right) \times \left( {{x^2} + 3x - 10} \right)\\\\ = \left( {\frac{{x - 2}}{{x + 5}}} \right) \times \left( {x - 2} \right)\left( {x + 5} \right) = {\left( {x - 2} \right)^2}\\\\ \Rightarrow {D_{f \cdot g}} = {D_f} \cap {D_g} = \mathbb{R} - \left\{ { - 5} \right\}\\\\\left( {\frac{f}{g}} \right)\left( x \right) = \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{\frac{{x - 2}}{{x + 5}}}}{{{x^2} + 3x - 10}}\\\\ = \frac{{x - 2}}{{\left( {x + 5} \right)\left( {x - 2} \right)\left( {x + 5} \right)}} = \frac{1}{{{{\left( {x + 5} \right)}^2}}}\\\\ \Rightarrow {D_{\frac{f}{g}}} = {D_f} \cap {D_g} - \left\{ {\left. x \right|g\left( x \right) = 0} \right\}\\\\ = \mathbb{R} - \left\{ { - 5} \right\} - \left\{ { - 5\;,\;2} \right\} = \mathbb{R} - \left\{ { - 5\;,\;2} \right\}\end{array}\)
ث
\(\begin{array}{l}\left\{ \begin{array}{l}f = \left\{ {\left( {2\;,\;5} \right)\;,\;\left( {3\;,\;4} \right)\;,\;\left( {0\;,\; - 2} \right)} \right\}\quad ,\quad {D_f} = \left\{ {0\;,\;2\;,\;3} \right\}\\g = \left\{ {\left( { - 1\;,\;2} \right)\;,\;\left( {0\;,\;3} \right)\;,\;\left( {2\;,\;4} \right)\;,\;\left( {3\;,\;0} \right)} \right\}\quad ,\quad {D_g} = \left\{ { - 1\;,\;0\;,\;2\;,\;3} \right\}\end{array} \right.\\\\{D_{f + g}} = {D_f} \cap {D_g} = \left\{ {0\;,\;2\;,\;3} \right\}\\\\ \Rightarrow f + g = \left\{ {\left( {0\;,\; - 2 + 3} \right)\;,\;\left( {2\;,\;5 + 4} \right)\;,\;\left( {3\;,\;4 + 0} \right)} \right\}\\\\ = \left\{ {\left( {0\;,\;1} \right)\;,\;\left( {2\;,\;9} \right)\;,\;\left( {3\;,\;4} \right)} \right\}\\\\{D_{f - g}} = {D_f} \cap {D_g} = \left\{ {0\;,\;2\;,\;3} \right\} \Rightarrow f - g\\\\ = \left\{ {\left( {0\;,\; - 2 - 3} \right)\;,\;\left( {2\;,\;5 - 4} \right)\;,\;\left( {3\;,\;4 - 0} \right)} \right\}\\\\ = \left\{ {\left( {0\;,\; - 5} \right)\;,\;\left( {2\;,\;1} \right)\;,\;\left( {3\;,\;4} \right)} \right\}\\\\{D_{f \cdot g}} = {D_f} \cap {D_g} = \left\{ {0\;,\;2\;,\;3} \right\} \Rightarrow f \cdot g\\\\ = \left\{ {\left( {0\;,\; - 2 \times 3} \right)\;,\;\left( {2\;,\;5 \times 4} \right)\;,\;\left( {3\;,\;4 \times 0} \right)} \right\}\\\\ = \left\{ {\left( {0\;,\; - 6} \right)\;,\;\left( {2\;,\;20} \right)\;,\;\left( {3\;,\;0} \right)} \right\}\\\\{D_{\frac{f}{g}}} = {D_f} \cap {D_g} - \left\{ {\left. x \right|g\left( x \right) = 0} \right\} = \left\{ {0\;,\;2\;,\;3} \right\} - \left\{ 0 \right\}\\\\ = \left\{ {0\;,\;2} \right\} \Rightarrow \frac{f}{g} = \left\{ {\left( {0\;,\;\frac{{ - 2}}{3}} \right)\;,\;\left( {2\;,\;\frac{5}{4}} \right)} \right\}\end{array}\)
3 با استفاده از نمودار تابع با ضابطهٔ \(f\left( x \right) = \sqrt x \)، هر یک از نمودارهای زیر را رسم کنید.
الف \(r\left( x \right) = 2\sqrt x \)
ب \(s\left( x \right) = - \sqrt {x - 2} \)
پ \(t\left( x \right) = - 3\sqrt x \)
ت \(u\left( x \right) = 1 - \sqrt x \)
ث \(v\left( x \right) = 1 - \sqrt {x - 3} \)
الف
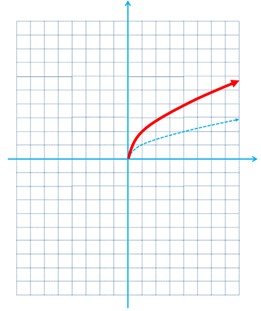
ب
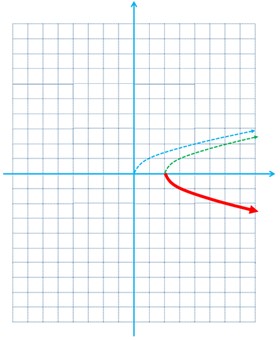
پ
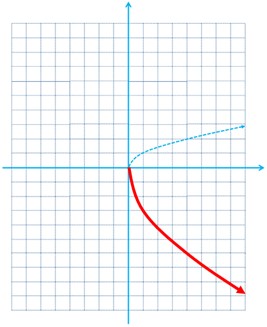
ت
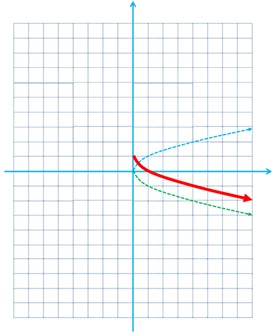
ث
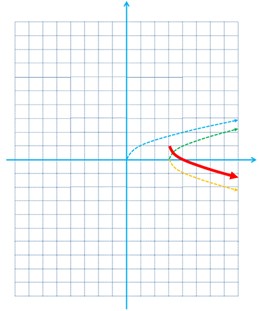
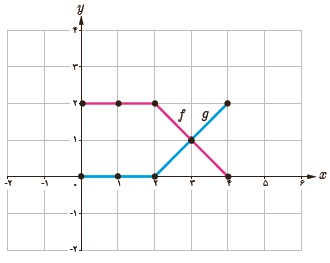
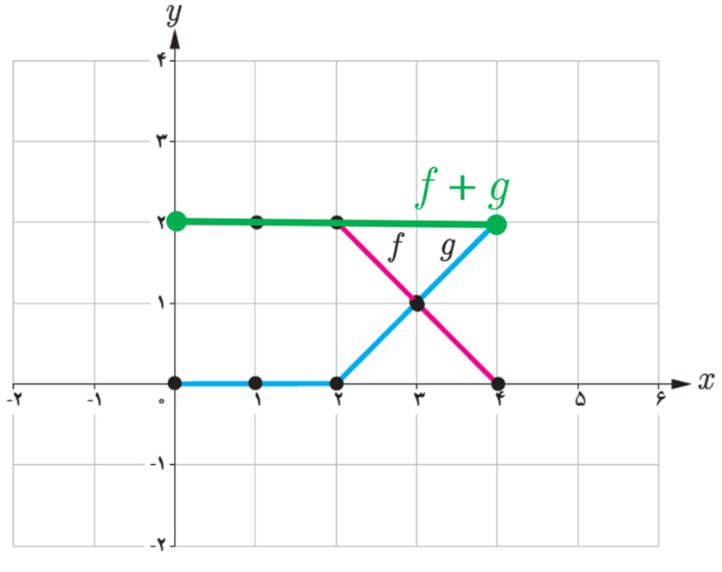
4 در شکل مقابل، نمودار دو تابع f و g رسم شده است. نمودار حاصل جمع این دو تابع را به دست آورید.
5 با توجه به نمودار سه تابع داده شده، مشخص کنید کدام یک از آنها برابر مجموع دو تابع دیگر است؟
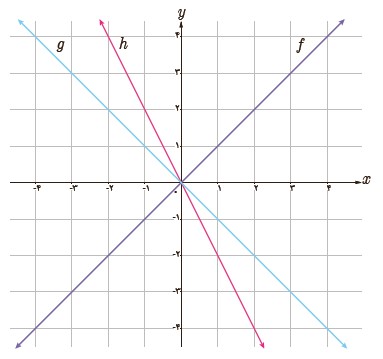
\(\left. \begin{array}{l}f\left( x \right) = x\\g\left( x \right) = - x\\h\left( x \right) = - 2x\end{array} \right\} \Rightarrow g\left( x \right) = f\left( x \right) + h\left( x \right) = x + \left( { - 2x} \right) = - x\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















