جواب فعالیت صفحه 53 درس 3 ریاضی یازدهم تجربی (تابع)

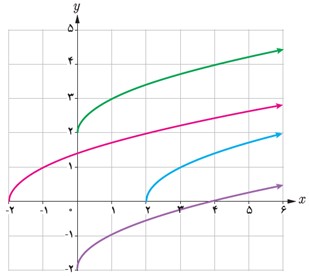
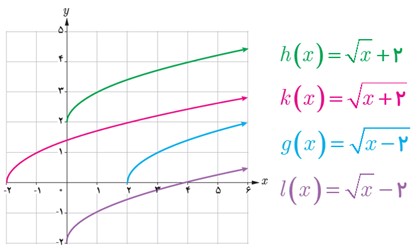
الف

\(g\left( x \right) = \sqrt {x - 2} \;\;\;{D_g} = \left[ {2\;,\; + \infty } \right)\)

ب

\(h\left( x \right) = \sqrt x + 2\;\;\;{D_h} = \left[ {0\;,\; + \infty } \right)\)

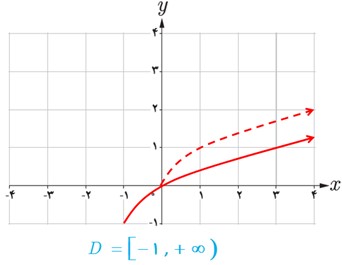
پ

\(k\left( x \right) = \sqrt {x + 2} \;\;\;{D_k} = \left[ { - 2\;,\; + \infty } \right)\)

ت

\(l\left( x \right) = \sqrt x - 2\;\;\;{D_l} = \left[ {0\;,\; + \infty } \right)\)

ابتدا در راستای طولی، تابع را جابجا می کنیم:

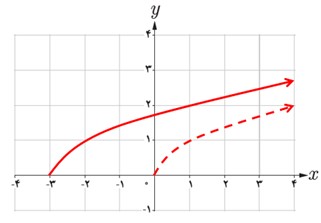
حال در راستای عرضی، تابع را جابجا می کنیم:

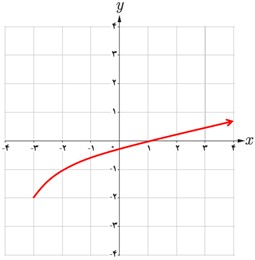
برای بدست آوردن دامنه تابع کافی است که عبارت داخل رادیکال را بزرگتر مساوی با صفر قرار دهیم و این نامعادله را حل کنیم. جواب های این نامعادله، دامنه تابع می باشند. برای تابع \(y = - 2 + \sqrt {x + 3} \) داریم:

\(\begin{array}{l}y = - 2 + \sqrt {x + 3} \\\\ \Rightarrow x + 3 \ge 0\\\\ \Rightarrow x \ge - 3\\\\ \Rightarrow D = [ - 3\,,\, + \infty )\end{array}\)

الف

\(\begin{array}{l}f\left( x \right) = \sqrt {3x - 6} \\\\f\left( 1 \right) = \sqrt {3(1) - 6} = \sqrt { - 3} \,\,\,x\\\\f\left( 2 \right) = \sqrt {3(2) - 6} = \sqrt 0 = 0\\\\f\left( 2 \right) = \sqrt {3(3) - 6} = \sqrt 3 \end{array}\)

ب

بله؛ زیرا جذر اعداد منفی تعریف نشده است.

پ

\(3x - 6 \ge 0 \Rightarrow 3x \ge 6 \Rightarrow x \ge 2\)

\([2\,,\, + \infty )\)

\(\begin{array}{l} - {x^2} + 1 \ge 0 \Rightarrow {x^2} \le 1 \Rightarrow - 1 \le x \le 1\\\\ \Rightarrow {D_f} = [ - 1\,,\,1]\end{array}\)

\(\begin{array}{l}{x^2} - 4 \ge 0 \Rightarrow {x^2} \ge 4 \Rightarrow \left\{ \begin{array}{l}x \le - 2\\\\x \ge 2\end{array} \right.\\\\ \Rightarrow {D_g} = ( - \infty \,,\, - 2] \cup [2\,,\, + \infty )\end{array}\)