1736019749.png)
جواب مثال صفحه 28 درس 1 آمار و احتمال یازدهم ریاضی (آشنایی با مبانی ریاضیات)
تعداد بازدید : 78.77Mپاسخ مثال صفحه 28 آمار و احتمال یازدهم ریاضی
-گام به گام مثال صفحه 28 درس آشنایی با مبانی ریاضیات
-مثال صفحه 28 درس 1
-شما در حال مشاهده جواب مثال صفحه 28 آمار و احتمال یازدهم ریاضی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
با استفاده از جبر مجموعه ها درستی هر یک از تساوی های زیر را بررسی کنید.
\(A - (B \cup C) = (A - B) \cap (A - C)\) الف
\(A \cap (B - C) = (A \cap B) - (A \cap C)\) ب
\(A - (B - C) = (A - B) - C\) پ
اگر \((A \cup B) = (A \cap B)\) آنگاه A=B ت
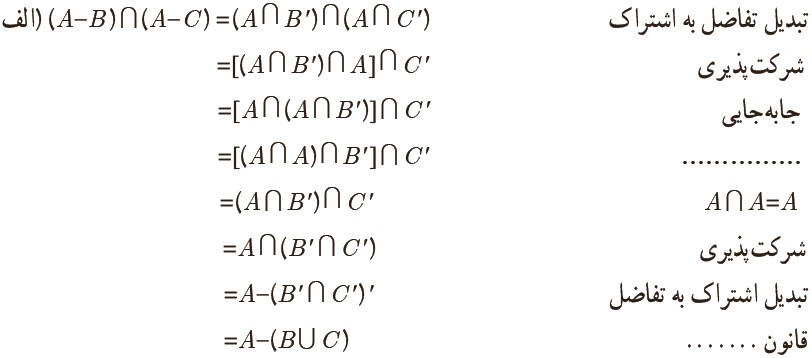
پ) با کمی تأمل پی می بریم که برای رسیدن از یک طرف تساوی به طرف دیگر، دچار مشکل می شویم و این کار انجام نمی شود، ولی برای اینکه ادعا کنیم این تساوی همواره برقرار نیست، کافی است مثال نقض بزنیم:
A={1 , 2 , 3 , 4 , 5} , B={3 , 4 , 5} , C={5 , 6 , 7} , U={1 , 2 , … , 10}
A-(B-C)={1 , 2 , 3 , 4 , 5} - {3 , 4} = {1 , 2 , 5}
(A-B)-C={1 , 2} - {5 , 6 , 7} = ………………
(A-B)-C={1 , 2} - {5 , 6 , 7} = {1 , 2}
ت) وقتی می نویسیم: C=D، یعنی C و D یک مجموعه اند، با دو نام و لذا وقتی بین مجموعه ها تساوی به کار می بریم، می توان نوشت طرفین تساوی را با هر مجموعه ای اجتماع، یا اشتراک بگیریم، یعنی از اینکه C=D نتیجه می شود: \(A \cup C = A \cup D\) و \(A \cap C = A \cap D\)
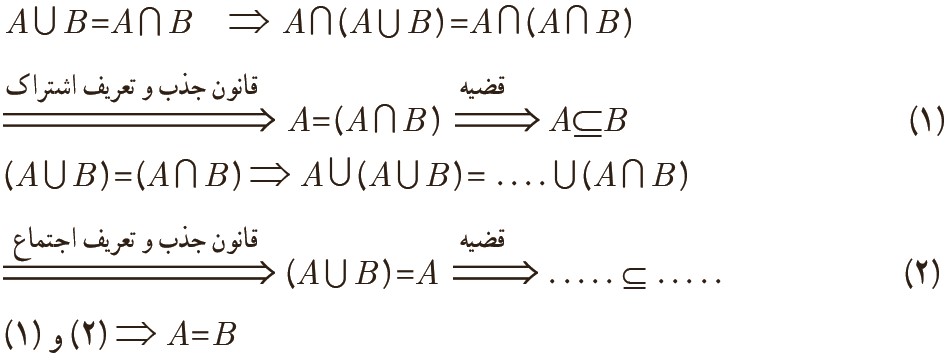
روش دوم: دربارهٔ روش زیر که به اختصار نوشته شده است، با هم کلاسی خود گفت و گو کنید و توضیح دهید:
\(A \subseteq (A \cup B) = (A \cap B) \subseteq B \Rightarrow A \subseteq B\)
فرض مسئله: \((A \cup B) = (A \cap B)\)
حکم مسئله: A=B
اثبات:
می دانیم که \(A \subseteq (A \cup B)\) همواره برقرار است و چون بنابر فرض مسئله که داریم \((A \cup B) = (A \cap B)\) ، نتیجه می شود که \(A \subseteq (A \cap B)\) و به این علت که رابطۀ \((A \cap B) \subseteq B\) همواره برقرار است داریم:
\(\left\{ \begin{array}{l}A \subseteq (A \cap B)\\\\(A \cap B) \subseteq B\end{array} \right. \Rightarrow A \subseteq B\)
و به طریق مشابه ثابت می شود: \(B \subseteq A\) و نتیجه می شود: A=B .
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
