جواب تمرین صفحه 14 درس 1 آمار و احتمال یازدهم ریاضی (آشنایی با مبانی ریاضیات)
تعداد بازدید : 84.72Mپاسخ تمرین صفحه 14 آمار و احتمال یازدهم ریاضی
-گام به گام تمرین صفحه 14 درس آشنایی با مبانی ریاضیات
-تمرین صفحه 14 درس 1
-شما در حال مشاهده جواب تمرین صفحه 14 آمار و احتمال یازدهم ریاضی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 در جاهای خالی عدد یا علامت مناسب قرار دهید، به طوری که گزاره های حاصل دارای ارزش درست باشند.
الف \({(0/1)^5}\,\,\, \ldots \,\,\,{(0/1)^3}\)
<
ب اگر \({0^ \circ } < \alpha < {45^ \circ }\) ، \(Sin\alpha \,\,\, \ldots \,\,\,Cos\alpha \)
<
پ نمودار تابع \(y = {x^2}\) از نقطه ... می گذرد.
(0 , 0)
ت \( - {(x - 4)^2}\,\,\, \ldots \,\,\,0\)
\( \le \)
ث \({y^2} = {x^2}\) تابع ...
نیست
ج اگر \({x^2} = a\) آن گاه \(x = \,\,\, \ldots \)
\( \pm \sqrt a \)
2 نقیض گزاره های زیر را بنویسید.
الف اگر \(0 < x < 1\) ، آن گاه \({x^2} < x\)
نقیض گزاره \(p \Rightarrow q\) هم ارز با \(p \wedge \sim q\) است؛ به عبارتی:
\( \sim (p \Rightarrow q) \equiv p \wedge \sim q\)
بنابراین نقیض گزاره الف به صورت زیر می شود:
\({x^2} \ge x\) و \(0 < x < 1\)
داریم:
\(\begin{array}{l}p:\,\,0 < x < 1 \Rightarrow x \in (0\,,\,1)\\\\ \sim q:\,{x^2} \ge x \Rightarrow x \in \mathbb{R} - (0\,,\,1)\\\\ \Rightarrow p \wedge \sim q = \left\{ {x \in (0\,,\,1)} \right\} \wedge \left\{ {x \in \mathbb{R} - (0\,,\,1)} \right\} = (0\,,\,1) \cap \mathbb{R} - (0\,,\,1) = \emptyset \end{array}\)
در نهایت نقیض گزاره مسئله برابر تهی می شود.
ب ابوالوفا محمد بوزجانی، ریاضی دان است.
ابوالوفا محمد بوزجانی، ریاضی دان نیست.
پ \(a \in \{ b\,,\,c\,,\,d\} \)
\(a \notin \{ b\,,\,c\,,\,d\} \)
ت 2 عددی زوج است یا عدد \(\pi \) گویاست.
2 عددی فرد است و عدد \(\pi \) غیر گویاست.
3 ارزش گزاره های مرکب زیر را تعیین کنید.
الف \((2 < 3) \wedge (4 + 3 = 10)\)
\(\left. \begin{array}{l}(2 < 3) \equiv T\\\\(4 + 3 = 10) \equiv F\end{array} \right\} \Rightarrow (2 < 3) \wedge (4 + 3 = 10) \equiv F\)
بنابراین ارزش گزاره، نادرست است.
ب \((5 > 3) \vee ({( - 1)^2} + 1 = 0)\)
\(\left. \begin{array}{l}(5 > 3) \equiv T\\\\({( - 1)^2} + 1 = 0) \equiv F\end{array} \right\} \Rightarrow (5 > 3) \vee ({( - 1)^2} + 1 = 0) \equiv T\)
بنابراین ارزش گزاره، درست است.
پ \((\frac{1}{2} \ne \frac{3}{6}) \vee (1 \in \{ 2\,,\,3\,,\,4\} )\)
\(\left. \begin{array}{l}(\frac{1}{2} \ne \frac{3}{6}) \equiv F\\\\(1 \in \{ 2\,,\,3\,,\,4\} ) \equiv F\end{array} \right\} \Rightarrow (\frac{1}{2} \ne \frac{3}{6}) \vee (1 \in \{ 2\,,\,3\,,\,4\} ) \equiv F\)
بنابراین ارزش گزاره، نادرست است.
ت اگر عدد 4 فرد باشد، آن گاه 4 مربع کامل نیست.
گزاره «عدد 4 فرد باشد» نادرست است
گزاره «4 مربع کامل نیست» نادرست است
بنابراین:
\(\left. \begin{array}{l}p \equiv F\\\\q \equiv F\end{array} \right\} \Rightarrow (p \Rightarrow q) \equiv T\)
در نتیجه گزاره ت درست است.
ث 2 عدد اوّل نیست، اگر و تنها اگر 2 مربع کامل است.
گزاره «2 عدد اول نیست» نادرست است
گزاره «2 مربع کامل است» نادرست است
بنابراین:
\(\left. \begin{array}{l}p \equiv F\\\\q \equiv F\end{array} \right\} \Rightarrow (p \Leftrightarrow q) \equiv T\)
در نتیجه گزاره ث درست است.
ج \(2 > 3 \Leftrightarrow - 2 < - 3\)
\(\left. \begin{array}{l}2 > 3 \equiv F\\\\ - 2 < - 3 \equiv F\end{array} \right\} \Rightarrow (2 > 3 \Leftrightarrow - 2 < - 3) \equiv T\)
بنابراین ارزش گزاره، درست است.
چ اگر \(a \in \{ b\} \) آن گاه a=b و برعکس.
گزاره را با نمادهای ریاضی می نویسیم:
\(a \in \{ b\} \Leftrightarrow a = b\)
گزاره اول با گزاره دوم مرتبط می باشد؛ پس در دو حالت بایستی ارزش گزاره کلی را بررسی نماییم:
حالت اول:
کزاره اول و دوم هر دو درست می باشند:
\(\left. \begin{array}{l}a \in \{ b\} \equiv T\\\\a = b \equiv T\end{array} \right\} \Rightarrow (a \in \{ b\} \Leftrightarrow a = b) \equiv T\)
در صورت درست بودن دو گزاره اول و دوم،گزاره کلی درست می باشد.
حالت دوم:
کزاره اول و دوم هر دو نادرست می باشند:
\(\left. \begin{array}{l}a \in \{ b\} \equiv F\\\\a = b \equiv F\end{array} \right\} \Rightarrow (a \in \{ b\} \Leftrightarrow a = b) \equiv F\)
در صورت نادرست بودن دو گزاره اول و دوم،گزاره کلی درست می باشد.
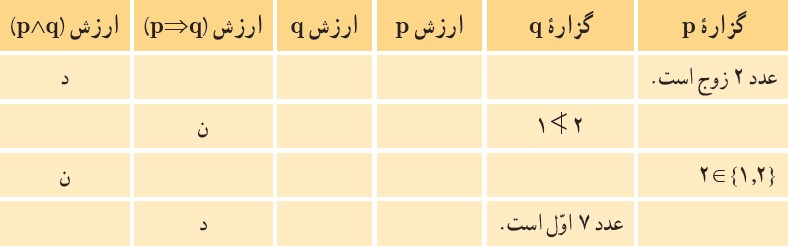
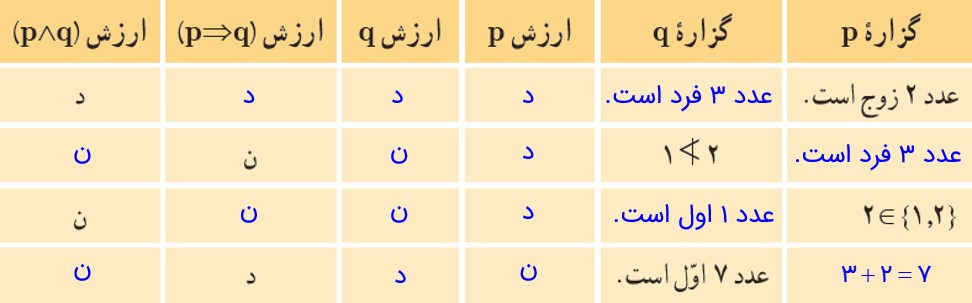
4 جدول زیر را کامل کنید.
5 جدول ارزش های هر یک از گزاره های زیر را رسم کنید.
الف \(p \wedge \sim q\)
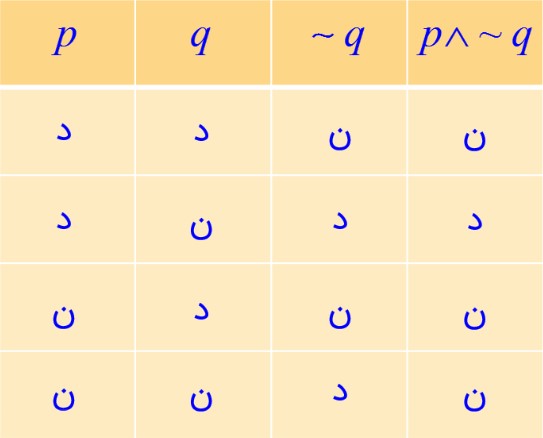
ب \( \sim p \wedge p\)
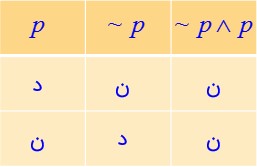
پ \( \sim p \vee p\)

ت \((p \vee q) \wedge \sim p\)
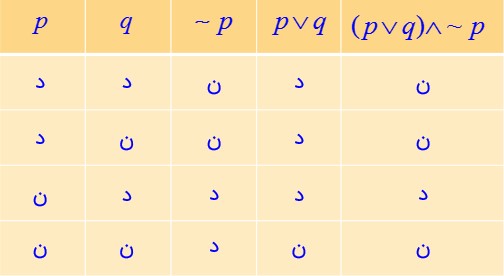
ث \((p \vee q) \Leftrightarrow q\)
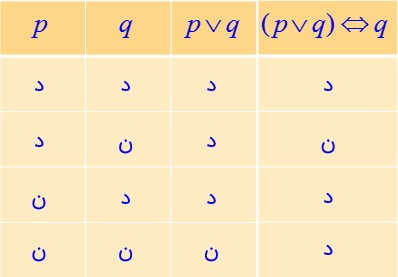
ج \( \sim p \Leftrightarrow \sim q\)
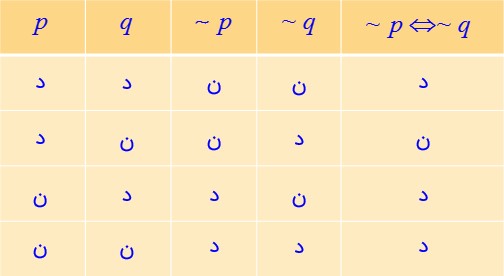
6 با استفاده از جدول ارزش ها نشان دهید که:
الف \(p \Rightarrow p \equiv T\)
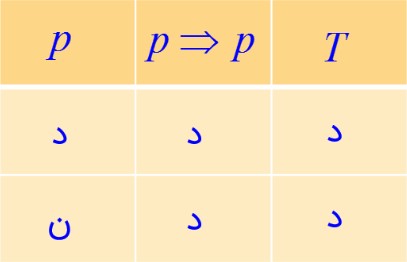
بنابراین \(p \Rightarrow p \equiv T\) می باشد.
ب \(p \vee F \equiv p\)

بنابراین \(p \vee F \equiv p\) می باشد.
پ \(p \wedge T \equiv p\)
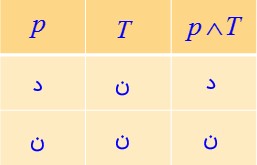
بنابراین \(p \wedge T \equiv p\) می باشد.
ت \( \sim (p \Rightarrow q) \equiv p \wedge \sim q\)

بنابراین \( \sim (p \Rightarrow q) \equiv p \wedge \sim q\) می باشد.
ث \(p \wedge (q \vee p) \equiv p\)
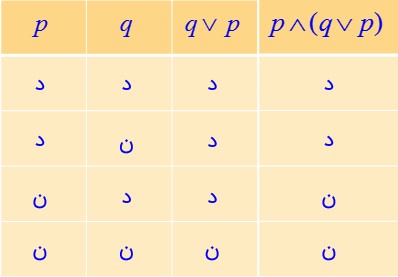
بنابراین \(p \wedge (q \vee p) \equiv p\) می باشد.
ج \(p \vee (q \wedge p) \equiv p\)
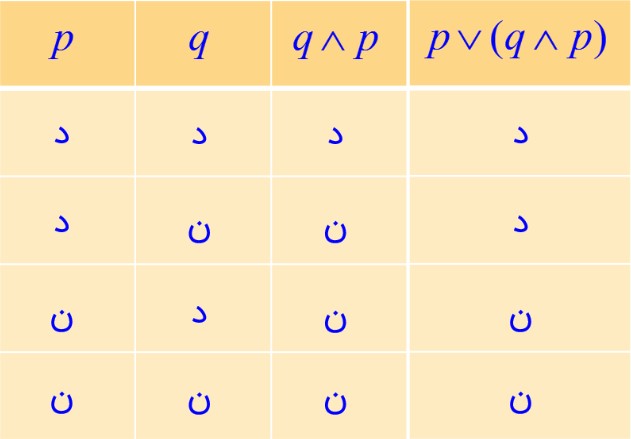
بنابراین \(p \vee (q \wedge p) \equiv p\) می باشد.
چ \(p \Rightarrow (q \Rightarrow r) \equiv (p \wedge q) \Rightarrow r\)
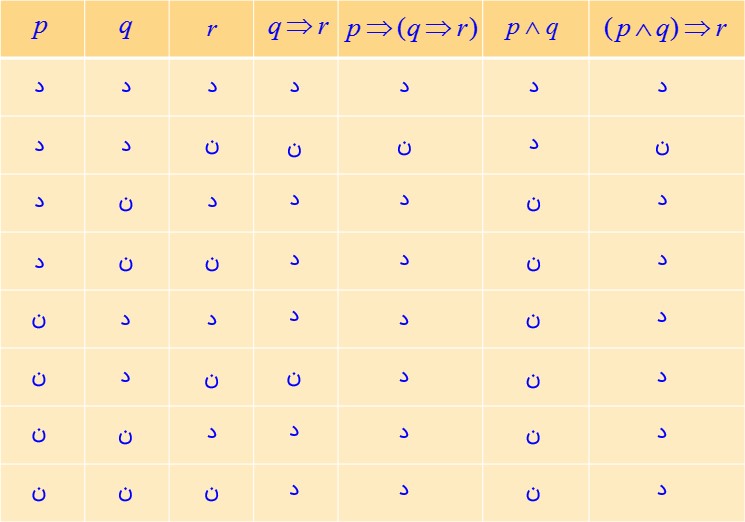
بنابراین \(p \Rightarrow (q \Rightarrow r) \equiv (p \wedge q) \Rightarrow r\) می باشد.
ح \( \sim (p \Leftrightarrow q) \equiv \sim p \Leftrightarrow q\)

بنابراین \( \sim (p \Leftrightarrow q) \equiv \sim p \Leftrightarrow q\) می باشد.
7 ثابت کنید هرگاه n عددی صحیح و \({n^2}\) مضرب 3 باشد، آن گاه n نیز مضرب 3 است.
به جای اثبات این حکم، عکس نقیض آن را ثابت می کنیم. یعنی نشان می دهیم.
چنانچه n مضرب 3 نباشد، یعنی باقیمانده تقسیم آن بر 3 برابر 1 یا 2 است. به عبارت دیگر:
\(\begin{array}{l}n = 3k + 1 \Rightarrow {n^2} = 9{k^2} + 6k + 1 = 3(3{k^2} + 2k) + 1\\\\ \Rightarrow {n^2} = 3k' + 1\end{array}\)
در این حالت \({n^2}\) مضرب 3 نیست.
\(\begin{array}{l}n = 3k + 2 \Rightarrow {n^2} = 9{k^2} + 12k + 4 = 3(3{k^2} + 4k + 1) + 1\\\\ \Rightarrow {n^2} = 3k'' + 1\end{array}\)
در این حالت نیز \({n^2}\) مضرب 3 نیست.
در نتیجه حکم سوال برقرار است.
8 گزاره های زیر را با استفاده از نمادهای \(\exists \,,\,\forall \) بنویسید و ارزش هر یک را با ذکر دلیل مشخص کنید.
الف هر عدد طبیعی زوج یا فرد است.
\(\forall a \in \mathbb{N}\,;\,(a \in E \vee a \in O)\)
درست است:
زیرا اگر عدد زوج باشد، فرد نخواهد بود و اگر عددی زوج نباشد فرد خواهد بود. در نتیجه در ترکیب فصلی یکی از گزاره ها درست و یکی نادرست است، پس در کل درست است.
ب برای بعضی از مقادیر a در مجموعه اعداد حسابی داریم: \({a^2} < 0\).
\(\exists a \in W\,;\,{a^2} < 0\)
نادرست است:
زیرا عددی وجود ندارد که مربع آن منفی شود به عبارت دیگر مجموعه جواب آن تهی است.
پ همهٔ اعداد اوّل فرد اند.
\(\forall a \in P\,;\,a \in O\)
زیرا به عنوان مثال نقض، عدد 2 اول بوده ولی فرد نیست.
ت عدد صحیح مثبتی وجود دارد مانند x به طوری که 1-2x>5
\(\exists x \in \mathbb{Z}\,;\,1 - 2x > 5\)
نادرست است:
زیرا \(1 - 2x > 5 \Rightarrow x < - 2\) ، یعنی x منفی است و هیچ عدد مثبتی در آن صدق نمی کند.
ث حاصل جمع هر عدد حقیقی ناصفر با معکوسش، بزرگ تر یا مساوی 2 است.
\(\forall a \in R - \{ 0\} \,;\,x + \frac{1}{x} \ge 2\)
نادرست است:
به عنوان نمونه x=-1 مثال نقض است زیرا \( - 1 + \frac{1}{{ - 1}} = - 2 < 2\)
ج به ازای بعضی از مقادیر حقیقی داریم \({x^3} = x\).
\(\exists x \in R\,;\,{x^3} = x\)
درست است:
زیرا مجموعه جواب آن \(S = \{ - 1\,,\,0\,,\,1\} \) ناتهی است.
9 هرگاه \(A = \{ x \in \mathbb{Z}|0 < x \le 5\} \) دامنهٔ متغیر باشد، ارزش گزاره های سوری زیر را تعیین کنید.
الف \(\exists x \in A;x + 4 = 10\)
نادرست است:
\(x + 4 = 10 \Rightarrow x = 6 \Rightarrow S = \{ \} \)
یعنی جوابی برای این گزاره وجود ندارد.
ب \(\forall x \in A;x + 2 \le 9\)
نادرست است:
زیرا \(x + 2 \le 9 \Rightarrow x \le 7 \Rightarrow S = \{ 1\,,\,2\,,\,3\,,\,4\,,\,5\} = A\) یعنی تمام اعضای دامنه تغییر جواب هستند.
پ \(\exists x \in A;x + 3 \le 4\)
درست است:
\(x + 3 \le 4 \Rightarrow x \le 1 \Rightarrow S = \{ 1\} \)
ت \(\forall x \in A;x + 1 \ge 6\)
درست است:
\(x + 1 \ge 6 \Rightarrow x \le 5 \Rightarrow S = \{ 5\} \)
فقط برای یک عضو دامنه تغییر برقرار است و اعدادی مثل 1، 2، 3 و 4 مثال نقض برای آن می باشند.
10 ارزش گزاره های سوری زیر را تعیین کنید، سپس نقیض هر یک را بنویسید.
الف \(\forall x \in \mathbb{R};\frac{{{x^2} - 1}}{{x - 1}} = x + 1\)
نادرست است:
زیرا برای x=1 تساوری داده شده، تعریف نمی شود. نقیض گزاره:
\(\exists x \in \mathbb{R};\frac{{{x^2} - 1}}{{x - 1}} \ne x + 1\)
ب \(\forall n \in \mathbb{N};({2^n} + 1) \in P\)
نادرست است:
در حالت n=5 عدد به دست آمده اول نیست؛ زیرا بر 641 بخش پذیر است. نقیض گزاره:
\(\exists n \in \mathbb{N};{2^{2n}} \notin P\)
پ \(\forall x \in ( - \infty \,,\,0);x - \frac{1}{x} \le - 2\)
نادرست است:
به عنوان نمونه x=-1 مثال نقض است؛ زیرا \( - 1 - \frac{1}{{ - 1}} = 0 > - 2\). نقیض گزاره:
\(\exists n \in ( - \infty \,,\,0);x - \frac{1}{x} > - 2\)
ت \(\exists y \in \mathbb{R};\frac{{y - 3}}{5} = 0\)
درست است:
زیرا مجموعه جواب آن S={3} ناتهی است. نقیض گزاره:
\(\forall y \in \mathbb{R};\frac{{y - 3}}{5} \ne 0\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















