شاه کلید نکات
شاه کلید سوال
1 دور زمین هایی مطابق شکل حصارکشی شده است. چطور می توان بدون کم و زیاد کردن حصارها، مساحت زمین را افزایش داد؟
الف
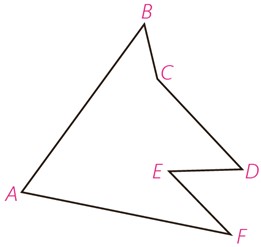
ب
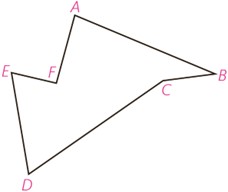
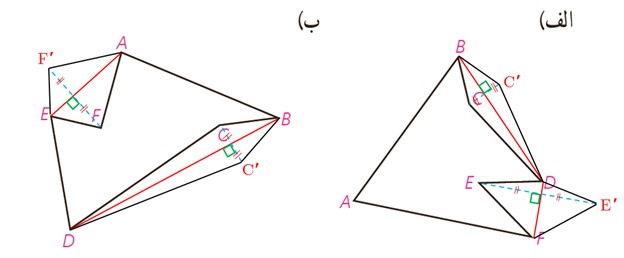
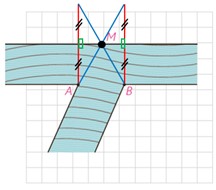
2 می خواهیم کنار رودخانه ها، 3 اسکله بسازیم. جای 2 اسکله A و B مطابق شکل مشخص است. اسکله M را در چه نقطه ای از ساحل رودخانه بسازیم که قایق ها هنگام طی مسیر MABM کوتاه ترین مسیر را طی کنند؟
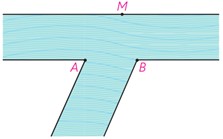
با توجه به شکل، واضح است که عرض رودخانه در طول مسیر ثابت در نظر گرفته شده است. پس یا از نقطه A یا از B روش هرون را برای پیدا کردن نقطه M اجرا می کنیم.
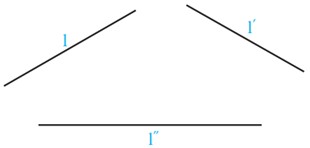
3 سه خط دو به دو ناموازی l و ʹl و ʺl در صفحه مفروض اند. پاره خطی به طول 5 سانتی متر رسم کنید که دو سر آن روی l و ʹl ، و موازی ʺl باشد.
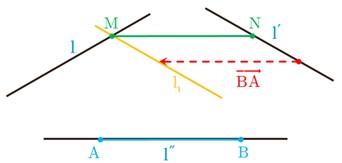
ابتدا روی خط l’’ پاره خط AB به طول 5 سانتی متر را مشخص می کنیم. خط l’ را تحت بردار BA انتقال می دهیم تا خط l1 بدست آید. این خط، l را در نقطه ای مانند M قطع می کند. از نقطه M موازی خط l’’ ، خطی رسم می کنیم تا خط l’ را در نقطه N قطع کند. پاره خط MN جواب مسئله است.
4 فرض کنید G محل برخورد میانه های مثلث ABC (مرکز ثقل آن) باشد و مثلث ʹAʹ BʹC مجانس مثلث ABC در تجانس به مرکز G و نسبت \(K = - \frac{1}{2}\) باشد.
الف جایگاه رأس های ʹA و ʹB و ʹC نسبت به مثلث ABC کجاست؟
ب مساحت مثلث ʹAʹ BʹC چه کسری از مساحت مثلث ABC است؟
الف
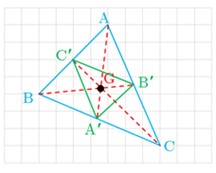
A’ وسط BC و B’ وسط AC و C’ وسط AB قرار دارند. با توجه به خاصیت مرکز ثقل می دانیم که \(GA' = \frac{1}{2}GA\). همچنین نقطه G بین A و A’ ، پس نقطه A’ مجانس نقطه A به مرکز تجانس G و نسبت تجانس \(\frac{1}{2}\) است. همین مطلب در مورد B’ و C’ نیز صدق می کند.
ب
با توجه به خاصیت تجانس، مساحت مثلث A’B’C’ برابر \(\frac{1}{4}\) مساحت مثلث ABC است.
5 زمینی به شکل زیر داریم، می خواهیم بدون آنکه محیط این زمین تغییر کند مساحتش را افزایش دهیم در هر مورد میزان افزایش مساحت را حساب کنید.
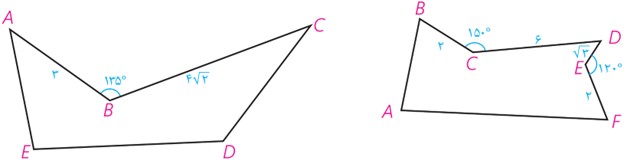
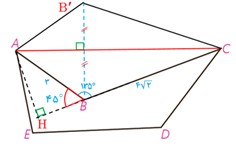
\(\begin{array}{l}AH = AB\,.\,\sin 45^\circ \\\\{S_{A\mathop B\limits^\Delta C}} = \frac{1}{2}AH\,.\,BC = \frac{1}{2} \times 3 \times \frac{{\sqrt 2 }}{2} \times 4\sqrt 2 = 6\\\\S = 2 \times {S_{A\mathop B\limits^\Delta C}} = 12\end{array}\)
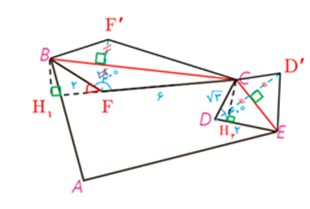
\(\begin{array}{l}B{H_1} = BF\,.\,\sin 30^\circ \\\\{S_{B\mathop F\limits^\Delta C}} = \frac{1}{2}\,B{H_1}\,.\,FC = \frac{1}{2} \times 2 \times \frac{1}{2} \times 6 = 3\\\\C{H_2} = CD\,.\,\sin 60^\circ \\\\{S_{C\mathop D\limits^\Delta E}} = \frac{1}{2}C{H_2}\,.\,DE = \frac{1}{2} \times \sqrt 3 \times \frac{{\sqrt 3 }}{2} \times 2 = \frac{3}{2}\\\\S = 2\,({S_{B\mathop F\limits^\Delta C}} + {S_{C\mathop D\limits^\Delta E}}) = 2\,(3 + \frac{3}{2}) = 9\end{array}\)
1736019749.png)
