شاه کلید نکات
شاه کلید سوال
مثلث متساوی الاضلاعی را در نظر بگیرید:
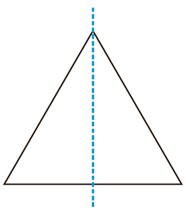
الف بازتاب این مثلث نسبت به خط داده شده چگونه است؟................
ب آیا تحت این بازتاب تصویر هر نقطه از شکل لزوماً خود آن نقطه است؟.........
پ آیا تحت این بازتاب، تصویر هر نقطه از شکل، روی خود شکل است؟
ت آیا خط بازتاب دیگری برای این مثلث سراغ دارید؟ ..........
این مثلث چند خط بازتاب دارد؟ ........
ث آیا غیر از بازتاب، تبدیل دیگری سراغ دارید که هر نقطه از شکل را به نقطه ای از همان شکل ببرد؟ ............
برای مثال آیا با مرکز O (نقطه همرسی نیمسازها) می توانید دوران هایی معرفی کنید که شکل را بر خودش منطبق کند؟ .........
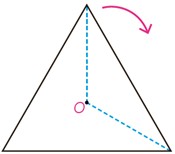
اگر \(0 < \alpha \le 360\) زاویه دوران باشد، چند دوران به مرکز O و زاویه α می توانید مشخص کنید؟ ...........
اگر \(0<α< 360\) زاویه دوران باشد، چند دوران به مرکز O و زاویه α می توانید مشخص کنید؟ ...........
الف
بازتاب این مثلث نسبت به خط داده شده، دقیقاً خود مثلث است.
خطی که در تصویر نشان داده شده، محور تقارن مثلث متساویالاضلاع است. محور تقارن مانند یک آینه عمل میکند. وقتی شکلی را نسبت به محور تقارنش بازتاب میدهیم، هر نقطه از یک طرف خط، دقیقاً روی نقطهی متناظرش در طرف دیگر قرار میگیرد. چون مثلث متساویالاضلاع از دو طرف این خط کاملاً یکسان است، بازتاب آن هیچ تغییری در شکل کلی ایجاد نمیکند و مثلث کاملاً بر روی خودش منطبق میشود.
ب
خیر.
نقاط روی خط بازتاب:
تنها نقاطی که دقیقاً روی خط بازتاب قرار دارند، پس از بازتاب روی خودشان باقی میمانند.
نقاط دیگر:
هر نقطهای که روی خط بازتاب نباشد، به نقطهی دیگری در سمت مقابل خط منتقل میشود. این نقطه جدید همان فاصلهای را از خط تقارن دارد که نقطه اصلی داشت.
پ
بله.
درست است که تصویر یک نقطه لزوماً خود آن نقطه نیست، اما به دلیل تقارن کامل شکل، تصویر آن حتماً نقطهای درون مرزهای همان مثلث خواهد بود. به عبارت دیگر، بازتاب، هیچ نقطهای را به خارج از مثلث منتقل نمیکند، بلکه صرفاً نقاط را درون خود مثلث جابجا میکند.
ت
بله، دو خط بازتاب دیگر نیز وجود دارد. مثلث متساویالاضلاع در مجموع سه خط بازتاب (محور تقارن) دارد.
هر محور تقارن در مثلث متساویالاضلاع، خطی است که از یک رأس به وسط ضلع مقابل آن رسم میشود. چون این مثلث سه رأس و سه ضلع برابر دارد، پس سه محور تقارن نیز خواهد داشت.
ث
بله، دوران. میتوان دورانهایی به مرکز O (محل همرسی نیمسازها) تعریف کرد که شکل را بر خودش منطبق کند.
نقطهی O مرکز تقارن دورانی مثلث است. اگر مثلث را حول این نقطه بچرخانیم:
دوران ۱۲۰ درجه:
رأس بالایی به جای رأس سمت راست پایین قرار میگیرد و کل مثلث دقیقاً جای خودش را پر میکند.
دوران ۲۴۰ درجه:
رأس بالایی به جای رأس سمت چپ پایین قرار میگیرد و مثلث دوباره بر خودش منطبق میشود.
(دوران ۳۶۰ درجه):
مثلث یک دور کامل میزند و به حالت اولیه خود بازمیگردد.
بنابراین، برای زاویههایی بین ۰ و ۳۶۰ درجه، دو دوران (۱۲۰ و ۲۴۰ درجه) وجود دارد که مثلث متساویالاضلاع را بر خودش منطبق میکند.
1736019749.png)
