آیا تمام سوالات سؤال متن صفحه 52 هندسه یازدهم، مطابق با آخرین تغییرات کتب درسی پاسخ داده شده است ؟

بله، تمام جواب ها به سؤال متن صفحه 52 هندسه یازدهم مطابق با آخرین تغییرات کتب درسی 1402 - 1401 است.

آیا جواب ها به صورت آموزش محور و کامل بیان شده اند ؟

بله، جواب سوالات به صورت کاملا تشریحی و با هدف یادگیری و تسلط به مبحث بیان شده اند.

جواب سؤال متن صفحه 52 درس 2 هندسه یازدهم (تبدیل های هندسی و کاربردها)

تعداد بازدید : 78.77M

پاسخ سؤال متن صفحه 52 هندسه یازدهم

گام به گام سؤال متن صفحه 52 درس تبدیل های هندسی و کاربردها

سؤال متن صفحه 52 درس 2

شما در حال مشاهده جواب سؤال متن صفحه 52 هندسه یازدهم هستید. ما در تیم مای درس، پاسخ‌نامه‌های کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کرده‌ایم. اگر به دنبال به‌روزترین پاسخ‌ها برای این صفحه هستید و می‌خواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخ‌های گام به گام، به گنجینه‌ای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مای‌درس را نصب نمایید.

مسائل پیدا کردن کوتاهترین مسیر:

الف) هرون، ریاضی دانی است که به او دایرةالمعارف ریاضی و فیزیک لقب داده اند. او که در فاصلهٔ زمانی 250 تا 150 سال قبل از میلاد مسیح در مصر زندگی می کرد برای نخستین بار به کمک بازتاب، دستور پیدا کردن کوتاه ترین مسیر را در شرایطی خاص ارائه کرد.

او با این مسئله روبه رو شده بود که:

«مردی می خواهد برای برداشتن آب از خانه به ساحل رودخانه ای که لبهٔ مستقیمی دارد برود و بعد سطل آب را به اسطبل ببرد که در همان سمت رودخانه است. او از کدام نقطه از ساحل آب بردارد که مسافتی که در مجموع طی می کند، کمترین حالت ممکن باشد؟»

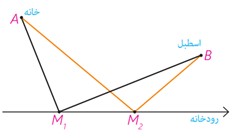
مسئله، پیدا کردن نقطهٔ M روی خط d است به گونه ای که AM+MB کمترین مقدار ممکن باشد.

هرون ابتدا بازتاب A را نسبت به خط پیدا کرد و آن را 'A نامید. خط فرضی A’B خط بازتاب را در نقطه ای مثل M قطع می کند. او مدعی شد که M جواب مسئله است و AM+MB کوتاه ترین مسیر ممکن است.

با هم دلیل ادعای هرون را بررسی می کنیم:

1- برای هر نقطهٔ دلخواه دیگری نظیر M₁ داریم 'M₁A=M₁A (و به همین ترتیب AM=A’M)؛ چرا؟

زیرا با توجه به تعریف بازتاب خط d عمود منصف پاره خط AA’ است و نقاط M و M₁ روی این خط هستند. بنا بر خاصیت عمود منصف AM=A’M و M₁A=M₁A’

2 در مثلث A’M₁B داریم \(A'{M_1} + {M_1}B > A'B\)؛ چرا؟

از تساوی A’B=A’M+MB و (1) و (2) ادعای هرون را اثبات کنید.

بنا بر قضیه نامساوی مثلث، در هر مثلث مجموع دو ضلع از ضلع سوم بزرگتر است.

\(\begin{array}{l}A'B = A'M + MB\;\mathop \Rightarrow \limits^{A'M = AM} \;A'B = AM + MB\\\\\left. \begin{array}{l}A'B = AM + MB\\A'B < A'{M_1} + {M_1}B\end{array} \right\} \Rightarrow AM + MB < A'{M_1} + {M_1}B\end{array}\)

و چون نقطه M₁ دلخواه بود، پس ادعای هرون اثبات می شود.