جواب سؤال متن صفحه 52 درس 2 هندسه یازدهم (تبدیل های هندسی و کاربردها)
تعداد بازدید : 84.73Mپاسخ سؤال متن صفحه 52 هندسه یازدهم
-گام به گام سؤال متن صفحه 52 درس تبدیل های هندسی و کاربردها
-سؤال متن صفحه 52 درس 2
-شما در حال مشاهده جواب سؤال متن صفحه 52 هندسه یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
سوال: در روش هرون نقطهٔ 'A طرف دیگر رودخانه قرار دارد. اگر در عمل به دنبال یافتن کوتاه ترین مسیر مورد نظر باشیم و امکان رفتن به طرف دیگر رودخانه نباشد، چگونه نقطۀ M را می توان پیدا کرد؟
(راهنمایی: از تشابه دو مثلث AHM و BH’M کمک بگیرید و توجه داشته باشید که اندازه های AH و 'BH دو مقدار معلوم هستند).
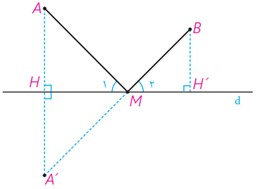
نقطه M روی عمود منصف AA’ است. بنابراین MA=MA’ پس مثلث MAA’ متساوی الساقین است. در نتیجه خط d نیمساز زاویه AMA’ است:
\(\left. \begin{array}{l}{\widehat M_1} = {\widehat M_3}\\{\widehat M_3} = {\widehat M_2}\end{array} \right\} \Rightarrow {\widehat M_1} = {\widehat M_2}\)
بنابراین:
\(\left. \begin{array}{l}{\widehat M_1} = {\widehat M_2}\\\widehat H = \widehat {H'}\end{array} \right\} \Rightarrow A'HM \sim BH'M\)
و چون دو مثلث AHM و A’HM با هم همنهشت هستند، داریم:
\(AHM \sim BH'M\)
در نتیجه نقطه M ، نقطه ای است که در آن \({\widehat M_1} = {\widehat M_2}\). زیرا:
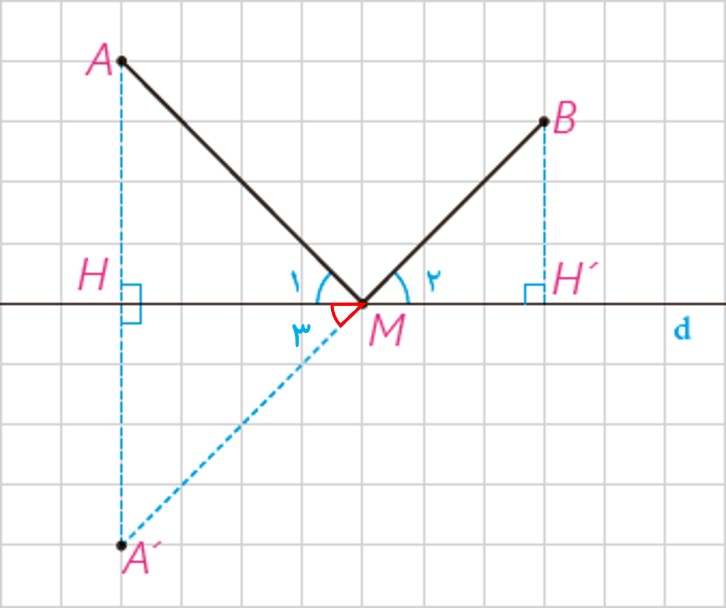
\(AM + MB = A'M + MB\)
ب دو شهر A و B مطابق شکل در یک طرف رودخانه ای واقع اند. می خواهیم جاده ای از A به B بسازیم به طوری که 4 کیلومتر از این جاده در ساحل رودخانه ساخته شود. این 4 کیلومتر را در چه قسمتی از رودخانه بسازیم تا مسیر ACDB کوتاه ترین مسیر ممکن باشد؟
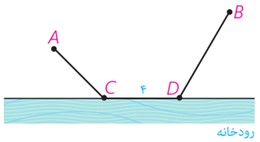
حل: مسئله را در چند مرحله حل می کنیم.
1 اگر جادهٔ ساحلی را از صورت مسئله حذف کنیم، به عبارتی اگر CD=0، این مسئله به کدام یک از مسائلی شبیه است که قبلاً دیده اید؟
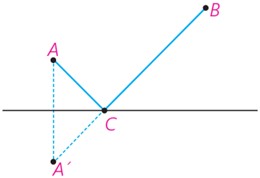
2 با توجه به شرایط مسئله، مسیر موردنظر، باید مسیری به شکل مسیر ACDB باشد؛ اما؛
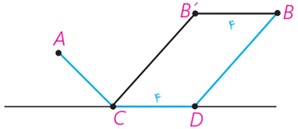
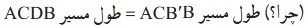
بنابراین:
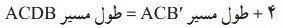
3 پس کافی است برای پیدا کردن کوتاه ترین مسیر ممکن به شکل ACDB مسیر را به گونه ای انتخاب کنیم که طول 'ACB کوتاهترین طول ممکن باشد.
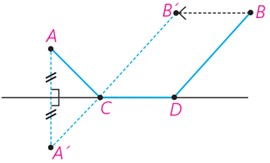
4 به کمک مراحل 1 تا 3 و شکل روبه رو توضیح دهید که رسم کوتاه ترین مسیر ACDB چگونه است.
1
مسئله هرون؛ مردی که می خواهد از رودخانه آب بردارد و به اصطبل ببرد.
2
در واقع نقطه C تحت بردار انتقالی به طول 4 به D منتقل شده و نقطه B’ نیز تحت همان بردار به B منتقل شده است. بنابراین با توجه به خواص تبدیل انتقال، چهارضلعی CDBB’ متوازی الاضلاع است؛ پس:
ACDB مسیر =
\(AC + CD + DB\;\;\mathop \Rightarrow \limits_{CB' = DB}^{CD = B'B} \;\;ACDB = AC + CB' + B'B\)
= ACB'B مسیر
3
ابتدا نقطه B را تحت بردار انتقالی به طول 4 و موازی رودخانه و در جهت شهر A به نقطه B’ انتقال می دهیم؛ حالا مسئله شبیه مسئله اصطبل می شود. بازتاب نقطه A را نسبت به کنار رودخانه بدست می آوریم، یعنی نقطه A’ . سپس از A’ به B’ وصل می کنیم تا نقطه C بدست آید. از نقطه C موازی رودخانه به سمت شهر B و به طول 4 حرکت می کنیم تا نقطه D بدست آید. به این ترتیب کوتاه ترین مسیر رسم می شود.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















