شاه کلید نکات
شاه کلید سوال
1
الف فرض کنید پاره خط ′A′B مجانس پاره خط AB در تجانس به مرکز O و نسبت k باشد؛ نشان دهید: \(\frac{{A'B'}}{{AB}} = \left| k \right|\) (نقطه O را خارج AB در نظر بگیرید).
ب اگر n ضلعی A’1 A’2 … A’n مجانس n ضلعی A1 A2 … An باشد، نشان دهید این دو n ضلعی با هم متشابه اند.
الف
1) در این حالت نقطه O روی پاره خط AB قرار دارد و 0>k . در نتیجه:
\(\begin{array}{l}A'B' = OA' + OB'\;\;\mathop \Rightarrow \limits_{OB' = \left| k \right|.OB}^{OA' = \left| k \right|.OA} \\\\A'B' = \left| k \right|.OA + \left| k \right|.OB = \left| k \right|\left( {OA + OB} \right) = \left| k \right|.AB\\\\ \Rightarrow A'B' = \left| k \right|.AB \Rightarrow \frac{{A'B'}}{{AB}} = \left| k \right|\end{array}\)
2) در این حالت نقطه O روی پاره خط AB قرار دارد و 0<k . در نتیجه:
\(\begin{array}{l}A'B' = OA' + OB'\;\;\;\mathop \Rightarrow \limits_{OB' = k.OB}^{OA' = k.OA} \;\;\\\\A'B' = k.OA + k.OB = k\left( {OA + OB} \right) = k.AB\\\\ \Rightarrow A'B' = k.AB \Rightarrow \frac{{A'B'}}{{AB}} = k\end{array}\)
3) در این حالت نقطه O روی امتداد پاره خط AB قرار دارد و 0>k . در نتیجه:
\(\begin{array}{l}A'B' = OA' - OB'\;\;\mathop \Rightarrow \limits_{OB' = \left| k \right|.OB}^{OA' = \left| k \right|.OA} \;\\\\A'B' = \left| k \right|.OA - \left| k \right|.OB = \left| k \right|\left( {OA - OB} \right) = \left| k \right|.AB\\\\ \Rightarrow A'B' = \left| k \right|.AB \Rightarrow \frac{{A'B'}}{{AB}} = \left| k \right|\end{array}\)
4) در این حالت نقطه O روی امتداد پاره خط AB قرار دارد و 0<k . در نتیجه:
\(\begin{array}{l}A'B' = OA' - OB'\;\;\;\mathop \Rightarrow \limits_{OB' = k.OB}^{OA' = k.OA} \\\\A'B' = k.OA - k.OB = k\left( {OA - OB} \right) = k.AB\\\\ \Rightarrow A'B' = k.AB \Rightarrow \frac{{A'B'}}{{AB}} = k\end{array}\)
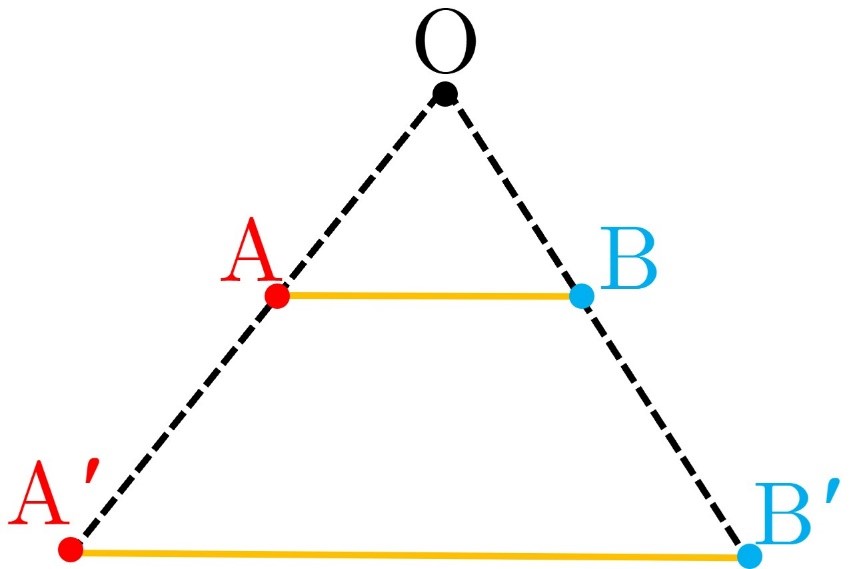
5) در این حالت نقطه O روی پاره خط AB قرار ندارد و 0>k . در نتیجه:
\(\begin{array}{l}\left. \begin{array}{l}OA' = \left| k \right|.OA\\OB' = \left| k \right|.OB\end{array} \right\} \Rightarrow \frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}}\\\\ \Rightarrow O\mathop A\limits^\Delta B \sim O\mathop {A'}\limits^\Delta B'\\\\ \Rightarrow \frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{A'B'}}{{AB}} = \left| k \right|\end{array}\)
\(\widehat {AOB} = \widehat {A'OB'}\)
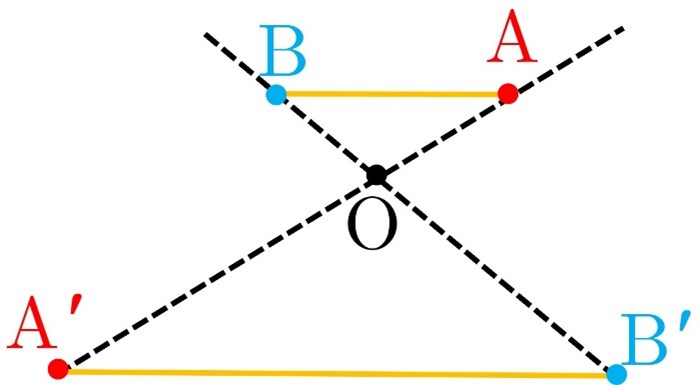
6) در این حالت نقطه O روی پاره خط AB قرار ندارد و 0<k . در نتیجه:
\(\left. \begin{array}{l}OA' = k.OA\\OB' = k.OB\end{array} \right\} \Rightarrow \frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = k \to AB\parallel A'B' \to \frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{A'B'}}{{AB}} = k\)
\(\widehat {AOB} = \widehat {A'OB'}\)
ب
فرض کنیم \({A_1}{A_2}{A_3} \cdots {A_n}\) یک n ضلعی و نقطه O مرکز تجانس و k نسبت تناسب باشد و چند ضلعی \({A'_1}{A'_2} \cdots {A'_n}\) مجانس آن باشد بنا بر تعریف تجانس داریم:
\(\begin{array}{l}\left. \begin{array}{l}O{{A'}_1} = k.O{A_1}\\O{{A'}_2} = k.O{A_2}\\O{{A'}_3} = k.O{A_3}\\ \vdots \\O{{A'}_n} = k.O{A_n}\end{array} \right\}\\\\ \Rightarrow \frac{{O{{A'}_1}}}{{O{A_1}}} = \frac{{O{{A'}_2}}}{{O{A_2}}} = \frac{{O{{A'}_3}}}{{O{A_3}}} = \cdots = \frac{{O{{A'}_n}}}{{O{A_n}}} = k\end{array}\)
پس چون اضلاع همه متناسب هستند بنا بر قضیه 3 تشابه نتیجه می گیریم این دو چند ضلعی متشابه اند.
2 با توجه به ویژگی های تجانس و به کمک مثال نقض نشان دهید دو شکل متشابه، الزاماً متجانس نیستند.
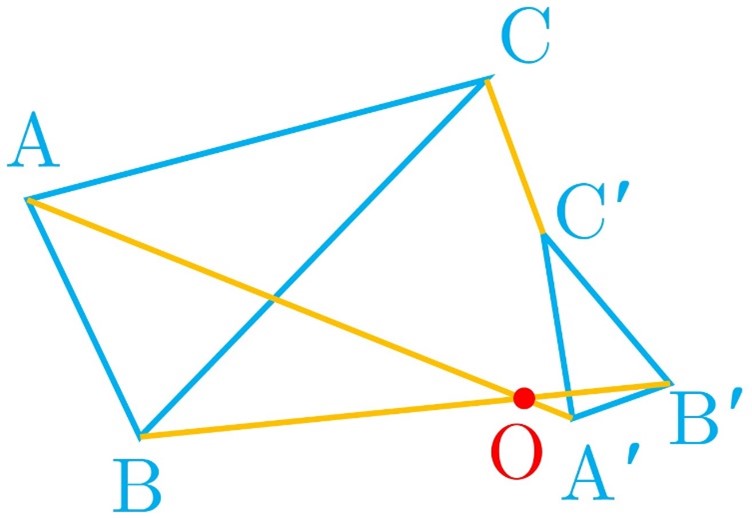
کافی است که دو شکل متشابه رسم کنیم که وقتی هر دو نقطه را به تصویرش وصل می کنیم و امتداد می دهیم، همرس نشوند . به این ترتیب مرکز تجانس وجود نخواهد داشت و در این صورت تجانسی هم در کار نیست. در شکل مقابل مثلث های ABC و A’B’C’ متشابه اند، اما متجانس نیستند.
1736019749.png)
