جواب تمرین صفحه 69 درس 2 حسابان یازدهم (تابع)
تعداد بازدید : 86.34Mپاسخ تمرین صفحه 69 حسابان یازدهم
-گام به گام تمرین صفحه 69 درس تابع
-تمرین صفحه 69 درس 2
-شما در حال مشاهده جواب تمرین صفحه 69 حسابان یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 اگر f(x)=2x و g(x)=2-x، توابع \(\frac{f}{g}\) ، f-g و fog را به همراه دامنهٔ آنها به دست آورید.
\(\begin{array}{l}{D_f} = \mathbb{R}\\{D_g} = \mathbb{R}\\\\\frac{f}{g}\left( x \right) = \frac{{4x}}{{x - 2}} \Rightarrow {D_{\frac{f}{g}}} = {D_f} \cap {D_g} - \left\{ {x\left| {g\left( x \right) = 0} \right.} \right\} \\= \mathbb{R} - \left\{ 2 \right\}\\\\\left( {f - g} \right)\left( x \right) = 5x + 2 \Rightarrow {D_{f - g}} = {D_f} \cap {D_g} = \mathbb{R}\\\\fog\left( x \right) = f\left( {g\left( x \right)} \right) = 4\left( {2 - x} \right) = - 4x + 8\\ \\\Rightarrow {D_{fog}} = \left\{ {x \in {D_g}\left| {g\left( x \right) \in {D_f}} \right.} \right\} \\= \left\{ {x \in \mathbb{R}\left| {\left( {2 - x} \right) \in \mathbb{R}} \right.} \right\} = \mathbb{R}\end{array}\)
2 برای دو تابع \(f\left( x \right) = \frac{1}{{x - 3}}\) و \(g\left( x \right) = \frac{4}{x}\) تابع fog و دامنهٔ آن را به دست آورید.
\(\begin{array}{l}{D_f} = \mathbb{R} - \left\{ 3 \right\}\quad :x \ne 3\\{D_g} = \mathbb{R} - \left\{ 0 \right\}\;\quad :x \ne 0\\fog\left( x \right) = f\left( {g\left( x \right)} \right) = f\left( {\frac{4}{x}} \right) = \frac{1}{{\frac{4}{x} - 3}} = \frac{x}{{4x - 3}}\\{D_{fog}} = \left\{ {x \in {D_g}\left| {g\left( x \right) \in {D_f}} \right.} \right\} = \\\left\{ {x \ne 0\left| {\frac{4}{x} \ne 3} \right.} \right\} = \left\{ {x \ne 0\left| {x \ne \frac{3}{4}} \right.} \right\} = \mathbb{R} - \left\{ {0\;,\;\frac{3}{4}} \right\}\end{array}\)
3 کدام یک از گزاره های زیر درست و کدام یک نادرست است؟
الف اگر g(4)=7 و f(7)=5 آنگاه \((fog)(4)=35\)
ب اگر f(x)=x+4 و g(x)=3x آنگاه \(\left( {\frac{f}{g}} \right)\left( 2 \right) = 1\)
پ اگر g(x)=2x-1 و \(f\left( x \right) = \sqrt x \) آنگاه \((fog)(5)=g(2)\)
ت برای هر دو تابع f و g داریم: fog=gof
ث اگر \(f\left( x \right) = {x^2} - 4\) و \(g\left( x \right) = \sqrt {{x^2} - 4} \) ، آنگاه 25-=(5)(fog) و \(\left( {fog} \right)\left( x \right) = - {x^2}\)
ج برای هر دو تابع f و g داریم: fg=gf
الف نادرست
ب درست
پ درست
ت نادرست
ث نادرست
ج درست
4 فرض کنیم \(\left\{ \begin{array}{l}g:N \to N\\g\left( n \right) = 2n\end{array} \right.\) و \(f:A \to N\) به این صورت تعریف شود: \(f = \left\{ {\left( {1,2} \right)\;,\;\left( {2,3} \right)\;,\;\left( {3,5} \right)\;,\;\left( {4,7} \right)} \right\}\) که در آن: {A={1,2,3,4، توابع f+g و gof را به دست آورید.
\(\begin{array}{l}{D_f} = A\\{D_g} = \mathbb{N}\\{D_{f + g}} = {D_f} \cap {D_g} = A\\ \Rightarrow f + g = \left\{ {\left( {1\;,\;2 + 2} \right)\;,\;\left( {2\;,\;3 + 4} \right)\;,\;\left( {3\;,\;5 + 6} \right)\;,\;\left( {4\;,\;7 + 8} \right)} \right\}\\ = \left\{ {\left( {1\;,\;4} \right)\;,\;\left( {2\;,\;7} \right)\;,\;\left( {3\;,\;11} \right)\;,\;\left( {4\;,\;15} \right)} \right\}\\{D_{gof}} = \left\{ {x \in {D_f}\left| {f\left( x \right) \in {D_g}} \right.} \right\} = \left\{ {x \in A\left| {f\left( x \right) \in \mathbb{N}} \right.} \right\} = A\\ \Rightarrow gof = \left\{ {\left( {1\;,\;4} \right)\;,\;\left( {2\;,\;6} \right)\;,\;\left( {3\;,\;10} \right)\;,\;\left( {4\;,\;14} \right)} \right\}\end{array}\)
5 اگر \(f = \left\{ {\left( { - 4,13} \right),\left( { - 1,7} \right),\left( {0,5} \right),\left( {\frac{5}{2},0} \right),\left( {3, - 5} \right)} \right\}\) و \(g = \left\{ {\left( { - 4, - 7} \right),\left( { - 2, - 5} \right),\left( {0, - 3} \right),\left( {3,0} \right),\left( {5,2} \right),\left( {9,6} \right)} \right\}\) توابع f+g و f-g و \(\frac{f}{g}\) را به دست آورید.
\(\begin{array}{l}f + g = \left\{ {\left( { - 4\;,\;6} \right)\;,\;\left( {0\;,\;2} \right)\;,\;\left( {3\;,\; - 5} \right)} \right\}\\f - g = \left\{ {\left( { - 4\;,\;20} \right)\;,\;\left( {0\;,\;8} \right)\;,\;\left( {3\;,\; - 5} \right)} \right\}\\\frac{f}{g} = \left\{ {\left( { - 4\;,\; - \frac{{13}}{7}} \right)\;,\;\left( {0\;,\; - \frac{5}{3}} \right)} \right\}\end{array}\)
6 اگر \(f\left( x \right) = \sqrt {{x^2} + 5} \) و \(g\left( x \right) = \sqrt {4 - {x^2}} \) ، دامنه و ضابطهٔ توابع fog و gof را به دست آورید.
\(\begin{array}{*{20}{l}}{{D_f} = \mathbb{R}}\\{{D_g} = \left[ { - 2\,,\,2} \right]}\\{}\\\begin{array}{l}{D_{fog}} = \left\{ {x \in {D_g}\left| {g\left( x \right) \in {D_f}} \right.} \right\}\\\\ = \left\{ {x \in \left[ { - 2\,,\,2} \right]\left| {\sqrt {4 - {x^2}} \: \in \mathbb{R}} \right.} \right\} = \left[ { - 2\,,\,2} \right]\end{array}\\\begin{array}{l}\\fog\left( x \right) = f\left( {g\left( x \right)} \right) = f\left( {\sqrt {4 - {x^2}} } \right)\\\\ = \sqrt {{{\left( {\sqrt {4 - {x^2}} } \right)}^2} + 5} \: = \sqrt {9 - {x^2}} \end{array}\\{}\\\begin{array}{l}{D_{gof}} = \left\{ {x \in {D_f}\left| {f\left( x \right) \in {D_g}} \right.} \right\}\\\\ = \left\{ {x \in \mathbb{R}\left| {\sqrt {{x^2} + 5} \: \in \left[ { - 2\,,\,2} \right]} \right.} \right\}\end{array}\\\begin{array}{l}\\ = \left\{ {x \in \mathbb{R}\left| {x \notin \mathbb{R}} \right.} \right\} = \emptyset \end{array}\\\begin{array}{l}\\\sqrt {{x^2} + 5} \: \in \left[ { - 2\,,\,2} \right]\,:\, - 2 \le \sqrt {{x^2} + 5} \: \le 2\\\\ \Rightarrow 0 \le \sqrt {{x^2} + 5} \: \le 2\end{array}\\\begin{array}{l}\\ \Rightarrow 0 \le {x^2} + 5 \le 4 \Rightarrow \: - 5 \le {x^2} \le \: - 1\,\, \otimes \end{array}\\\begin{array}{l}\\gof\left( x \right) = g\left( {f\left( x \right)} \right) = g\left( {\sqrt {{x^2} + 5} } \right)\end{array}\\\begin{array}{l}\\ = \sqrt {4 - {{\left( {\sqrt {{x^2} + 5} } \right)}^2}} \: = \sqrt { - 1 - {x^2}} \,\, \otimes \end{array}\end{array}\)
7 اگر \(f\left( x \right) = {x^2} - 9\) و g(x)=x+3، ضابطۀ \(\frac{f}{g}\) و دامنهٔ آن در ادامه محاسبه شده اند. چه اشتباهی در محاسبه رخ داده است؟
\(\frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{{x^2} - 9}}{{x + 3}} = \frac{{\left( {x - 3} \right)\left( {x + 3} \right)}}{{x + 3}} = x - 3\;\;\;,\;\;\;{D_{\frac{f}{g}}} = R\)
دامنه تقسیم قبل از ساده شدن محاسبه می شود؛ در نتیجه:
\(\begin{array}{l}{D_f} = \mathbb{R}\\{D_g} = \mathbb{R}\\{D_{\frac{f}{g}}} = {D_f} \cap {D_g} - \left\{ {x\left| {g\left( x \right) = 0} \right.} \right\} = \mathbb{R} - \left\{ { - 3} \right\}\end{array}\)
8 اگر f(x)=2x+5 رابطه های f-1(x) و fof-1 و f-1of را به دست آورید.
\(\begin{array}{*{20}{l}}{f\left( x \right) = 2x + 5}\\\begin{array}{l}\\y = 2x + 5 \Rightarrow 2x = y - 5 \Rightarrow x = \frac{{y - 5}}{2}\end{array}\\\begin{array}{l}\\ \Rightarrow {f^{ - 1}}\left( y \right) = \frac{{y - 5}}{2}\end{array}\\\begin{array}{l}\\ \Rightarrow {f^{ - 1}}\left( x \right) = \frac{{x - 5}}{2}\end{array}\\\begin{array}{l}\\fo{f^{ - 1}}\left( x \right) = f\left( {{f^{ - 1}}\left( x \right)} \right) = \end{array}\\\begin{array}{l}\\f\left( {\frac{{x - 5}}{2}} \right) = 2\left( {\frac{{x - 5}}{2}} \right) + 5 = x\end{array}\\\begin{array}{l}\\{f^{ - 1}}of\left( x \right) = {f^{ - 1}}\left( {f\left( x \right)} \right) = \end{array}\\\begin{array}{l}\\{f^{ - 1}}\left( {2x + 5} \right) = \frac{{\left( {2x + 5} \right) - 5}}{2} = x\end{array}\end{array}\)
9 نمودار تابع f و g داده شده اند. ضابطه f+g، f-g و fg را محاسبه کنید.
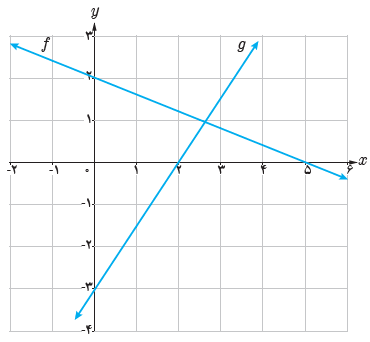
\(\begin{array}{l}f\left( x \right) = - \frac{2}{5}x + 2\\g\left( x \right) = \frac{3}{2}x - 3\\\left( {f + g} \right)\left( x \right) = f\left( x \right) + g\left( x \right) = \frac{{11}}{{10}}x - 1\\\left( {f - g} \right)\left( x \right) = f\left( x \right) - g\left( x \right) = - \frac{{19}}{{10}}x + 5\\\left( {f.g} \right)\left( x \right) = f\left( x \right).g\left( x \right) = - \frac{3}{5}{x^2} + \frac{{21}}{5}x - 6\end{array}\)
10 با توجه به نمودار مقابل، هرکدام از عبارت های داده شده را در صورت امکان محاسبه کنید.
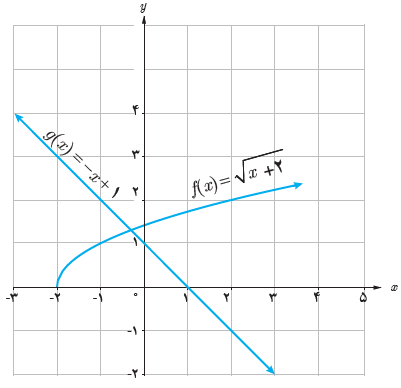
الف (2)(f + g)
ب (3)(f + g)
پ \(\left( {fg} \right)\left( {\frac{1}{2}} \right)\)
ت (4-)(fog)
ث \(\left( {\frac{f}{g}} \right)\left( 0 \right)\)
ج (1-)(gof)
الف
\(\left( {f + g} \right)\left( 2 \right) = f\left( 2 \right) + g\left( 2 \right) = 2 + 1 = 3\)
ب
\(\left( {f + g} \right)\left( { - 3} \right) = f\left( { - 3} \right) + g\left( { - 3} \right) = \otimes\)
پ
\(\left( {fg} \right)\left( {\frac{1}{2}} \right) = f\left( {\frac{1}{2}} \right)g\left( {\frac{1}{2}} \right) = \sqrt {\frac{5}{2}} \times \frac{1}{2} = \frac{{\sqrt {10} }}{4}\)
ت
\(\left( {fog} \right)\left( { - 4} \right) = f\left( {g\left( { - 4} \right)} \right) = f\left( 5 \right) = \sqrt 7\)
ث
\(\left( {\frac{f}{g}} \right)\left( 0 \right) = \frac{{f\left( 0 \right)}}{{g\left( 0 \right)}} = \frac{{\sqrt 2 }}{1} = \sqrt 2\)
ج
\(\left( {gof} \right)\left( { - 1} \right) = g\left( {f\left( { - 1} \right)} \right) = g\left( 1 \right) = 0\)
11 نشان دهید که وارون (معکوس) هر تابع خطی به صورت y=ax+b (a≠0) باز هم یک تابع خطی است.
\(\begin{array}{*{20}{l}}{f\left( x \right) = ax + b \Rightarrow y = ax + b \Rightarrow y - b = ax}\\\begin{array}{l}\\ \Rightarrow x = \frac{{y - b}}{a} = \frac{1}{a}y - \frac{b}{a} = a'y + b'\end{array}\\\begin{array}{l}\\ \Rightarrow {f^{ - 1}}\left( y \right) = a'y + b' \Rightarrow {f^{ - 1}}\left( x \right) = a'x + b'\end{array}\\{}\\{f\left( x \right) = ax + b \Rightarrow {f^{ - 1}}\left( x \right) = a'x + b'}\end{array}\)
12 تابع \(f\left( x \right) = \frac{5}{9}\left( {x - 32} \right)\) درجه فارنهایت را به درجه سانتی گراد تبدیل می کند. تابعی بنویسید که درجه سانتی گراد را به عنوان ورودی دریافت کند و درجه فارنهایت را به عنوان خروجی تحویل دهد.
\(\begin{array}{l}f\left( x \right) = \frac{5}{9}\left( {x - 32} \right) \Rightarrow y = \frac{5}{9}\left( {x - 32} \right)\\ \Rightarrow \frac{9}{5}y = x - 32 \Rightarrow x = \frac{9}{5}y + 32\\ \Rightarrow {f^{ - 1}}\left( y \right) = \frac{9}{5}y + 32 \Rightarrow {f^{ - 1}}\left( x \right) = \frac{9}{5}x + 32\end{array}\)
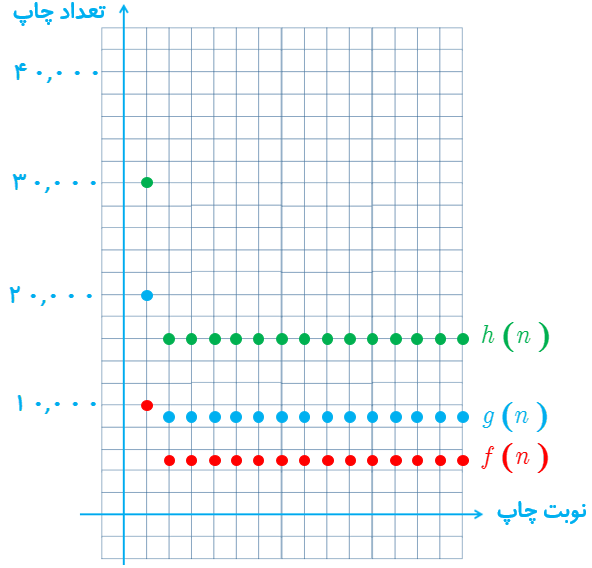
13 در تصاویر زیر طرح جلد چند کتاب پرفروش در حوزهٔ خاطرات دفاع مقدس را می بینید:
یکی از این کتاب ها در چاپ اول ١٠ هزار نسخه و در هر یک از چاپ های دیگر 7 هزار نسخه تولید شده است.
کتاب دیگر در چاپ اول ٢٠ هزار نسخه و در هر یک از چاپ های بعدی 9 هزار نسخه به چاپ رسیده است.
الف تابع هایی بنویسید که تعداد نسخه های چاپ شده هر یک از این دوکتاب را برحسب شماره چاپ نمایش دهند.
ب تابعی بنویسید که مجموع نسخه های چاپ شدهٔ هر دو کتاب را نمایش دهد.
پ نمودار هر سه تابع را در یک دستگاه محورهای مختصات رسم کنید.
الف
\(\begin{array}{l}f\left( n \right) = \left\{ \begin{array}{l}10,000\quad ,n = 1\\7,000\quad \;,n > 1\end{array} \right.\\g\left( n \right) = \left\{ \begin{array}{l}20,000\quad ,n = 1\\9,000\quad \;,n > 1\end{array} \right.\end{array}\)
ب
\(h\left( n \right) = f\left( n \right) + g\left( n \right) = \left\{ \begin{array}{l}30,000\quad ,n = 1\\16,000\quad \;,n > 1\end{array} \right.\)
ت
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















